ТЕМА 1.10. АНАЛИТИЧЕСКОЕ СЧИСЛЕНИЕ ПУТИ СУДНА. ОЦЕНКА ТОЧНОСТИ СЧИСЛЕНИЯ И ЕЕ УЧЕТ ДЛЯ ОБЕСПЕЧЕНИЯ БЕЗОПАСНОСТИ ПЛАВАНИЯ.
АНАЛИТИЧЕСКОЕ (ПИСЬМЕННОЕ) СЧИСЛЕНИЕ
КООРДИНАТ СУДНА
Сущность и основные формулы аналитического
(письменного) счисления
Кроме графического счисления пути судна, учет его плавания может производиться с помощью аналитического (письменного) счисления.
Аналитическое счисление – вычисление географических координат судна по его курсу и плаванию (по сделанным судном разностям широт и долгот) по формулам вручную или с помощью счетно-решающих устройств.
Аналитическое счисление производится по формулам и применяется при плавании судна вдали от берегов на океанских переходах, когда ведение графического счисления становится неточным из-за больших погрешностей в графических построениях на морских навигационных картах мелкого масштаба.
Чаще всего аналитическое счисление применяется:
- ’ при непрерывной выработке текущих счислимых координат места судна, вводимых в системы судовой автоматики. Задача решается с помощью автоматических счетно-решающих устройств (или ЭВМ);
- ’ при периодическом вычислении счислимых координат места судна в тех случаях, когда необходимо исключить погрешности счисления за счет неточности графических построений, связанных с прокладкой пути судна на мелкомасштабной карте. Задача решается вручную или с помощью счетно-решающих устройств (для контроля точности графических построений на карте; определения места судна по разновременным наблюдениям светил).
Аналитическое счисление с помощью автоматических счетно-решающих устройств производится по формулам с учетом сжатия Земли. В простейших системах решаются формулы без учета сжатия Земли.
Получим основные формулы аналитического счисления (рис. 17.1).
Судно из точки А (j1 l1), следуя постоянным курсом (К) по локсодромии, пришло в точку В (j2 l2).
Если будут известны сделанные судном разность широт (РШ) и разность долгот (РД) то координаты точки В (j2 l2) легко получить из соотношений:
 (17.1)
(17.1)

Рис. 17.1. Аналитическое (письменное) счисление пути судна
Значение разности широт (РШ) и разности долгот (РД) можно рассчитать по известным элементам движения: К ® курсу судна и S ® плаванию судна по этому курсу.
Считая Землю за сферу (шар) из элементарно малого треугольника Аа¢в¢:
 ® приращение широты;
® приращение широты;
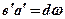 ® приращение отшествия;
® приращение отшествия;
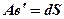 ® приращение расстояния,
® приращение расстояния,
где  – разность широт (мили);
– разность широт (мили);
 – расстояние между меридианами по параллели от т. а¢ до т. в¢ – отшествие(мили);
– расстояние между меридианами по параллели от т. а¢ до т. в¢ – отшествие(мили);
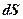 – плавание судна по локсодромии между точкой А и точкой в¢ (мили).
– плавание судна по локсодромии между точкой А и точкой в¢ (мили).
Если D Аа¢в¢ принять за плоский, можно написать дифференциальные уравнения:
 (17.2)
(17.2)
В результате интегрирования значений  и
и  при K = const, получим:
при K = const, получим:
1) ª 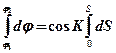
то есть
 (17.3)
(17.3)
2) ª 
то есть 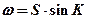 . (17.4)
. (17.4)
Для вычисления значения разности долгот – РД, воспользуемся соотношением между длиной дуги экватора и параллели:
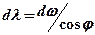
Умножим числитель (  ) и знаменатель (cos j) на
) и знаменатель (cos j) на  , тогда
, тогда

так как из D Аа¢в¢

то 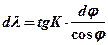 .
.
Решение этого уравнения приводит к известному интегралу:

а 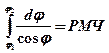 ,
,
тогда 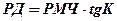 . (17.5)
. (17.5)
Для вывода прямой связи между отшествием (ОТШ) и разностью долгот (РД), используем теорему о среднем значении интеграла, которая дает:

где jn – промежуточное значение широты в интервале между j1 и j2.
Тогда для разности долгот – РД можно написать
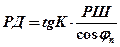 (17.6)
(17.6)
Приравняв оба значения разности долгот (РД), полученного по формулам (17.5) и (17.6), получим значение промежуточной широты jn:
 (17.7)
(17.7)
откуда 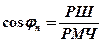 . (17.8)
. (17.8)
Подставив значение соs jn (формула 17.8) в формулу (17.6) для разности долгот (РД) и учтя, что
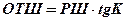 , (17.9)
, (17.9)
окончательно получим:
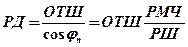 (17.10)
(17.10)
где отшествие (ОТШ) и разность широт (РШ) в милях.
Таким образом отшествие (ОТШ) представляет собой длину параллели (в милях) между меридианами точек А и В, широта которой (параллели) определяется соотношением
 . (17.11)
. (17.11)
На практике, при ведении аналитического учета на коротких расстояниях, можно допустить, что в интервале от j1 до j2 значение cos j изменяется линейно, тогда
 (17.12)
(17.12)
и приближенная формула для расчета разности долгот – РД примет вид:
 (17.13)
(17.13)
то есть разность долгот (РД) равна отшествию (ОТШ), деленному на косинус средней широты ( 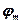 ).
).
По формулам (17.3) и (17.4) составлены таблица 24 «МТ-75» (с. 260¸272) и таблица 2.19а «МТ-2000» (с. 282¸294) «Разность широт и отшествие». В этих таблицах по плаванию S (от 0 до 100 миль) и курсу (через 1°) можно получить готовые значения разности широт (РШ) и отшествия (ОТШ), величины которых даны в таблице до сотых долей мили и поэтому могут быть использованы для плаваний (S) в 10 и 100 раз больших (или меньших) ® переносом запятой ® см. табл. 17.8.
Пример: 1) S = 450 миль, К = 37°, РШ = 359,4 мили к N и ОТШ = 270,8 мили к Е;
2) К = 230°, S = 1860 миль, РШ = 1195,6¢ к S и ОТШ = 1424,8¢ к W (см. табл. 17.1).
В «МТ-75» помещена также специальная таблица 25а «Разность долгот» (с. 273¸278) составленная по формуле (17.13).
Аналогичная таблица 2.20 – см. «МТ-2000» (с. 296¸301).
Разность широт и отшествие
(с. 271 «МТ-75» или с. 293 «МТ-2000»)
Таблица 17.1
| Плавание | ОТШ | РШ |
| 100 +(1000) 86 (860) | 76,60 + (766,0) 65,88 (658,8) | 64,28 + (642,8) 55,28 (552,8) |
| S S = 1860 миль | S ОТШ = 142,48 = (1424,8¢) | S РШ =119,56 = (1195,6¢) |
| 230° |
Входные аргументы:1) ОТШ = 1, 2, 3,…9 и 100 миль;
2) jm = 0¸86° через 0,1°.
Получение значений разности долгот (РД) для десятков или сотен миль значений отшествия (ОТШ) делается простым переносом запятой, отделяющей целую часть от дробной в найденных табличных значениях.
Пример 1. Найти значение разности долгот (РД), если j1 = 60°N, j2 = 20°N и отшествие – ОТШ = 246¢ к W.
Решение:
1)  .
.
2) ОТШ = 246¢ = 100 + 100 + 40 + 6.
По значениям 100, 100, 40 и 6 для jСР = 40° из табл. 25а «МТ-75» (с. 273) или табл. 2.20 «МТ-2000» (с. 296) выбираем значения разности долгот (см. табл. 17.2):
Таблица 17.2.
| ОТШ | РД1 |
| 100¢ 100¢ 40¢ 6¢ | 130,5¢ 130,5¢ 52,2¢ 7,8¢ |
| S ОТШ = 246¢ | S РД = 321,0¢ к W |
Ответ:РД = 321,0¢ к W.
Пример 2. По данным примера 1 найти значение разности долгот (РД), используя промежуточную широту (jn).
Решение:
- ž Находим значение jn (см. ф. 17.8).
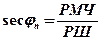 (17.14)
(17.14)
j1 = 60°N …. МЧ1 = 4507,4¢
j2 = 20°N…. МЧ2 = 1217,3¢
Значения меридиональных частей (МЧ1 и МЧ2) выбираем из табл. 26 «МТ-75» (с. 280¸287) или табл. 2.28а «МТ-2000» (с. 314¸321) ® табл. 24.5.
Из табл. 27 «МТ-75» (с. 288) или табл. 2.28б «МТ-2000» (с. 322) «Поправки для получения меридиональных частей шара» выбираем поправки для перехода к меридиональным частям (МЧ1, МЧ2) на шаре (в навигационных задачах Землю принимают за шар).
DМЧ1 = +20,0¢ (для j1 = 60°) и DМЧ2 = +7,8¢ (для j2 = 20°)
В результате: 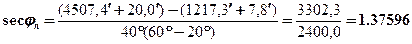
и  (см. табл. 6а «МТ-75» (с. 156¸199) или табл. 5.42а «МТ-2000» (с. 460) «Натуральные значения тригонометрических функций»® табл. 24.6.
(см. табл. 6а «МТ-75» (с. 156¸199) или табл. 5.42а «МТ-2000» (с. 460) «Натуральные значения тригонометрических функций»® табл. 24.6.
2)ž Разбиваем значение отшествия – ОТШ = 246¢ = 100 + 100 + 40 + 6 и выбираем соответствующие им (100, 100, 40, 6) значения разности долгот – РД из табл. 25а «МТ-75» или 2.20 «МТ-2000», интерполированием между jn = 43° и jn = 43,5° (см. табл. 17.3).
Таблица 17.3.
| ОТШ | РД2 |
| 100¢ 100¢ 40¢ 6¢ | 137,66¢ 137,66¢ 55,02¢ 8,26¢ |
| S ОТШ = 246¢ | S РД = 338,6¢ к W |
Сравнивая значение разности долгот из табл. 17.2 (РД1 = 321,0¢ к W) и значение разности долгот из табл. 17.3 (РД2 = 338,6¢ к W) видно (D = 17,6¢), что при больших значениях разности широт (РШ), нужно пользоваться не средним значением широты (jСР), а значением промежуточной широты (jПР).
Дата добавления: 2016-02-27; просмотров: 2025;
