Общие понятия и способы прогноза синоптического положения
Синоптический метод составления краткосрочных прогнозов базируется на прогнозе синоптического положения, прогнозе условий погоды и учете местных особенностей.
Под синоптическим положением понимается отображенная на картах погоды совокупность синоптических объектов, выявленных в результате измерения характеристик воздуха и оценивания погодных явлений, определяющих состояние атмосферных процессов в фиксированный момент времени.
Прогноз синоптического положения заключается в прогностических оценках перемещения и эволюции синоптических объектов, полученных на основе анализа состояния атмосферных процессов, отображенных на картах погоды. Этот прогноз играет вспомогательную роль, являясь первым подготовительным этапом и основой прогноза метеорологических факторов и величин. Каждому синоптическому объекту присущи определенные характерные типы погоды. Поэтому предсказания синоптического положения и его изменения являются прогнозами общего характера погоды в заданном районе.
Прогноз условий погоды неразрывно связан с прогнозом синоптического положения. Следует учитывать, что прогноз синоптического положения охватывает лишь крупномасштабные процессы, поэтому при прогнозе условий погоды обязательно необходимо учитывать местные особенности развития атмосферных процессов. При прогнозе условий погоды, кроме прогнозов синоптического положения, используются способы расчета ожидаемых количественных характеристик метеорологических величин, учитывается время года и время суток.
Местные условия (особенности) могут существенно влиять на погоду, особенно на образование туманов, грозовых явлений, заморозков и т.п.
Прогноз синоптического положения обычно оформляется графически путем составления прогностических карт погоды, которые затем являются основой для прогноза условий погоды и учета местных условий.
Способы прогноза синоптического положения условно делятся на следующие группы:
- численные методы, основанные на решении уравнений гидродинамики и термодинамики или на использовании методов теории вероятностей и математической статистики;
- приемы формальной и физической экстраполяции, не требующие применения сложной вычислительной техники;
- качественно-физические заключения синоптика об ожидаемом течении атмосферных процессов.
Поскольку ни один из перечисленных способов не обеспечивает достаточной точности прогностических оценок, то в оперативной работе используются все способы, применение которых является целесообразным, т.е., прогноз синоптического положения является комплексным прогнозом.
Перечисленные способы прогнозирования имеют много общего. Прежде всего, они имеют общую синоптическую основу. Все эти способы опираются на знании определенных закономерностей атмосферных процессов и обобщают опыт прогностической работы. Одной из начальных форм обобщения этого опыта являются эмпирические прогностические связи и правила.
Прогностические связи устанавливаются путем статистической обработки метеорологической информации, поэтому они получили название статистических закономерностей.
4.2. Численные методы
Гидродинамический метод прогноза погодынаправлен на расчет будущего барического поля, вертикальных токов и ветра, осадков, максимальной и минимальной температуры и других метеорологических величин с помощью численного решения уравнений гидродинамики и термодинамики.
Исходные основные уравнения гидродинамики, используемые для построения численного прогноза в системе координат х,у,р (р – атмосферное давление), выражают фундаментальные физические законы, сформулированные для сплошной среды: закон сохранения количества движения, закон сохранения массы и закон сохранения энергии.
Закон сохранения количества движения представлен уравнением движения в изобарической системе координат:

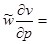 –g
–g  –lu, (4.1)
–lu, (4.1)
 –g
–g  lu, (4.2)
lu, (4.2)
где u,v,w – составляющие полного вектора скорости движения частицы;

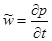 – эквивалент вертикальной составляющей скорости w
– эквивалент вертикальной составляющей скорости w 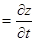 , взятой с обратным знаком;
, взятой с обратным знаком;
g – ускорение свободного падения;
H – геопотенциальная высота изобарической поверхности;
l = 2 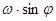 – параметр Кариолиса;
– параметр Кариолиса;
 – угловая скорость вращения Земли;
– угловая скорость вращения Земли;
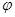 – географическая широта.
– географическая широта.
В левых частях выражений (4.1) и (4.2) записаны ускорения, приобретаемые частицей единичной массы, а в правых - силы, действующие на эту частицу. В свободной атмосфере силой турбулентного трения в силу ее малости можно пренебречь. Кроме того, можно пренебречь, как малыми, и вертикальными составляющими  и
и 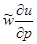 .
.
С учетом сделанных допущений уравнения (4.1) и (4.2) записываются в виде:

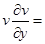 –
–  – lu (4.3)
– lu (4.3)

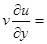 –
–  + lu
+ lu  (4.4)
(4.4)
Поскольку в крупномасштабных атмосферных процессах (с размерами около тысячи километров) ускорения по вертикали пренебрежимо малы, уравнение, выражающее закон сохранения количества движения по оси р, упрощается, принимая вид уравнения статики. Однако из этого не следует, что исключаются вертикальные движения воздуха. Они учитываются другими уравнениями. Запись уравнения температуры воздуха в виде:
 –
–  (4.5)
(4.5)
говорит лишь о том, что в данном случае пренебрегается ускорениями, обусловленными нарушением равновесия между силой тяжести и вертикальной составляющей силы барического градиента.
Прогностическая модель атмосферы, использующая уравнение статики, получается, таким образом, в квазистатическом приближении. Все применяемые схемы прогноза крупномасштабных процессов основываются на квазистатическом приближении. Система уравнений (4.3) – (4.5) называется квазистатической системой уравнений.
Закон сохранения массы для сплошной среды записывается в виде уравнения неразрывности. В системе координат х,у.р в уравнении неразрывности пропадает слагаемое, характеризующее изменение плотности, и оно приобретает вид:
 (4.6)
(4.6)
Из этого уравнения следует, что в системе координат х,у,р атмосферный воздух описывается как несжимаемая жидкость. Это допущение значительно упрощает расчеты.
Закон сохранения энергии выражается первым началом термодинамики: притекающая к воздушной частице тепловая энергия расходуется на нагрев воздуха и работу расширения.
Для не слишком больших промежутков времени (порядка одних суток) притоком тепла можно пренебречь. В этом случае уравнение притока тепла принимает вид:
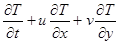 –
–  (4.7)
(4.7)
Модель атмосферного процесса, в которой используется уравнение (4.7), называется адиабатической моделью.
Принятие условия адиабатичности процессов значительно упрощает решение прогностической задачи и в то же время не вносит существенных ошибок.
Система уравнений (4.3 – 4.7) состоит из пяти уравнений и содержит пять неизвестных функций. Среди них три производные по времени:
( 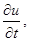

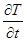 ),
),
кроме того, неизвестны изменяющиеся во времени высоты изобарических поверхностей Ни вертикальная скорость в изобарической системе 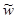 . Таким образом, имеется замкнутая система уравнений относительно функций и,v,T,H,
. Таким образом, имеется замкнутая система уравнений относительно функций и,v,T,H, 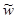 . В общем виде аналитически эта система не решается, поэтому решение ее производится численными методами.
. В общем виде аналитически эта система не решается, поэтому решение ее производится численными методами.
4.3. Экстраполяционные прогнозы
Дата добавления: 2016-02-24; просмотров: 1744;
