ПРОСТРАНСТВЕННЫЕ КООРДИНАТЫ
Теперь мы уже видим, что можем наблюдать широкий спектр объектов. Мы можем группировать их при заданном масштабе наблюдения на точки, линии, области и поверхности. И мы можем классифицировать их при помощи измерений их характеристик в четырех различных шкалах -номинальной, порядковой, интервалов, отношений — в зависимости от того, какое нам требуется описание, и как мы собираемся их сравнивать. Но знание
* Здесь невольно приравнялись слова "абсолютный" и "относительный". Дело в том, что шкала отношений действительно является абсолютной в том смысле, что ее начало имеет определенный физический ("абсолютный") смысл и не может быть установлено произвольно. Чтобы уменьшить путаницу, такая шкала называется не "относительной шкалой" а "шкалой отношений". Фундаментальное же различие всех четырех шкал обусловлено свойствами, которыми занимается абстрактная алгебра (специальный раздел высшей математики). Здесь же будет достаточно сказать, что каждой шкале измерений соответствует определенный набор допустимых операций с ее значениями — прим. перев.:
того, где объекты расположены, что они такое, и как мы можем измерять их, - это только начало описания нашего мира. Нам еще нужно узнать, как эти получившие координаты и численное выражение объекты взаимодействуют в пространстве, создавая общую картину, которую мы наблюдаем.
До настоящего момента мы говорили, что можемопределять местоположение объектов в пространстве. Это — первая важная пространственная идея, которая нам нужна. Но определение местоположения означает, что у нас должен быть некий механизм сообщения положения каждого наблюдаемого объекта. Первым типом такого механизма являетсяабсолютное местоположение (absolute location), дающее нам определенную фиксированную точку на поверхности Земли. Но прежде нам нужно иметь систему координат, в которой мы могли бы выражать это положение и которая имеет фиксированное соотношение с земной поверхностью, измеряемую нами.
Земля в первом приближении - сферический объект, с большими или меньшими отклонениями от этой формы. Если мы рассматриваем ее в целом, то обычно удобно считать ее строго сферической. На этой сфере мы можем использовать некоторуюсферическую систему координат (spherical grid system), подчиняющуюся правилам геометрии. Рассматриваемая система координат имеет два набора воображаемых линий (Рисунок 2.5).
Первый набор линий начинается со средней линии Земли, экватора. Эти линии называютсяпараллелями (parallels), поскольку они параллельны друг другу и опоясывают Землю с востока на запад. Экватору мы присваиваем начальное числовое значение 0. При движении как на север, так и на юг от экватора мы рисуем дополнительные параллели, пока не достигнем
| отношения | операции | номинальная | порядковая | интервалов | отношений |
| тождество | равно / не равно | есть | есть | есть | есть |
| порядок | равно / не равно | нет | есть | есть | есть |
| разность (абсолютная) | вычитание/ сложение | нет | нет | есть | есть |
| отношение | умножение на коэффициент, деление | нет | нет | нет | есть |
соответствующего полюса. Поскольку каждой такой линии соответствует угол с вершиной в центре Земли, один из лучей которого пересекает земную поверхность в точке, лежащей на этой линии, мы можем использовать для ее числового выражения соответствующееугловое расстояние (angular distance). Эта величина, называемаяширотой (latitude), проходит от срединной параллели,экватора (equator), до каждого полюса четверть полного круга, то есть от 0 до 90°.
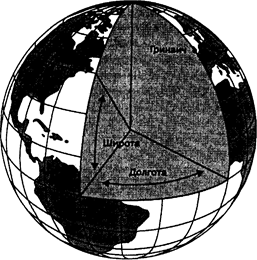
Рисунок 2.5. Географические координаты. Сферическая система координат с параллелями и меридианами. Параллели позволяют измерять угловое расстояние от экватора (0° широты) до 90° северной широты (Северный полюс) и до 90° южной широты (Южный полюс). Меридианы позволяют измерять угловое расстояние от начального меридиана (0°) до 180° восточной и 180° западной долготы, где проходит международная линия смены даты.
Это одна половина нашей координатной системы. Для завершения ее нам надо провести набор других линий, идущих точно перпендикулярно первым. Эти линии, называемые меридианами (meridians), идут от полюса до полюса. Отсчет их начинается сначального меридиана (prime meridian), проходящего через Гринвич, Англия. Если продолжить этот меридиан за полюса, то он превратится вмеждународную линию смены даты (international date line). От начального меридиана отсчитывается угловая величина, называемаядолготой (longitude), от 0 до 180° на запад, где проходит международная линия смены даты. Аналогично она отсчитывается и до 180е на восток, опять же, до международной линии смены даты.
Эта система угловых измерений позволяет нам обозначить абсолютное положение любой точки на земле простым указанием величин широты и долготы.
С ее помощью мы можем описать положение любого выбранного объекта. Вдобавок, эти угловые величины могут быть легко преобразованы в футы, мили, метры или километры, позволяя нам измерять большие и малые расстояния на земле, с использованием соответствующих формул. Хотя нам потребуется вносить некоторые коррективы в эту систему при создании плоских карт, задача которых - как можно точнее передать положения и взаимную ориентацию объектов на глобусе, тем не менее, это - достаточно изящная система для выражения абсолютного местоположения.
Однако по мере продолжения исследования нашего мира, мы скоро замечаем, что было бы очень полезно иметь возможность описывать не только абсолютные положения объектов, но и их отношения с другими объектами в географическом пространстве.

Рисунок 2.6. Расчет расстояния по дуге большого круга между двумя точками на сфере.
В действительности, этоотносительное местоположение становится весьма значимым для нашего географического анализа, когда относительное положение объекта влияет на его функционирование. Имея систему абсолютных координат, мы можем определить относительное положение простым вычитанием из больших координат меньших.
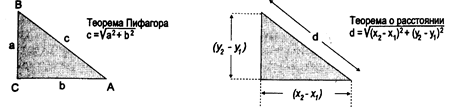
Рисунок 2.7. Вычисление расстояния на плоскости. Вычисление расстояния между двумя точками с использованием теоремы Пифагора и теоремы о расстоянии.
Конечно, относительное расстояние — только половина того, что нам хотелось бы знать. Было бы полезно знать также и направление. Например, мы могли бы сказать, что свалка находится в 1500 метрах на юго-восток от центра города. Это выражение расстояния и направления дает нам основу для описания точного положения свалки относительно города. Из теоремы Пифагора (Рисунок 2.7а) о соотношении сторон прямоугольного треугольника, мы можем определить длину гипотенузы через так называемую теорему о расстоянии (Рисунок 2.7b), которая выражается следующей формулой:
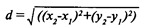
где
x2 - х1 = расстояние по оси Х или долготе у2 - у1 = расстояние по оси Y или широте* d = расстояние между двумя точками
Мы могли бы представить также и кое-какую дополнительную информацию, полезную для людей, живущих в городе. Если нам известно, что в этой местности преобладают ветры с северо-запада, мы могли бы сказать, что свалка находится на 1500 метров по ветру от города, показывая тем самым, что запах со свалки обычно не будет проблемой для горожан. Такой подход, хотя и менее строгий с точки зрения измерений, имеет также большое практическое применение. Это дает нам средство интерпретации того, что мы наблюдаем, определения значимых отношений между географическими объектами.
* В России распространена система координат 1942 г. для проекции Гаусса- Крюгера, в которой ось Х указывает на север, а ось Y - на восток.
Дата добавления: 2016-02-24; просмотров: 1386;
