ПРОСТРАНСТВЕННЫЕ ЭЛЕМЕНТЫ

Упражнение наших географических способностей начнем с рассмотрения типов объектов, с которыми нам предстоит иметь дело. Пространственные объекты реального мира можно разделить на легко идентифицируемые четыре типа: точки, линии, области и поверхности (Рисунок 2.1). Вместе они могут представлять большинство природных и социальных феноменов, которые мы встречаем каждый день. В рамках ГИС объекты реального мира явно представляются тремя типами объектов из указанных. Точки, линии и области могут представляться соответствующими символами, которые мы рассмотрим в Главе 3, поверхности же представляются чаще всего либо высотами точек, либо другими компьютерными средствами, которые мы рассмотрим в Главе 4. Сейчас же наиболее важно то, что в ГИС вся информация - явным образом пространственная. Феномены непространственные по своей природе (идеи, верования и др.) не могут непосредственно исследоваться в ГИС, если только им не присвоить некоторые представляющие их пространственные характеристики.

Процесс поиска пространственных представителей (spatial surrogates) сложен, и мы займемся им более детально несколько позднее. В настоящий момент мы ограничимся обсуждением более осязаемых форм географической информации.

Точечные объекты - это такие объекты, каждый из которых расположен только в одной точке пространства. По собственному опыту вы можете легко узнать такие объекты, как деревья, дома, перекрестки дорог, и многие другие. О таких объектах говорят, что онидискретные (discrete), в том смысле, что каждый из них может занимать в любой момент времени только определенную точку пространства. В целях моделирования считают, что у таких объектов нет пространственной протяженности, длины или ширины, но каждый из них может быть обозначен координатами своего местоположения. Говорят, что точки имеют нулевое количество пространственных измерений. В действительности, конечно, все точечные объекты имеют некоторую пространственную протяженность, пусть самую малую, иначе мы просто не смогли бы их увидеть. Мы принимаем отсутствие длины и ширины так, что, например, при измерениях атмосферного давления, характеризуемых потенциально бесконечным числом точек, сами точки всегда занимают определенные местоположения без каких-либо перекрытий. Масштаб, при котором мы наблюдаем эти объекты, задает рамки, определяющие представление этих объектов как точек. Например, если вы смотрите на дом с расстояния нескольких метров, сооружение выглядит внушительным и имеет существенные длину и ширину. Но это представление меняется, когда вы начинаете отдаляться: чем дальше, - тем меньше дом выглядит как площадной объект, тем больше - как точечный (Рисунок 2.2). Критерии выбора масштаба могут быть различными, если вы, например, собираетесь рассматривать расположение людей и мебели в доме, или если вас он интересует только в связи с другими домами, возможно с целым городом. В последнем случае дом может считаться точкой. Ваше наблюдение прошло через фильтр, в соответствии с тем, как вы хотите смотреть на объект.

Линейные объекты представляются как одномерные в нашем координатном пространстве. Такими "одномерными" объектами могут быть дороги, реки, границы, изгороди, любые другие объекты, которые существенно длинны и узки. Масштаб, при котором мы наблюдаем эти объекты, опять же, обусловливает порог, при пересечении которого мы можем считать их не имеющими ширины. Как вы знаете, реки, дороги, изгороди все имеют два измерения при близком рассмотрении. Но чем дальше мы от них, тем более тонкими они становятся. Постепенно они становятся такими тонкими, что оказывается невозможным представить их себе, как что-то иное, нежели линейные объекты, становится невозможным измерить их ширину (Рисунок 2.2). Другие линии, такие как политические границы, вообще не имеют ширины. В действительности, эти линии даже не являются материальными сущностями, а возникают как следствие политических соглашений. Несмотря на их неосязаемость, их можно, тем не менее, представлять как определенно пространственные, поскольку они разделяют две области географического пространства.

Рисунок 2.2. Влияние масштаба на размерность объектов.

Дома, видимые с близкого расстояния, имеют длину и ширину, но когда мы удаляемся, их измерения исчезают, оставляя впечатление о них как о точках.

Для линейных объектов, в отличие от точечных, мы можем указать пространственный размер простым определением их длины. Кроме того, поскольку они не занимают единственное местоположение в пространстве, мы должны знать, по меньшей мере, две точки - начальную и конечную -для описания местоположения линейного объекта в пространстве. Чем сложнее линия, тем больше точек нам потребуется для указания точного ее расположения. Если мы возьмем в качестве примера линейного объекта реку, то описание многих ее поворотов и излучин потребует большого числа точек, поскольку может быть желательным изображать больше, чем только начальную и конечную точки реки. Опираясь не геометрию, мы можем также определять формы и ориентации линейных объектов, чем займемся позднее.

Объекты, рассматриваемые с достаточно близкого расстояния, чтобы иметь и длину и ширину, называются областями или площадными объектами. Примеры областей, или "двухмерных" объектов, включают территории, занимаемые двором, городом или целым континентом. При определении местоположения области в пространстве мы обнаруживаем, что ее граница является линией, которая начинается и кончается в одной и той же точке. Помимо указания местоположения областей через использование линий, мы можем себе представить теперь три характеристики: как и для линий, мы можем указывать их форму и ориентацию, а теперь еще и величину площади, которую область занимает.

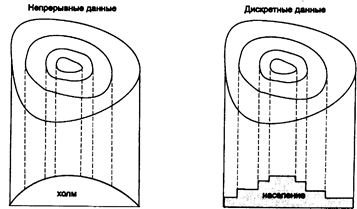
Рисунок 2.3. Непрерывные и дискретные поверхности. Заметьте, что изображение поверхности с помощью изолиний не проявляет ее дискретный или непрерывный характер.

Добавление нового измерения, высоты, к площадным объектам позволяет нам наблюдать и фиксировать поверхности. Хотя мы можем рассматривать дом с близкого расстояния и описывать его в терминах его общей длины и ширины, нам часто нужно знать, сколько в нем этажей. В таком случае нам нужно рассматривать дом не как плоскую область, а как трехмерный объект, имеющий длину, ширину и высоту. Поверхности окружают нас повсюду Холмы, долины, гряды гор, скалы и множество других образований могут описываться указанием их местоположения, занимаемой площади, ориентации, и теперь, с добавлением третьего измерения, их высот. Оказывается, что поверхности состоят из бесконечного числа точек со значениями высот. Мы говорим, что онинепрерывны (continuous), поскольку эти точки распределены без разрывов, непрерывно, по всей поверхности (Рисунок 2.3). В действительности, поскольку высота трехмерного объекта меняется от точки к точке, мы можем также измерять величину изменения высоты с перемещением от одного края до другого. Имея такую информацию, мы можем определить объем материала в выбранном образовании. Возможность таких вычислений весьма полезна, когда нам нужно узнать, сколько воды содержится в водоёме или сколько материала (пустой породы) лежит поверх угольного пласта.

Все эти феномены, будь то точечные, линейные, площадные или поверхностные, существуют в пространстве. И всем им может быть приписано определенное местоположение, где их можно найти. Но как мы можем выразить важность кругового площадного объекта, расположенного в определенной области, занимающего 10 гектаров и ориентированного с севера на юг? Нам нужен способ классификации таких объектов, основанный на других наблюдаемых их свойствах и использующий терминологию, которую могут понимать другие люди.

ШКАЛЫ ИЗМЕРЕНИЙ

До сих пор мы рассматривали лишь геометрические объекты, с которыми, как мы видели, ассоциированы наборы координат, позволяющие указать их расположение в пространстве. Картографические объекты содержат информацию не только о том, как они занимают пространство, но и о том, чем они являются и насколько они важны для нашего рассмотрения. Например, дерево, обозначенное как точечный объект, может быть отнесено к определенному классу на основе таксономической терминологии, то есть дуб, сосна и т.п. Мы можем узнать также возраст дерева, пробурив его и подсчитав годовые кольца. С этой дополнительной информацией мы теперь знаем, что есть не просто некоторое дерево, расположенное в некоторой точке пространства, но что это, скажем, дуб тридцати пяти лет. Дополнительная непространственная информация, помогающая нам описывать объекты, наблюдаемые в пространстве, образует наборатрибутов объектов. Когда мы наблюдаем наше пространственное окружение, мы начинаем распределять его атрибуты по категориям и отмечать где они находятся. В нашей природе, природе существ любознательных, заложено желание классифицировать, давать ярлыки вещам, которые нам попадаются, для того, чтобы мы могли привнести дополнительный уровень организации в наше пространство. И теперь мы можем указать, что определенный объект с определенным названием и с некоторыми измеримыми атрибутами существует в определенном месте.

Но перед тем как присвоить эти атрибуты объектам, мы должны знать, как их измерять. Иначе мы не сможем сравнивать объекты в одном месте с объектами в другом месте. Каким эталоном нам пользоваться? Насколько точно мы можем описывать объекты, с которыми имеем дело? Какой эффект будут иметь различные уровни точности измерений на нашу способность сравнивать объекты?

К счастью, уже существует устоявшаяся основа для измерения практически всех видов данных, в том числе и географических. Эти так называемыешкалы измерения данных (levels of data measurement) простираются от простого именования объектов, для того, чтобы мы могли называть их, до высокоточных измерений, позволяющих нам непосредственно сравнивать качества различных объектов. Используемая шкала измерений будет определяться отчасти тем, что мы классифицируем, отчасти тем, что мы хотим знать, и отчасти нашими возможностями производить измерения при заданном масштабе наблюдения. Рисунок 2.4 иллюстрирует шкалы измерений в связи с тремя обычно используемыми типами географических объектов.

На первом уровне находитсяноминальная шкала (nominal scale), из названия которой следует, что объекты различаются по именам. Эта система позволяет нам делать высказывания о том, как называется объект, но не позволяет делать прямого сравнения одного объекта и другого, за исключением определения тождества. Например, мы можем сказать, что в одном месте находится клён, а в другом - дуб. Хотя такое утверждение, несомненно, различает эти объекты, мы не можем их сравнивать, поскольку они различны по природе. То есть, мы не можем утверждать, что церковь лучше или хуже, чем пожарная станция, так же как мы не можем делать подобных утверждений относительно яблок и апельсинов.

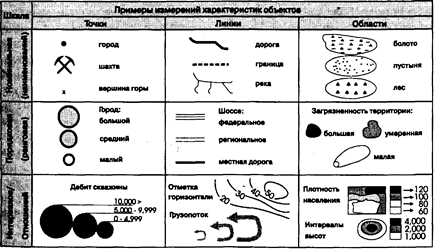
Рисунок 2.4. Шкалы измерения картографических объектов.

Если мы хотим провести более тонкое сравнение объектов, нам следует выбрать более высокую шкалу измерений. В нашем примере с деревьями, если бы мы захотели выяснить, насколько хороши клён, ясень или сосна в качестве декорации для пикника, мы могли бы поместить их напорядковую шкалу (ordinal scale), от лучшего к худшему для данного конкретного вопроса. Поскольку сосны часто имеют низкие ветви и сбрасывают кусочки коры и смолы на землю, мы, вероятно, отнесли бы их к наихудшему случаю среди этих трех. Хотя ясени производят меньше мусора и не имеют низких ветвей, их листья малы, и некоторое количество солнечных лучей проникнет через крону. Мы можем отнести ясень к среднему варианту для пикника. В противоположность ясеню, клён создаёт очень густую тень, к тому же он не производит много мусора и не имеет низких ветвей. Следовательно, мы можем отнести его к наилучшему классу на нашей порядковой шкале.

В нашем примере с пикником мы создали спектр значений от лучшего к худшему. Очевидно, однако, что этот спектр основан исключительно на цели использования данной информации и не может относиться к другим применениям деревьев. К примеру, ни клён, ни ясень не интересны для Рождества. Таким образом, наша классификация основана на одном аспекте, отражающем один набор условий. Далее: очевидно, что порядковые данные могут дать нам некоторое представление о последовательном сравнении пространственных объектов, но эти сравнения ограничены данным частным применением. Возьмем другой пример: отметку, которую вы получите за курс геоинформатики, нельзя сравнить с отметкой, полученной за дифференциальное исчисление. Здесь действуют два принципиально различных набора критериев. Если мы хотим быть более точными в наших измерениях, нам нужно воспользоватьсяинтервальной шкалой (interval scale) измерения, в которой измеряемым величинам приписываются численные значения. Как и в случае порядковой шкалы, здесь мы тоже можем сравнивать объекты, но здесь эти сравнения могут делаться с более точной оценкой различий. Хорошим примером пространственных данных, измеряемых в интервальной шкале, является температура почвы на некоторой исследуемой площади с существенно различными типами почв. Мы можем обнаружить, что температура очень темной, богатой перегноем почвы значительно выше температуры более светлой почвы с низким содержанием органического материала. В частности, мы можем сказать, что в одно время температурная разница между разными видами почв составляет 4°С, более темная почва имеет температуру 29^оС, в то время как более светлая - только 25^оС. Теперь мы имеем легко измеримую, точно градуированную разницу между почвами в двух выбранных местах.

Но остается одно ограничение при выполнении сравнений в интервальной шкале. Возьмем еще два, предельно различных вида почв, один - практически белый, а другой - почти черный. При измерении их температуры в одно время мы можем получить числа 10°С и 20°С. Как и раньше, мы можем получить численную разность между этими величинами 10°С. Но можем ли мы при этом сказать, что темная почва вдвое теплее светлой? На первый взгляд так и есть. Но нам следует вспомнить, что начало шкалы Цельсия выбрано произвольно. А для того, чтобы вычислить отношение двух величин, нужно иметь шкалу, на которой 0 представляет действительное начало температур. В данном примере нам следует перевести все величины в шкалу Кельвина, в которой начальная точка соответствует полному отсутствию движения молекул, с которым связано тепло. И когда мы преобразуем наши величины в соответственно 283 К и 293 К, мы увидим, что темная почва вовсе не вдвое теплее светлой.

В результате перехода от шкалы Цельсия к шкале Кельвина мы оказались на последней и наиболее "количественной" шкале измерений - шкале отношений (ratio scale). Преобразовав температуры в абсолютную шкалу, мы смогли получить осмысленное отношение величин, поскольку мы действовали теперь на шкале отношений*.

Может быть полезен и другой пример, поскольку он использует параметры, которые нам часто интересны. Допустим, мы исследуем две группы домов, расположенных в разных частях города: одна - в богатом районе пригорода, другая — в районе жителей с невысоким доходом, внутри города. Обследовав жителей, мы получили среднегодовой доход в первом районе 50000 долларов, во втором — 25000. Поскольку 0 долларов означает отсутствие дохода вообще, мы можем спокойно утверждать, что имеем дело со шкалой отношений и, следовательно, можем вычислять относительное различие. Разделив одну величину на другую, мы можем корректно утверждать, что среднегодовой доход семьи в первом районе вдвое больше, чем во втором. Однако, как и в случае негеографических данных, они корректны только с данными шкалы отношений.