Равновесие в гетерогенных системах. Правило фаз.

Принцип Ле Шателье применим не только к гомогенным, но и к гетерогенным системам. В качестве примера рассмотрим гетеро­генную химическую реакцию восстановления оксида углерода (IV)

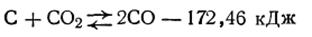
Эта система содержит твердую фазу (уголь) и газообразную (смесь паров СО₂ и СО). Поскольку процесс восстановления СО₂ идет с поглощением тепла, т.е. является эндотермическим, то согласно принципу Ле Шателье нагревание системы сместит равновесие в сторону увеличения выхода СО, а ее охлаждение будет сдвигать равновесие влево. Изменение давления также окажет существенное влияние на ход этой реакции, так как она в направлении слева направо сопровождается увеличением числа молей газообраз­ной фазы. Повышение давления будет препятствовать протеканию прямого процесса, а уменьшение давления — способствовать ему.

Опыт показывает, что если гетерогенная реакция протекает без изменения числа молей газообразной фазы, то изменение общего давления не оказывает влияния на состояние равновесия реакции. В качестве примера можно указать такие реакции:

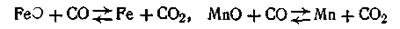
Закон действующих масс применим к гетерогенным системам лишь с определенными допущениями. Область его приложения ограниче­на однородными частями равновесной системы. Равновесие же между неоднородными частями системы не подчиняется закону дей­ствующих масс.

Рассмотрим в качестве примера гетерогенную реакцию диссо­циации карбоната кальция при высокой температуре в замкнутом сосуде: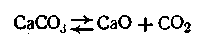

В этой системе СаСО₃ и СаО находятся в твердом состоянии, а СО₂ — в газообразном. Если бы вышеуказанная реакция протека­ла как гомогенная реакция в газовой фазе (что можно допустить), можно было бы написать

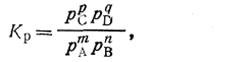
2.42

где 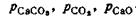— упругости паров соответственно СаСО₂, СО₂ и СаО.

Однако упругости паров твердых СаСО₃ и СаО являются для данной температуры величинами постоянными, поэтому

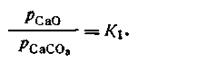
2.43

Подставив это выражение в уравнение (2.42), получим:

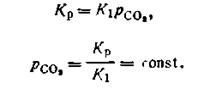
2.44

Равенство (2.44) показывает, что давление рсо₂может иметь только одно определенное значение при данной температуре. Это давление называется давлением диссоциации СаСО₃ или упруго­стью диссоциации. Оно не зависит от концентрации СаСО₃ и СаО в данной системе.

Опыт показывает, что давление диссоциации для реакции 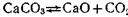достигает 0,1 МПа при температуре 1153 К, в то время как при 773 К это давление составляет всего лишь 14,67 Па. Следовательно, при температуре 1153 К начинается ин­тенсивное разложение СаСО₃.

Качественная характеристика гетерогенных равновесных систем, в которых не происходит химического взаимодействия, а наблюда­ется лишь переход составных частей системы из одного агрегатного состояния в другое, дается правилом Гиббса. Это правило основа­но на втором законе термодинамики и относится к системам, нахо­дящимся в состоянии истинного равновесия.

Введем основные понятия : фаза, компонента и степени сво­боды.

Фаза — совокупность частей гетерогенной системы, обладающих одинаковым составом и свойствами и отделенных от других состав­ных частей ограничивающими поверхностями. При переходе через поверхности происходит скачкообразное изменение свойств ве­ществ, образующих данную гетерогенную систему. Фаза может быть простой и смешанной.

Простая фаза состоит из одного химически индивидуального ве­щества (например, бензол в виде эмульсии в воде образует чистую фазу).

Смешанная фаза состоит из двух или более химически индиви­дуальных веществ (например, смеси газов, жидкие и твердые рас­творы).

Любая фаза может представлять собой сплошную массу (напри­мер, вода в суспензии глины в воде) или же совокупность более или менее крупных частиц (капельки воды, образующие туман в воз­духе, составляют одну фазу).

Вещества, которые входят в состав системы и которые могут быть извлечены из системы и существовать вне ее, называются со­ставляющими веществами.

Например, водный раствор сахара об­разован из двух составляющих: воды и сахара.

В химических системах некоторые составляющие вещества мо­гут образоваться в результате химического процесса, протекающе­го в системе. Такие составляющие вещества называются зависимы­ми. Первоначально же взятые составляющие систему вещества на­зываются независимыми.

Компонентами называются независимые составляющие, наи­меньшего числа которых вполне достаточно, чтобы построить любую фазу в системе, находящейся в равновесии. В физических системах число компонентов равно числу составляющих систему веществ, так как последние не вступают между собой в химическое взаимо­действие. В химических же системах число компонентов меньше числа составляющих веществ на число химических уравнений, по которым вещества, образующие систему, обратимо реагируют меж­ду собой при данных условиях существования системы.

Рассмотрим подсчет числа компонентов на конкретных приме­рах. Возьмем равновесную гетерогенную систему

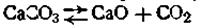
Система химическая, составляющих веществ три. Число уравне­ний химических реакций в системе равно одному. Число компонентов в системе равно 3—1=2. Значит, система эта двухкомпонентная.

Другой пример. Рассмотрим систему из трех веществ, в которой между составляющими протекает реакция

т. е. реакция разложения NH₄Cl. Оба продукта реакции — NH₃ и НСl — находятся в газообразной фазе, и равенство числа образо­вавшихся молей приводит к уравнению равенства концентраций (в кмоль/м³)

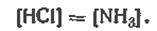
В этом случае мы имеем дело с двумя уравнениями, которыми свя­заны составляющие вещества:

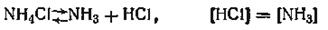
Таким образом, число компонентов в этой системе будет равно 3—2=1, где 3 — число составляющих веществ, 2 —число уравне­ний, их связывающих. Как видим, данная система будет однокомпонентной.

Число степеней свободы характеризует вариантность системы, т. е. число независимых переменных (давление, температура и концентрация компонентов), которые можно произвольно изменять в некоторых пределах так, что число равновесных фаз в системе остается неизменным.

Например, состояние идеального газа характеризуется тремя параметрами: р, V, Т. Из них любая пара является независимыми переменными, характеризующими термодинамическое состояние системы, которое можно изменить произвольно, без нарушения ви­да и числа фаз в системе. Иными словами, число степеней свободы для идеального газа равно двум, что соответствует двум произволь­но заданным параметрам: р и Т; р и С или С и Т, а третий будет определен из уравнения состояния.

Другой пример. Равновесная система лед↔вода↔пар сущест­вует при строго определенных параметрах: T=273,16 К и р = 610,48 Па. Эта система состоит из трех фаз и одного компонен­та (вода). Незначительное изменение хотя бы одного из парамет­ров приводит к смещению равновесия в сторону изменения числа фаз системы. Так, повышение температуры будет способствовать переходу воды в пар, в результате чего число фаз уменьшится. К аналогичному нарушению равновесия системы приведет и из­менение давления. Таким образом, для рассматриваемой системы степень свободы равна нулю, т. е. нет таких параметров, изменение которых не нарушило бы термодинамического равновесия данной системы.

Гиббс (1878) вывел следующее уравнение, выражающее усло­вия фазового равновесия:

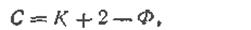
2.45

где С — число степеней свободы; К — число компонентов; Ф — чис­ло фаз в системе.

Это соотношение известно как закон равновесия фаз и называ­ется правилом фаз. Правило фаз имеет следующую формули­ровку: в равновесной многофазной системе число степеней свободы равно числу компонентов плюс два, минус число фаз.

Из уравнения (2.45) можно сделать сле­дующие выводы:

1) чем больше компонентов содержит система (при данном числе фаз), тем больше степень ее свободы;

2) чем большее число фаз находится в равновесии между со­бой в системе (при данном числе компонентов), тем меньшее чис­ло степеней свободы имеет система.

Лишенную степеней свободы систему (например, лед — вода — пар) предложено называть инвариантной. Если число степеней свободы С=1, такую систему называют моновариантной, если С=2, то бивариантной, и т. д.

В настоящее время правило фаз является критерием равновес­ного состояния систем и помогает в решении ряда производствен­ных задач, связанных с процессами в химических многофазных си­стемах. Это правило широко применяется в различных областях химии и химической технологии, особенно в металлургии, в производстве различных стройматериалов, пласт­масс.

Большой вклад в развитие учения о фазовых превращениях был внесен советскими учеными Н. С. Курнаковым, А. И. Цветко­вым и др.