Максимальной работой реакции.
Химическая система в состоянии равновесия отвечает наименьшему запасу свободной энергии. Любое отклонение от равновесного состояния сопровождается возрастанием свободной энергии в системе. В этом случае, согласно второму началу термодинамики, возникает процесс самопроизвольного перехода данной системы в сторону уменьшения свободной энергии, за счет выделения которой возможно совершение полезной работы.
Максимальная работа изотермической реакции при постоянном давлении и постоянной температуре определяется изменением так называемого изобарного потенциала ∆G. Эта величина характеризует максимальную полезную работу реакции и указывает на направление протекания реакции.
Максимальная работа реакции связана с константой равновесия простым соотношением, которое впервые было выведено Вант-Гоффом в 1885 г. Он доказал, что между константой химического равновесия и разностью приращения свободных энергий существует логарифмическая зависимость ∆Wмакс= -∆G = RTlnK,где R— универсальная газовая постоянная, Т — термодинамическая температура по Кельвину.
В том случае, когда парциальные давления или концентрации принимавших участие в реакции веществ равны единице, вторые члены правых частей этих уравнений обращаются в нуль и они принимают вид
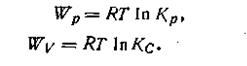
| 2.54 |
Следует отметить, что по смыслу максимальная работа при постоянном давлении равнозначна изменению изобарно-изотермического потенциала, взятому с обратным знаком, т. е. Wp = —∆G. По аналогии с этим максимальная работа при постоянном объеме равна изменению изохорно-изотермического потенциала, взятому также собратным знаком, т. е. WV = —∆A.
Для стандартных условий (T = 298 К, Р = 0,101325 МПа)
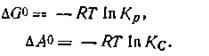
| 2.55 |
Мерой химического сродства реагирующих веществ служит максимальная работа в условиях, когда концентрация или парциальные давления реагирующих веществ равны единице.
Если реакция еще протекает и не достигла равновесия, то изменение изобарного потенциала равно:
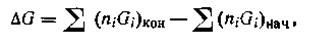
| 2.56 |
т. е. изменение изобарного потенциала ∆G (или, что то же самое, изменение свободной энергии), отвечающее протеканию какой-нибудь данной химической реакции, равно разности между изобарными потенциалами конечных продуктов реакции и исходных веществ. Так, для химической реакции типа mA + nB = pC+qD имеем:
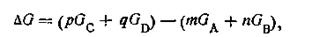
| 2.57 |
где GС, GD, Ga и Gb — изобарные потенциалы компонентов. Поскольку значения этих потенциалов неизвестны, вместо них используют значения изменений изобарного потенциала, происходящих при образовании данного соединения из простых веществ, при стандартных условиях (при Т = 298 К и при постоянном давлении Р= 101,325 кПа), называемого в термодинамике потенциалом образования и обозначаемого символом ∆G°298.
В частности, для реакции, приведенной выше, можем написать
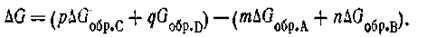
| 2.58 |
Если ∆G реакции имеет отрицательное значение, то реакция идет свыделением энергии. В этом случае она протекает самопроизвольно в данном направлении.
Рассмотрим в качестве примера реакцию получения кристаллического сульфата алюминия из Аl2О3 и газообразной трёхокиси серы при 298 К (все в стандартных состояниях):
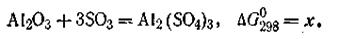
Пользуясь табличными данными, получим:
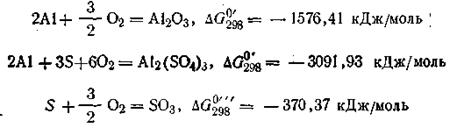
Для определения ∆G°298 реакции воспользуемся уравнением (2.58):
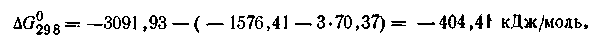
Данная реакция идет самопроизвольно, так как ∆G°298 этой реакции имеет отрицательное значение. Таким образом, зная ∆G°298 длявсех веществ, участвующих в реакции, можно рассчитать ∆G0298 и самой реакции, а следовательно, и направление этой реакции.
Вопросы для самоподготовки
1. Предмет химической кинетики. Скорость химической реакции и факторы, ее определяющие.
2. Классификация химических реакций по молекулярности и порядку. Дайте понятие о константе скорости и периоде полураспада реакции. Запишите кинетические уравнения первого и второго порядков.
3. Охарактеризуйте основные методы определения порядка реакции.
4. Укажите законы, характеризующие влияние температуры на скорость реакции.
5.Активированный комплекс, энергия активации и способы ее определения.
6. Понятие о катализе, его виды и сущность основных теорий катализа.
7. Ферментативный катализ. Факторы, влияющие на активность ферментов. Чем определяется химическая и специфическая активность ферментов.
ЗАДАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ 2
ЗАДАНИЕ 1. Определение константы скорости реакции инверсии сахарозы.
Цель работы:
1. Освоить методику изучения кинетики химических процессов.
2. Определить константу скорости реакции инверсии сахарозы поляриметрическим методом (см. с. 134-137 ).
3. Определить порядок реакции инверсии сахарозы.
ЗАДАНИЕ 2. Изучение влияния концентрации катализатора на скорость инверсии сахарозы.
Цель работы:
1. Освоить методику исследования кинетики химических процессов.
2. Определить константу скорости инверсии сахарозы поляриметрическим методом при разных концентрациях катализатора (см. с. 134-137).
3. Сделать выводы о влиянии концентрации катализатора на скорость реакции.
ЗАДАНИЕ 3. Изучение влияния температуры на скорость химических реакций.
Цель работы:
1. Освоить методику исследования кинетики химических процессов.
2. Определить константу скорости инверсии сахарозы поляриметрическим методом при разных температурах (см. с. 134-138).
3. Сделать выводы о влиянии температуры на скорость химических реакций.
4. Рассчитать температурный коэффициент и энергию активации системы.
ЗАДАНИЕ 4. Исследование кинетики биохимических процессов.
Цель работы:
1. Освоить методику изучения кинетики биохимических процессов.
2. Исследовать кинетику процесса превращения сахаров во фруктовых соках в присутствии фермента при различных значения рН (см. с. 138).
3. Сделать вывод о влиянии рН на активность фермента.
ЗАДАНИЕ 5. Изучение кинетики реакции фуксинсернистой кислоты с формальдегидом.
Цель работы:
1. Освоить методику изучения кинетики различных процессов.
2.Определить константу скорости реакции относительно фуксинсернистой кислоты при различных ее концентрациях (см. с. 138-140 ).
3. Сделать выводы о порядке реакции.
ЗАДАНИЕ 6. . Изучение кинетики реакции образования железороданидного комплекса.
Цель работы:
1. Освоить методику изучения кинетики различных процессов.
2.Определить константу скорости реакции относительно железороданидного комплекса при различных концентрациях сульфата железа (см. с. 138-141).
3. Сделать выводы о порядке реакции.
ЗАДАНИЕ 7. Определение константы скорости реакции взаимодействия трихлорида железа с иодидом калия.
Цель работы:
1. Освоить методику изучения кинетики химических процессов.
2. Определить константу скорости реакции взаимодействия хлорида железа (Ш) с иодидом калия( см. с.141 -142).
3. Определить порядок реакции.
ИЗУЧЕНИЕ КИНЕТИКИ РЕАКЦИИ ИНВЕРСИИ САХАРОЗЫ
Сахароза присутствует во всех фотосинтезирующих растениях, перемещается из листьев в семена, корни, клубни и луковицы, где легко превращается в крахмал или инулин. Углеводы легко гидролизуются под действием фермента инвертазы или кислот на глюкозу и фруктозу по схеме
С12Н22О11 + Н2О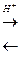 
С6Н12О6 + С6Н12О6
Это – процесс инверсии, сопровождающийся изменением угла вращения плоскости поляризованного света. При этом изменение угла вращения прямо пропорционально содержанию сахарозы в растворе, что позволяет определить скорость этого процесса с помощью поляриметра (см. инструкцию работы с прибором).
Скорость реакции инверсии сахарозы зависит лишь от изменения концентрации сахарозы, поскольку вода присутствует в очень большом избытке и ее количество в течение реакции практически не меняется. Такие реакции могут быть описаны кинетическим уравнением реакции первого порядка (см. уравнение 2.10 ).
Для процесса инверсии:
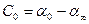
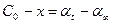
где: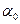 
- угол поляризации в начале опыта;
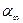- угол поляризации в равновесном растворе;
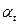- угол поляризации для данного момента времени.
При подстановке этих значений в уравнение (2.10) получается рабочее уравнение для вычисления константы скорости реакции инверсии сахарозы:
К1 =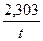 
lg 
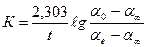. (2.59)
МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ
Изучение кинетики реакции состоит из нескольких этапов:
1.В чистую сухую колбу из бюретки отмеряют 10 см3 раствора HCI заданной концентрации (1 н или 1,5 н) и 10 см3 раствора сахарозы. Кислота является катализатором. Растворы сливают, перемешивают и заливают в поляриметрическую трубку. Убедившись в отсутствии пузырьков воздуха, трубку помещают в поляриметр и измеряют угол вращения плоскости поляризации для начального момента времени ( 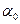). Отсчет берут в 3-х кратной повторности и находят среднее значение .
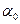2. Не вынимая трубки из поляриметра, измеряют углы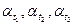 
и т.д., через заданные интервалы времени.
3. Для измерения угла вращения в равновесном растворе ( 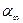) необходимо воспользоваться заранее приготовленной смесью или оставить реагирующую смесь на 24 часа и также произвести измерения a¥.
Результаты измерения заносят в табл. 2.2, оформленную согласно заданию.
ЗАДАНИЕ 1.Целью этого задания является установление порядка реакции.
Физический смысл установления порядка реакции заключается в определении числа молекул веществ, от изменения концентрации которых зависит скорость реакции, что позволяет установить механизм химического взаимодействия в рассматриваемой системе.
Одним из методов определения порядка реакции является метод подстановки в кинетические уравнения реакции. Сущность его заключается в том, что производят расчет величины константы скорости изучаемой реакции, используя экспериментальные измерения путем их подстановки в кинетическое уравнение реакции первого порядка, и по постоянству значений константы скорости устанавливают порядок реакции. Если, например, подстановка экспериментальных данных в кинетическое уравнение первого порядка и расчет показали постоянство величины константы скорости, то эта реакция первого порядка. Результаты поляриметрических измерений заносят в табл. 2.2
По полученным данным, пользуясь уравнением (2.59), вычисляют значение константы скорости для разных промежутков времени, затем определяют ее среднее значение К (ср.) –см. уравние (2.60).
Таблица 2.2 Результаты поляриметрических измерений
| Измерение | Время реакции, мин. | Угол вращения плоскости поляризации | К | |||
| 1-е измерение | 2-е измерение | 3-е измерение | Среднее | |||
| … | … | |||||
| N |
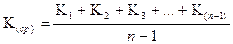, (2.60)
Рассчитывают среднюю ошибку работы:
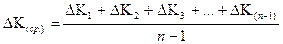, (2.61)
где: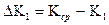 
, 
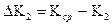и т.д. ( 2.62)
Если средняя ошибка незначительна, в пределах до 5×10-3, то это означает, что значения константы скорости для разных промежутков времени близки друг к другу. Следовательно, изученная реакция подчиняется закономерностям кинетического уравнения первого порядка и является реакцией первого порядка.
ЗАДАНИЕ 2. Предполагает изучение влияния концентрации катализатора (хлористоводородной кислоты) на скорость процесса гидролиза сахарозы. Растворы готовятся и измеряются углы вращения согласно методике, описанной выше (см. с 13 ) с двумя концентрациями кислоты: 1н и 1,5 н. Данные опыта заносятся в две таблицы (см. табл. 2) с указанием концентрации катализатора.
По уравнению (2.59) рассчитывают Кv и находят средние значения констант скорости ( ур-ние 2.61 ) при 1,0 н и 1,5 н концентрациях хлористоводородной кислоты. Значения полученных К сравнивают и делают выводы о влиянии концентрации катализатора на скорость реакции.
ЗАДАНИЕ 3. Зависимость скорости реакции от температуры выражается правилом Вант-Гоффа, то есть температурный коэффициент реакции равный отношению констант К(Т+10) и КТ будет от 2 до 4
g =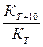 
= 2 - 4(2.63)
Для установления влияния температуры на скорость процесса гидролиза сахарозы, а также расчета значения температурного коэффициента, необходимо провести процесс – при двух различных температурах, например, один при температуре окружающей среды (Т), а другой – на 10 0С выше -(Т+10). Методику приготовления раствора см. с. 111 . Данные заносят в табл. 2.2 и по уравнению (2.59) рассчитывают скорости для различных температур, а затем, используя закон Вант-Гоффа - уравнение (2.63), находят значение температурного коэффициента и делают выводы. Для расчета энергии активации системы используют математический способ, в основе которого лежит решение системы уравнений Аррениуса :
ln KT = ln K0 - 
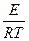
ln KT+10 = ln K0 -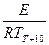 
Откуда
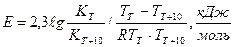(2.64).
ЗАДАНИЕ 4. К 50 см3 фруктового или овощного сока (виноградного, яблочного, морковного или других) приливают 10 см3 10%-го раствора уксуснокислого свинца (для осаждения растворимых фракций). Раствор фильтруют, фильтр промывают 10 см3 дистиллированной воды и соединяют с основным фильтратом. Для выделения избытка ионов свинца к фильтрату прибавляют 10 см3 10%-го Na2SO4.
Раствор повторно фильтруют в мерную колбу объемом 100 см3, промывают фильтр дистиллированной водой (не более 5 см3) и доводят объем раствора в колбе до метки водой. Далее опыт проводят согласно вышеописанной методике (см. стр. 110-113 ).
Приготовленные испытуемые растворы разливают в две колбы: в одну колбу добавляют 10 см3 1н HCl, в другую столько же – 1,5н HCl. Для измерения a¥ готовую смесь оставляют до следующего занятия. Данные заносят в таблицу. Расчет константы скорости проводят по уравнению (2.59) и делают выводы.
ЗАДАНИЕ 5,6. Изучение кинетики реакции функсинсернистой кислоты с формальдегидом и реакции образования железороданидного комплекса.
При взаимодействии функсинсернистой кислоты с формальдегидом и реакции образования железороданидного комплекса наблюдается изменение окраски раствора, поэтому измерение концентрации в ходе реакции можно проводить фотоколориметрическим методом с помощью КФК-2 при 490нм ( для реакции фуксинсернистой кислоты с формальдегидом) и при 400 нм ( для железороданидного комплекса) (см. инструкцию измерения на приборе). Относительно трифенилметанового и железороданидного комлексов реакция 1 порядка, а, следовательно, её ход описывается кинетическим уравнением:
К1 = 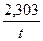lg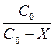 
,
где Со –Х = С и так как при t = 0, С0 = 0 идет изменение концентрации окрашенного комплекса, то: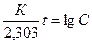 
.
Так как определение концентрации через определенные интервалы времени проводится по изменению абсорбции света (Dλ), то
C=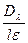 
и lgJO/J= 
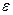Cl=Dl (2.65)
где: 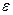и l- величины постоянные для данного процесса, следовательно, построив графическую зависимость (см. рис. 2.7), описывающую уравнение (2.65), можно найти:
lg Dl K = 2,303 tg a (2.66)
1
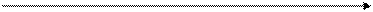
2
t, время
Рис. 2.7. Примерный график зависимости абсорбции света (Dλ)
от времени течения реакции (t).
МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ
Для определения порядка реакции используют метод избытка:
для выполнения работы 5 в чистую колбу отмеряют 10 см3 0,1%-го раствора формальдегида и вносят туда же с помощью пипетки 0,2см3 1 %-го раствора функсинсернистой кислоты. Раствор взбалтывают, быстро наливают в кювету и измеряют абсорбцию света через каждую минуту. Данные заносят в табл. 2.3. Измерения прекращают, если 3-4 значения Dλ одинаковы. Опыт повторяют. Берут 20 см3 0,1%-го формальдегида и 0,4 см3 1%-го раствора функсинсернистой кислоты, занося данные в табл. 2.3 (измерение 2).
Строят графические зависимости, откладывая на оси абсцисс t (мин.), а по оси ординат - lg Dλ (рис. 2.7). Измерив угол наклона прямой (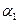 
и 
) и 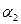найдя численное значение - 
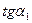и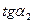 
, вычисляют К1 и К2 по уравнению (2.66). Если К1 и К2 имеют близкие значения, то данная реакция относится к реакциям 1 порядка относительно фуксинсернистой кислоты
Таблица 2.3 Результаты измерений абсорбции света
| Время, t, мин. | Измерение Dλ | |
| … | ||
для выполнения работы 6наливают в мерную колбу объемом 100 см3 40 см3 раствора Fe2 (SO4 )3 c концентрацией 1∙ 10-5 г/см3 .К отобранному раствору приливают 1см3 HNO3 ( 1: 1) и 5 см3 10 % раствора NH4 CNS, доливают до метки водой и тщательно перемешивают и сразу измеряют абсорбцию света. Проводят 5-6 измерений через каждые 10 мин. Данные заносят в таблицу 2.4 (столбец 1).
Таблица 2.4 Результаты измерений абсорбции света
| Время, t, мин. | Измерение Dλ | |
| … | ||
Опыт повторяют. Берут 25 см3 см3 раствора Fe2 (SO4 )3 c концентрацией 1∙10-5 г/см3 .К отобранному раствору приливают 1см3 HNO3 ( 1: 1) и 5 см3 10 % раствора NH4 CNS, доливают до метки водой, тщательно перемешивают и сразу измеряют абсорбцию света. И опять проводят 5-6 измерений через каждые 10 мин. Данные заносят в таблицу 2.4 ( столбец 2 ).
Строят графические зависимости, откладывая на оси абсцисс t (мин.), а по оси ординат - lg Dλ (рис. 2.7). Измерив угол наклона прямой ( 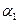и ) и 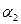найдя численное значение - 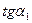и 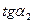, вычисляют К1 и К2 по уравнению (2.67). Если К1 и К2 имеют близкие значен
ия, то данная реакция относится к реакциям 1 порядка.
ЗАДАНИЕ 7. Определение константы скорости реакции
взаимодействия трихлорида железа с иодидом калия.
Реакция взаимодействия трихлорида железа с иодидом калия характеризуется уравнением
FeCl3+ 2KJ® 2FeCl2 + 2KCl + J2,
из которого следует, что образование J2 изменяет окраску раствора, и, следовательно, за ходом этой реакции можно наблюдать фотоколориметрическим методом с помощью КФК-2, 3 при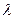 
= 400 нм.
Реакция является бимолекулярной, а значит, ее скорость зависит от концентрации обоих реагентов:
V = K [FeCl3] [KJ].
Поскольку эксперимент проводят при равных концентрациях исходных [FeCl3] = [KJ] , то в общем виде можно записать:
V = KC2, следовательно, кинетическое уравнение реакции П порядка имеет вид:
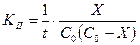, (2.68)
где: С0 - начальная концентрация реагентов, моль/дм3;
Х - уменьшение концентрации реагентов за время t, моль/дм3.
МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ
1. Готовят фотокалориметр к работе (см. правила работы на приборе).
2. Готовят стандартный (эталонный) раствор: для этого смешивают в колбе 5 см 3 FeCl3 и 20 см 3дистиллированной воды .
3. В другую колбу отмеряют 5см3 FeCl3, 15см3 дистиллированной воды и 5 см3 KJ в указанной последовательности. Растворы тщательно перемешивают. В момент прилива KI начинают отсчет времени.
4. Заливают раствор в кювету и измеряют абсорбцию света (Dλ) при 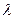= 400 нм через каждые 2 мин (от начала реакции). Измерения продолжают до получения 2-х одинаковых результатов Dλ. Данные заносят в табл. 2.5.
Таблица 2.5
| Время от начала реакции, t, мин | … |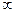 
| |||
| Оптическая плотность, Dλ | |||||
| Концентрация йода, С×103 моль/дм3 | |||||
| Константа скорости, [мин × моль/дм3] |
5. По данным, приведенным в табл. 2.6, строят калибровочный график Dl = f [J2] и по нему определяют концентрацию полученных растворов и ее значение заносят в табл.2.5.
Таблица 2.6 Данные для построения калибровочного графика
| Концентрация йода, С×103 моль/дм3 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 |
| Оптическая плотность Dl | 0.12 | 0.20 | 0.28 | 0.37 | 0.44 | 0.52 | 0.59 | 0.66 | 0.74 | 0.81 |
6. Рассчитывают значение константы скорости для каждого момента времени по концентрации J2, а, следовательно, уравнение будет иметь вид:
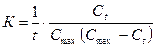, (2.69)
где Ct – концентрация йода для данного момента времени,
моль/дм3;
Cmax-концентрация в момент окончания реакции (соответствует
Dmax).
7. По полученным данным находят среднее значение
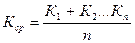
8. Рассчитывают среднюю ошибку работы по уравнению (2.61) и, если средняя ошибка незначительна, т.е. DКср< 5 10-3, то это означает, что константы скорости близки друг к другу, и изучаемая реакция является реакцией 2го порядка.
ТЕМА 3.
Дата добавления: 2016-02-20; просмотров: 1956;