Второе начало термодинамики. Понятие об энтропии.
На основе первого начала термодинамики невозможно установить, в каком направлении и до какого предела будет протекать тот или иной процесс, связанный с превращением энергии. Второе начало термодинамики определяет направление превращения энергии, т. е. указывает, какой процесс и в каком направлении может протекать при данных условиях температуры, давления и концентрации без сообщения энергии извне.
Из повседневных наблюдений над естественными процессами в природе известно, что многие из них проходят самопроизвольно без всяких внешних воздействий только в определенном направлении. Так, вода стекает по склону только вниз, а не наоборот, газ распространяется из области высокого давления в область низкого, теплота передается от более нагретого тела к менее нагретому. В обратном же направлении указанные процессы сами собой идти не могут и потому в этом случае они являются несамопроизвольными.
Отличительной чертой самопроизвольных процессов является их необратимость.
Опыт показывает, что всякий самопроизвольный процесс можно использовать для получения полезной работы. Например, падающая со склона или уступа вода может вращать мельничное колесо или турбину, расширяющийся газ — двигать поршень машины, химическую реакцию можно использовать как источник энергии. Несамопроизвольные переходы энергии могут происходить только при введении в систему энергии извне. Так, чтобы перекачать воду наверх, перенести теплоту из холодной системы в горячую (как в холодильной машине), сжать газ, необходимо затратить энергию. Поскольку во время протекания процесса всегда имеют место невосполнимые потери энергии в виде теплоты, работа, произведенная системой при самопроизвольном процессе, всегда меньше работы, затраченной на возвращение системы в исходное состояние.
Наряду с необратимыми процессами термодинамика рассматривает обратимые процессы, т. е. такие, которые могут идти как в прямом, так и в обратном направлениях при бесконечно малом изменении действующих на систему сил и без изменения работоспособности системы в обоих направлениях. В случае самопроизвольно происходящих изменений примерами таких идеальных обратимых процессов могут служить разрядка батареи через потенциометр, дающий разность потенциалов противоположного знака, и расширение газа в идеальном цилиндре с поршнем при медленном изменении противодействующего давления. Поскольку вполне равновесный процесс практически неосуществим, обратимый процесс есть процесс идеальный. Однако понятие обратимого процесса широко используется в термодинамике.
Во-первых, в случае обратимого (равновесного) процесса система совершала бы максимум полезной работы; поэтому, сравнивая величину работы, полученной в реальном процессе, с таковой в обратимом процессе, можно судить об эффективности процесса в прямом и обратном направлениях.
Во-вторых, реальный процесс (химическую реакцию) можно представить протекающим бесконечно медленно и обратимо, что позволяет наиболее просто и однозначно рассчитать термодинамические свойства системы.
Вопросы обратимости и необратимости различных физических и химических процессов, а также перехода теплоты в работу и работы в теплоту разрешаются вторым началом термодинамики. В этом и состоит его важное практическое значение. Зная направление перехода энергии, можно при наличии определенного механизма получить полезную работу.
Второе начало термодинамики имеет несколько равноценных формулировок, из которых наиболее часто используют следующие:
невозможен самопроизвольный переход энергии (в форме теплоты) от менее нагретого тела к более нагретому (постулат Клаузиуса, 1850);
невозможно создание вечного двигателя второго рода, т. е. машины, способной в течение принципиально неограниченного времени производить работу за счет отбора энергии (в форме теплоты) от некоторого источника без каких-либо других взаимодействий с окружающей средой (Томсон, 1851).
Исходя из этих формулировок, можно сделать вывод, что в замкнутой системе переход теплоты в работу будет совершаться только при наличии разности температур, т. е. при наличии нагревателя и холодильника, обусловливающих процесс перехода теплоты от тела более нагретого к более холодному. Причем при постоянной температуре теплота не может самопроизвольно превращаться в работу.
В связи с этим с точки зрения молекулярно-кинетических представлений второе начало термодинамики можно сформулировать следующим образом: все процессы, происходящие в природе, стремятся перейти самопроизвольно от состояния менее вероятного к состоянию более вероятному. Для молекул наиболее вероятным является беспорядочное, хаотичное движение, т. е. тепловое движение. Работа характеризуется более или менее упорядоченным движением частиц, каковое является менее вероятным. Отсюда самопроизвольный переход работы в теплоту можно рассматривать как переход молекулярной системы от упорядоченного движения частиц к более вероятному — хаотическому.
Рассмотрим работу тепловой машины, т. е. машины, производящей работу за счет теплоты, поглощаемой от какого-то тела — теплоотдатчика.
Ниже приведена схема работы такой машины.
Из схемы ясно, что не вся теплота Q1,получаемая рабочим телом, превращается в работу, а лишь некоторая ее часть W = Q1—Q2. Другая часть теплоты Q2 передается телу с более низкой температурой — теплоприемнику. Таким образом, сущность работы тепловой машины заключается не только в получении теплоты Q1 от теплоотдатчика и в совершении работы W, но и в передаче некоторого количества теплоты Q2 теплоприемнику, температура которого ниже, чем температура теплоотдатчика.
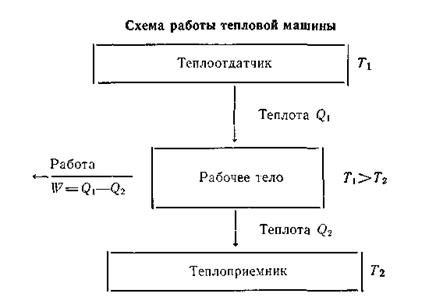
Следовательно, теплоту никогда не удается полностью (на сто процентов) превратить в работу. Там, где нет перепада температур, т. е. Т1 = Т2,невозможно превратить теплоту в работу. Если бы это условие не было необходимым, можно было бы использовать для получения полезной работы огромные природные запасы теплоты, заключенные, например, в водах морей и океанов. Однако необходимость иметь для этой цели теплоприемник с более низкой, чем вода в океане, температурой, естественно, сильно ограничивает и технически усложняет подобную возможность.
Допускаем, что масса теплоотдатчика так велика, что его температура в этом процессе заметно не изменяется. Поскольку внутренняя энергия идеального газа зависит только от температуры, то в данном процессе она остается постоянной, и потому работа расширения W1производится газом целиком за счет поглощения теплоты Q1:
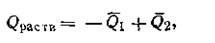
| 1.44 |
При небольших изменениях температуры теплоемкость газа практически остается величиной постоянной, поэтому изменение внутренней энергии идеального газа в этих условиях
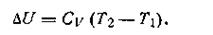
| 1.45 |
Работа, произведенная газом в этом процессе, в точности равна убыли внутренней энергии W2 = —∆U, откуда
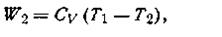
| 1.46 |
где Cv— теплоемкость газа при постоянном объеме.
Следовательно,
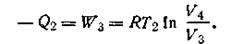
| 1.47 |
Общее количество теплоты, полученное газом, равно общему количеству произведенной им работы:
Подставив в это уравнение соответствующие значения W1 и W3, получим
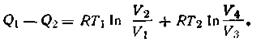
| 1.48 |
Используя уравнение адиабаты идеального газа, можно доказать, что
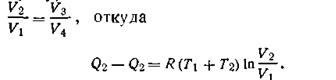
| 1.49 |
Или
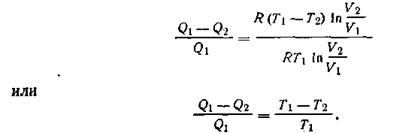
| 1.50 |
Коэффициентом полезного действия тепловой машины, η называется отношение количества полученной работы W к количеству поглощенной теплоты Q:
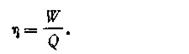
| 1.51 |
В рассмотренном случае W = Q1—Q2, где Q2— количество теплоты, отданное теплоприемнику, следовательно,
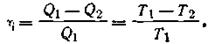
| 1.52 |
На основании этого соотношения второму началу термодинамики можно дать еще и такую формулировку: коэффициент полезного действия тепловой машины не зависит от природы и вида тел, участвующих в процессе, а зависит только лишь от разности температур теплообменника (Т1) и теплоприемника (Т2).
Так как Т1> Т2,то коэффициент полезного действия машин может изменяться в пределах от 0 (при Т1=T2) до 1 (когда T2 = 0К). Однако получить к. п. д. тепловой машины η = 1 невозможно, так как нельзя создать теплоприемник с температурой, равной абсолютному нулю. Поэтому даже в идеальном случае существует предел превращения теплоты в работу.
Все эти выводы получены, как уже подчеркивалось, для идеального газа в качестве рабочего тела. Следовательно, и невозможно построить такую машину, которая, получив Q джоулей теплоты, превратила бы в работу больше энергии, чем r\Q.
Общий вывод: любая форма энергии может полностью перейти в теплоту, но теплота преобразуется в другие формы энергии только частично.
Основываясь на этом, термодинамика доказывает, что внутренняя энергия U не может быть полностью превращена в работу при Т = const. Поэтому условно запас внутренней энергии системы можно представить в виде двух слагаемых:
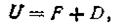
| 1.53 |
где F— полезная часть внутренней энергии, которая способна произвести работу и которая по предложению Гельмгольца названа свободной энергией; D — непроизводительная часть, так называемая связанная энергия, которая ни при каких условиях не может быть превращена в полезную работу и которая способна переходить только в теплоту и рассеиваться.
Свободная энергия в любой системе заключена в виде потенциальной энергии. По мере совершения системой работы ее энергия убывает. Чем больше система содержит свободной энергии, тем большую работу она сможет совершить. Так, более разреженный газ содержит меньше свободной энергии и больше связанной, чем сжатый газ при той же температуре. Следовательно, сжатый газ способен совершить больше полезной работы.
Величина непроизводительной, т. е. «обесцененной», части энергии D тем больше, чем меньше разность температур в системе. Мерой такого «обесценения» энергии является термодинамическая функция, зависящая от состояния системы и названная Клаузиусом энтропией (греческое — обращать внутрь). Эта функция обозначается в термодинамике буквой s.
Остановимся несколько подробнее на ее характеристике. Из анализа цикла Карно коэффициент полезного действия

| 1.54 |
В теории интегралов доказывается, что если интеграл по замкнутому контуру равен нулю, то подынтегральное выражение является полным дифференциалом некоторой функции от параметров, определяющих состояние системы. Можно записать
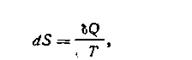
| 1.55 |
где S— функция состояния системы S = f{p, V, T, ...). Именно эта функция (S), введенная Клаузиусом (1850), и была названа энтропией.
Так как dS является полным дифференциалом, то изменение энтропии в каком-либо процессе зависит только от начального и конечного состояний и не зависит от пути перехода:
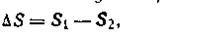
| 1.56 |
где ΔS — изменение энтропии при переходе системы из состояния (1) в состояние (2).
Это уравнение помогает оценить также и вероятность ожидаемого биологического процесса.
Если известно изменение энтропии системы и ее внешней среды, то возможно предсказание самопроизвольно протекающих процессов. Другими словами, для этого мы должны измерить и соотнести значения DSсистемы (DSc) и DSвнешней среды (DScp).
С учетом вышесказанного становится вполне очевидным, что если для данной системы
сумма DSс + DSср = 0, то система находится в состоянии равновесия;
если же сумма DSс + DSср > 0, то превращение может протекать даже самопроизвольно без дополнительного расходования энергии;
если же DSс + DSср < 0, то самопроизвольно процесс вообще не может протекать.
Выражение (I.53) является математической записью второго начала термодинамики для обратимых процессов. Подставляя в уравнение первого начала термодинамики вместо δQ равную величину TdS, получим аналитическое выражение первого и второго законов термодинамики для обратимых процессов:
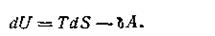
| 1.57 |
Наиболее просто изменение энтропии ΔS определяется для обратимых изотермических процессов. Для них из уравнений (I.54) вытекает, что
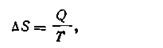
| 1.58 |
т. е. в обратимых изотермических процессах изменение энтропии равняется тепловому эффекту процесса, деленному на абсолютную температуру. Изменение энтропии рассчитывается на 1 моль и выражается в джоулях на градус. Единица измерения энтропии (так называемая «энтропийная единица», сокращенно э. е.) имеет следующее выражение:
1 э. е. = 1 Дж/(моль·К).
Так, при плавлении льда при 273,16 К поглощается теплота в количестве 6009,48 Дж/моль (мольная теплота плавления). Следовательно, изменение энтропии в этом процессе равно:
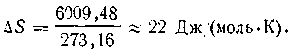
До сих пор, когда мы говорили об изменении энтропии, имелись в виду обратимые процессы; установлено, что величина ∆S для бесконечно мало обратимого процесса выражается уравнением (I.55). Однако, как мы уже знаем, обратимые процессы являются идеальными. Реальные же процессы, протекающие в природе, практически необратимы, так как при любых превращениях часть энергии переходит в теплоту, а последняя, как следует из второго начала термодинамики, может превращаться в другие виды энергии лишь частично.
На основании многочисленных опытов было установлено, чтово всяком необратимом процессе коэффициент полезного действия всегда меньше, чем в обратимом процессе, т. е.
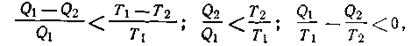
Из этого следует, что при необратимых процессах будет иметь место неравенство
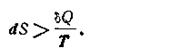
| 1.59 |
В системах изолированных, т. е. лишенных теплообмена с окружающей средой, процессы протекают без изменения тепловой энергии (δQ = 0). Поэтому в изолированных системах при изотермических и полностью обратимых процессах изменение энтропии (dS) равно нулю.
Если в замкнутых системах при Т = const и V = const будут идти необратимые процессы, энтропия этих систем будет возрастать.
В изолированных системах самопроизвольно могут протекать только процессы, которые сопровождаются увеличением энтропии. Это означает, что состояние устойчивого термодинамического равновесия в изолированной системе отвечает максимуму энтропии: ∆S = макс. Энтропия изолированной системы ни при каких условиях не может самопроизвольно убывать. Однако из всех предыдущих рассуждений нельзя сделать вывод о том, что процессы, протекающие с уменьшением энтропии, вообще невозможны. Дело в том, что подобные процессы в изолированных системах не могут возникать самопроизвольно, так как для их осуществления необходим определенный теплообмен с окружающей средой.
Для удобства запоминания все сказанное выше об энтропии представим схемой:

Уравнения первого и второго начал термодинамики, пригодные для обратимых и необратимых процессов, можно записать так:
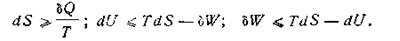
| 1.60 |
В этих уравнениях U и S не зависят от пути течения процесса. Работа W зависит от способа проведения процесса и будет максимальной, когда процесс полностью обратим. Эту максимальную работу обычно обозначают Wмакс. В необратимых процессах работа всегда меньше, т. е. W < Wмакс, поэтому отношение W/Wмакс≤1 может служить мерой необратимости.
Больцман и Гиббс показали, что энтропия есть некая средняя величина, которая является функцией неупорядоченности (хаотичности) движения множества молекул, т. е. имеет явно выраженный статистический характер.
Л. Больцман (1896) определил статистический смысл энтропии как логарифм вероятности существования системы
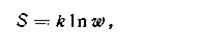
| 1.61 |
где ω — вероятность существования системы; k — постоянная Больцмана.
Количественной мерой термодинамической вероятности w является число различных микросостояний, которыми может быть осуществлено макросостояние, характеризуемое заданными термодинамическими параметрами.
Таким образом, в силу статистического характера второе начало неприменимо для системы с одной или малым числом частиц или молекул, т. е. для микрообъемов. Так, например, в газах вследствие хаотичности теплового движения молекул в отдельных микрообъемах плотность может кратковременно оказаться более высокой по сравнению со средней плотностью в макрообъеме. Это явление носит название флуктуации. Образование микроучастков с повышенной плотностью газа протекает самопроизвольно и с уменьшением энтропии, что не согласуется со вторым началом термодинамики. Аналогичные явления могут происходить и в отдельных микрообъемах растворов: концентрация частиц растворенного вещества на какой-то краткий период может оказаться в микрообъеме выше средней концентрации в макрообъеме.
Дата добавления: 2016-02-20; просмотров: 2022;
