Законом распределения случайной величины называется любое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Простейшей формой задания этого закона является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности.

Такая таблица называется рядом распределения случайной величины Х.

x_i	x₁	x₂	…..	x_n
p_i	p₁	p₂	…..	p_n

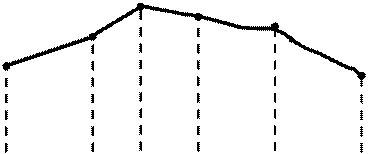
С целью наглядности ряд распределения представляют в графическом виде: по оси абсцисс откладываются возможные значения случайной величины, а по оси ординат их вероятности. В результате соединения полученных точек отрезками прямых, образуется многоугольник, который называется многоугольником распределения.

0 x₁x₂ x₃ x₄ x₅ x₆

Функция распределения

Закон распределения является полной и исчерпывающей характеристикой дискректной случайной величины. Однако она не является универсальной, так как не может быть применима к непрерывным случайным величинам. Непрерывная случайная величина принимает бесчисленное множество значений, заполняющих некоторый промежуток. Составить таблицу, включающую все значения непрерывной случайной величины практически невозможно. Следовательно, для непрерывной случайной величины не существует закон распределения, в том понимании как он существует для дискретной случайной величины.

Каким же образом описать непрерывную случайную величину?

Для этого используется не вероятность события Х=х, а вероятность события Х<х, где х - некоторая переменная. Вероятность этого события зависит от х и является функцией х.

Эта функция называется функцией распределения случайной величины Х и обозначается F(x):

F(x)=P(X<x)

Функция распределения является универсальной характеристикой случайной величины. Она существует для любых случайных величин: дискретных и непрерывных.

Свойства функции распределения:

1. При х₁>х₂ F(x₁)> F(x₂)

2. F(- ∞)=0

3. F(+ ∞)=1

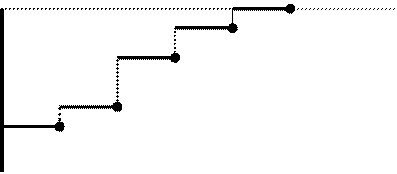
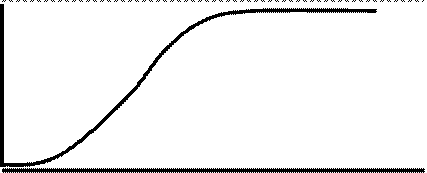
Функция распределения дискретной случайной величины - разрывная ступенчатя функция, скачки происходят в точках, соответствующих возможным значениям случайной величины, и равны вероятности этих значений. Сумма этих скачков равна единице.

1F(x)

1 F(x)

Числовые характеристики случайных величин.

Основными характеристиками дискретных случайных величин являются:

· функция распределения;

· ряд распределения;

для непрерывной случайной величины:

· функция распределения;

· плотность распределения.

Любой закон представляет некоторую функцию, и указание этой функции полностью описывает случайную величину.

Однако прирешении ряда практических задач не всегда необходимо характиризовать случайную величину в полном объеме. Достаточно указать только некоторые числовые параметры, характеризующие случайную величину.

Такие характеристики, назначение которых заключается в представлении в концентрированном виде наиболее существенных особенностей распределения, называются числовыми характеристиками случайной величины.

Характеристики положения

(МОЖ,мода,медиана)

Из всех используемых числовых характеристик случайных величин, чаще используются характеристики описывающие положение случайной величины на числовой оси, а именно указывают некоторое среднее значение, около которого группируются возможные значения случайной величины.

Для этого используются следующие характеристики:

· математическое ожидание;

· мода ;

· медиана.

Математическое ожидание (среднее значение) вычисляется следующим образом:

х₁р₁+х₂р₂+….+х_nр_n ∑ х_iр_i

М[Х] = = i=1

р₁ + р₂ + …..+р_n n

∑ p_i

i=1

N n

Учитывая, что∑ p_i_, МОЖ равно М[Х] = ∑ x_ip_i

i=1 i=1

Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений.

Приведенная формулировка справедлива только для дискретных случайных величин.

Для непрерывных величин

∞

М[Х] = ∫ x f(x)dx, где f(x) - плотность распределения Х.

- ∞

Существуют различные способы расчета среднего значения. Наиболее распространенными формами представления средних величин являются среднее арифметическое значение, медиана и мода.

Среднее арифметическое получается путем деления суммарной величины данного признака для всей однородной статистической совокупности на количество единиц этой совокупности. Для расчета среднего арифметического используется формула:

Хср = (Х1+Х2+... +Хn):n,

где Хi - значение признака у i-ой единицы совокупности, n - количество единиц совокупности.

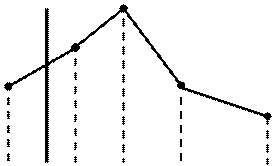
Модой случайной величины называется ее наиболее вероятное значение.

М

М

Медианой называется значение , которая расположена в середине упорядоченного ряда. Для нечетного количества единиц ряда медиана является единственной и находится точно в середине ряда, для четного - она определяется как среднее значение двух рядом расположенных единиц совокупности, занимающих среднее положение.

Статистикапредставляет собой отрасль науки, которая изучает количественную сторону массовых явлений общественной жизни, состоящих из отдельных элементов, единиц. Объединение элементов составляет статистическую совокупность. Целью изучения является установление количественных закономерностей развития данного явления. Оно основано на применении теории вероятностей и законе больших чисел. Сущность этого закона заключается в том, что несмотря на индивидуальные случайные колебания отдельных элементов совокупности, в общей массе проявляется определенная закономерность, характерная для данной совокупности в целом. Чем большее количество единичных элементов характеризующих исследуемое явление рассматривается, тем более четко обнаруживается закономерность, присущая данному явлению.

Преступность - явление социальное, массовое, представляет собой статистическую совокупность многочисленных фактов единичных преступных проявлений. Это и дает основание применять для ее изучения методы теории статистики.

В статистических исследованиях общественных явлений, можно выделить три этапа:

1) статистическое наблюдение, т.е. сбор первичного статистического материала;

2) сводная обработка собранных данных, в процессе которой производится подсчет итогов, расчет сводных (обобщающих) показателей и представление результатов в виде таблиц и графиков;

3)анализ, в ходе которого выявляются закономерности исследуемой статистической совокупности, взаимосвязи между различными ее составляющими, осуществляется содержательная интерпретация обобщающих показателей.

Первым этапом статистического исследования является статистическое наблюдение. Оно играет особую роль, так как ошибки, допущенные в процессе сбора данных, практически невозможно исправить на дальнейших этапах работы, что влечет за собой в конечном итоге неверные выводы о свойствах сследуемого явления, неправильную их интерпретацию.

По способу регистрации фактов статистическое наблюдение делится на непрерывное и прерывное. Под непрерывным, или текущим, понимается такое наблюдение, при котором установление и выявление фактов производится по мере их возникновения. При прерывном наблюдении регистрация фактов производится либо регулярно через определенные промежутки времени, либо по мере необходимости.

По охвату единиц обследуемой совокупности различают сплошное и несплошное наблюдение. Сплошным называется наблюдение, при котором учету подлежат все единицы изучаемой совокупности. Так, например, регистрация преступлений теоретически представляет собой сплошное наблюдение. Однако на практике определенная часть преступлений, называемых латентными, остается за пределами исследуемой статистической совокупности и поэтому фактически такое наблюдение является несплошным. Несплошным называется наблюдение, при котором регистрации подлежат не все единицы изучаемой совокупности. Оно подразделяется на несколько видов: наблюдение основного массива, выборочное наблюдение и некоторые другие.

Наблюдение основного массива (его иногда называют несовершенным сплошным методом) представляет собой такой вид несплошного наблюдения, при котором из всей совокупности единиц объекта наблюдению подвергается такая их часть, которая составляет подавляющую, преобладающую долю всей совокупности. Проведение наблюдения по этому методу практикуется в тех случаях, когда сплошной охват всех единиц совокупности сопряжен с особыми трудностями и в то же время исключение из наблюдения определенного количества единиц не оказывает существенного влияния на выводы о свойствах всей совокупности. Поэтому регистрацию преступлений скорее можно отнести именно к данному виду наблюдения.

Наиболее совершенным видом несплошного наблюдения является выборочное, при котором с целью характеристики всей совокупности обследованию подвергается лишь некоторая ее часть, однако взятая на выборку по определенным правилам. Основным условием правильности проведения выборочного наблюдения является такой отбор, в результате которого отобранная часть единиц по всем подлежащим изучению признакам достаточно точно характеризовала бы всю совокупность в целом. Чаще всего выборочное наблюдение применяется в ходе социологических исследований. В дальнейшем будем рассматиривать правила и способы отбора единиц при выборочном наблюдении.

После того как первичный материал собран и проверен, осуществляется второй этап статистического исследования сводка. Статистическое наблюдение дает материал, характеризующий отдельные единицы объекта исследования. Задача сводки - подытожить, систематизировать и обобщить результаты наблюдения так, чтобы стало возможным выявить характерные черты и существенные свойства, обнаружить закономерности изучаемых явлений и процессов.

Простейшим примером сводки является суммирование всех зарегистрированных преступлений. Однако такое обобщение не дает полного представления о всех свойствах криминогенной обстановки. Чтобы охарактеризовать преступность глубоко и всесторонне, необходимо знать, как общее количество преступлений распределяется по видам, времени, месту и способу совершения, и т.п.

Распределение единиц изучаемого объекта на однородные группы по существенным для них признакам называется статистической группировкой. Объекты, исследуемые статистикой, обычно характеризуются многими свойствами и отношениями, выражаемыми различными признаками. Поэтому группировка обследуемых объектов может производиться в зависимости от задач статистического исследования по одному или нескольким из этих признаков. Так, личный состав органа может быть сгруппирован по должностям, специальным званиям, возрасту, выслуге лет, семейному положению и т.д.

В результате обработки и систематизации первичных статистических материалов получаются ряды цифровых показателей, которые характеризуют отдельные стороны изучаемых явлений или процессов либо их изменение. Эти ряды называются статистическими. По своему содержанию статистические ряды делятся на два вида: ряды распределения и ряды динамики. Рядами распределения называются ряды, характеризующие распределение единиц исходной совокупности по какому-либо одному признаку, разновидности которого расположены в определенном порядке. Например, распределения общего количества преступлений на отдельные виды, численности всего личного состава по должностям представляют собой ряды распределения.

Динамическими рядами называются ряды, которые характеризуют изменение размеров общественных явлений во времени. Подробное рассмотрение таких рядов и их использование при аналихзе и прогнозе криминогенной обстановки составляет предметом отдельной лекции.

Результаты статистического наблюдения и сводки его материалов выражаются прежде всего в абсолютных величинах (показателях). Абсолютные величины показывают размеры общественного явления в данных условиях места и времени, например, количество совершенных преступлений или число лиц, их совершивших, фактическая численность личного состава или количество единиц автотранспорта. Абсолютные величины подразделяются на индивидуальные и суммарные (т.е. итоговые). Индивидуальными называются абсолютные величины, выражающие размеры количественных признаков у отдельных единиц той или иной совокупности объектов (например, число потерпевших или материальный ущерб по конкретному уголовному делу, возраст или выслуга лет данного сотрудника, его денежное содержание и т.п.). Они получаются непосредственно в процессе статистического наблюдения и фиксируются в первичных учетных документах. Индивидуальные абсолютные величины служат основой любого статистического исследования.

В отличие от индивидуальных суммарные абсолютные величины характеризуют итоговую величину признака по определенной совокупности объектов, охваченных статистическим наблюдением. Они получаются либо путем прямого подсчета числа единиц наблюдения (например, числа преступлений определенного вида), либо в результате суммирования значений признака у отдельных единиц совокупности (например, ущерб, нанесенный всеми преступлениями).

Однако абсолютные величины, взятые сами по себе, далеко не всегда дают надлежащее представление об изучаемых явлениях и процессах. Поэтому наряду с абсолютными величинами большое значение в статистике имеют относительные величины.

Сравнение является основным приемом оценки статистических данных и составной частью всех методов их анализа. Однако простое сопоставление двух величин недостаточно для точной оценки их соотношения. Это соотношение нужно также измерить. Роль меры такого соотношения и выполняют относительные величины.

В отличие от абсолютных, относительные величины представляют собой производные показатели. Они получаются не в результате простого суммирования, а путем относительного (кратного) сравнения между собой абсолютных величин.

В зависимости от характера изучаемого явления и конкретных задач исследования относительные величины могут иметь различную форму (внешний вид) выражения. Наиболее простой формой выражения относительной величины является число (целое или дробное), показывающее, во сколько раз одна величина больше другой, принятой за базу сравнения, или какую часть ее составляет.

Чаще всего, в аналитической деятельности органов внутренних дел применяется другая форма представления относительных чисел, процентное отношение, при которой основная величина принимается за 100. Для определения процентного отношения необходимо результат деления одной абсолютной величины на другую (базовую) умножить на 100.

Важная роль в сводной обработке статистических данных принадлежит средней величине. Поскольку каждая отдельно взятая единица статистической совокупности обладает индивидуальными особенностями, отличаясь от любой другой количественным значением, для характеристики свойств всей статистической совокупности в целом используется средняя величина. Под средней величиной в статистике понимают показатель, который отражает уровень меняющегося по величине признака в расчете на единицу однородной совокупности.

Для характеристики однородности статистической совокупности

по соответствующему признаку используются различные показатели: вариация, дисперсия, среднеквадратическое отклонение. Эти показатели позволяют оценить, в какой степени соответствующая средняя величина отражает свойства всей совокупности в целом, может ли она вообще использоваться в качестве обобщающей характеристики данной статистической совокупности. Подробное рассмотрение перечисленных показателей является самостоятельным вопросом.

Дата добавления: 2016-02-20; просмотров: 2457;