Основные этапы решения задач ИСО.

Постановка задачи – чрезвычайно ответственный этап ИСО. Первоначально задача формулируется заказчиком- оперирующей стороной. Такая постановка задачи обычно не бывает окончательной. Во время анализа исследуемой операции задача уточняется. Здесь роль исследователя состоит в проведении тщательного обследования объекта, формулировании цели операции, изучении множества факторов, влияющих на результаты. Исследователь операции совместно с заказчиком выделяет совокупность существенных факторов, и уточняет окончательную содержательную постановку задачи.

Построение математической модели. Представляет процесс формализации содержательной постановки задачи. В общем случае модели принятия решений сводятся к моделям задач математического программирования вида:

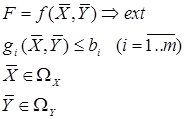(1)

где F- целевая функция (критерий эффективности операции),

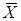- вектор контролируемых (управляемых) факторов,

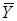- вектор неконтролируемых (неуправляемых) факторов,

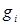-функция потребления i-того ресурса,

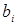- количество активных средств i-того ресурса.

Нахождение метода решения. Для нахождения оптимального решения 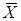_опт задачи (1) в зависимости от структуры целевой функции F и ограничений применяют те или иные методы теории мат. программирования:

1. Линейное программирование. 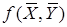, 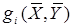- линейные функции относительно своих переменных 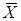и .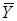

2. Нелинейное программирование, если хотя бы одна из 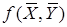, 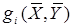- нелинейная.

3. Динамическое программирование, если 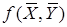явл. аддитивной (сепарабельной) или мультипликативной функцией своих аргументов.

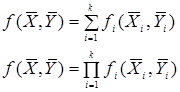
4. Дискретное (целочисленное) программирование, если на переменные 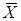и 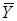наложено условие дискретности или целочисленности.

5. Геометрическое программирование, если целевая функция выражается соотношениям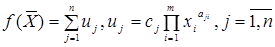и , или 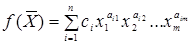, а ограничения 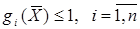. Здесь коэффициенты С_i и показатели степени а_ij являются произвольными константами, а независимые переменные х_j>0, j=1,m. Функции приведенного вида называются сигналами, а в случае х_j>0– позиномами.

6. Стохастическое программирование, если вектор 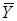- случайная величина, а целевая функция выражается мат. ожиданием. (Вместо 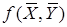рассматривают ).

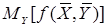7. Эвристическое программирование применяют для решения тех задач, в которых точный оптимум найти алгоритмическим путем невозможно из-за большой размерности исходной задачи или отсутствия методов решения. В таких случаях отказываются от поиска оптимального решения и отыскивают удовлетворительное с точки зрения практики решение. При этом пользуются специальными методами-эвристиками, основанными на опыте, знаниях и интуиции исследователя и позволяющими значительно сократить число просматриваемых планов.

Проверка и корректировка модели. В сложных системах ММ лишь частично отражает реальный процесс. Поэтому необходима проверка степени соответствия, или адекватности, между моделью и реальным объектом (процессом). Проверку производят сравнением предсказанного поведения на модели с фактическим (измеренным). Если их разница в пределах допустимого, то модель считается адекватной, в противном случае необходимо скорректировать модель. Корректировка может потребовать дополнительных исследований объекта, уточнения структуры модели. Четыре названных выше этапа повторяют многократно до тех пор, пока будет достигнуто удовлетворительное соответствие между выходом объекта и модели.

Реализация найденного решения на практике. Является важнейшим этапом, завершающим операционное исследование. Полученное решение в виде отчетов, инструкций и рекомендаций представляется заказчику. Опер. сторона принимает окончательное решение с учетом неформализуемой информации.

С точки зрения реализации оптимального решения на практике ИСО занимает особое место в проблематике АСУ различного назначения. Известно, что внедрение АСУ эффективно для решения таких задач управления, которые невозможно было решать при сложившейся ранее практике управления. Поэтому в настоящее время выдвинут т.н. принцип новых задач АСУ, под которым понимается поиск и постановка на производстве действительно новых задач оптимального управления, позволяющих создавать рентабельные АСУ.

ИСО является методологической основой для нахождения таких задач, разработки их моделей и алгоритмов решения, а также для практического внедрения оптимального решения.