Классическая транспортная задача. (КТЗ)
В настоящее время задачи транспортного типа или задача прикрепления поставщиков к потребителям стала типовой для промышленных предприятий, имеющих в своем составе несколько фирм, складов, оптовых баз и рынков сбыта. Эти задачи применяются для выбора оптимальных маршрутов доставки продукции от поставщиков к потребителям.
1.1 Постановка задачи. Имеются пункты производства 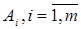 некоторой однородной продукции. В каждом пункте
некоторой однородной продукции. В каждом пункте 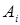 объем производства составляет
объем производства составляет 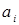 . Эта продукция поставляется в пункты потребления
. Эта продукция поставляется в пункты потребления 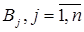 , причем потребность пункта
, причем потребность пункта 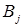 равна
равна 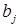 . Перевозка продукции возможна из любого пункта
. Перевозка продукции возможна из любого пункта 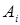 в любой пункт
в любой пункт 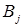 , при этом стоимость перевозки единицы продукции определяется величиной
, при этом стоимость перевозки единицы продукции определяется величиной 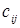 . Требуется найти такой план перевозки продукции, при котором запросы всех пунктов потребления будут полностью удовлетворяться, запасы продукции из всех пунктов производства полностью вывозиться, а суммарная стоимость перевозки была бы минимальной.
. Требуется найти такой план перевозки продукции, при котором запросы всех пунктов потребления будут полностью удовлетворяться, запасы продукции из всех пунктов производства полностью вывозиться, а суммарная стоимость перевозки была бы минимальной.
 Замечание. Очевидно, что при такой постановке решение задачи будет существовать только если выполняется условие баланса:
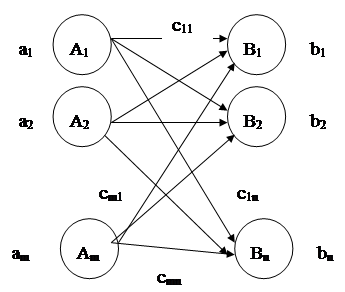
Замечание. Очевидно, что при такой постановке решение задачи будет существовать только если выполняется условие баланса: 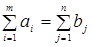 . Такая КТЗ называется закрытой.. Графическая интерпретация задачи представлена на рис.1.
. Такая КТЗ называется закрытой.. Графическая интерпретация задачи представлена на рис.1.
1.2Математическая модель КТЗ.
Пусть  - количество продукции, перевезенной из пункта Аi в Bj. Тогда ММ КТЗ запишется в виде:
- количество продукции, перевезенной из пункта Аi в Bj. Тогда ММ КТЗ запишется в виде:
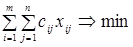 (1)
(1)
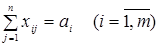 (2)
(2)
 (3)
(3)
 (4)
(4)
Здесь целевая функция (1) отражает суммарные транспортные расходы. Ограничения (2) требуют, чтобы вся продукция была вывезена, а ограничения (3) – чтобы потребности всех пунктов потребления были удовлетворены. Условие (4) вытекает из физического смысла введенных переменных.
Ограничения (2)-(4) задают планы перевозок (хij)mxn. Т.О., ММ КТЗ относится к классу ЗЛП. В этой задаче 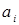 - активные средства,
- активные средства, 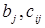 - определенные (фиксированные) неконтролируемые факторы, а матрица плана перевозок
- определенные (фиксированные) неконтролируемые факторы, а матрица плана перевозок  - стратегии оперирующей стороны. Цель операции задается целевой функцией (1). Если некоторая матрица
- стратегии оперирующей стороны. Цель операции задается целевой функцией (1). Если некоторая матрица 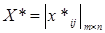 является решением ЗЛП (1)-(4), то она является оптимальной (наилучшей) стратегией оперирующей стороны. Т.к. КТЗ относится к классу ЗЛП, то она может быть решена стандартными методами ЛП. Однако, учитывая особенности КТЗ, можно модифицировать общие алгоритмы решения ЗЛП таким образом, чтобы получить более эффективные алгоритмы. Для решения КТЗ используется алгоритм, разработанный в соответствии с методом потенциалов.
является решением ЗЛП (1)-(4), то она является оптимальной (наилучшей) стратегией оперирующей стороны. Т.к. КТЗ относится к классу ЗЛП, то она может быть решена стандартными методами ЛП. Однако, учитывая особенности КТЗ, можно модифицировать общие алгоритмы решения ЗЛП таким образом, чтобы получить более эффективные алгоритмы. Для решения КТЗ используется алгоритм, разработанный в соответствии с методом потенциалов.
Дата добавления: 2016-02-20; просмотров: 941;
