Уровень обслуживания клиентов и страховой запас
Обеспечение необходимого уровня обслуживания клиентов (потребителей) является основной целью формирования и поддержания запаса. Без установления этого уровня невозможно определить необходимый размер этого запаса.
Уровень обслуживания клиента (УОК) в отношении к управлению запасами можно определить двояко:
1. Как вероятность отсутствия недостатка запасов в цикле пополнения запаса (УOК1);
2. Как долю реализованных заказов в цикле пополнения запасов (УOK2).
Оба показателя выражаются в процентах. Например:
· УОК1 = 95% означает, что вероятность события «в данном цикле пополнения запаса весь прогнозируемый спрос будет удовлетворен» составляет 0,95. Или иначе - риск появления недостатка в запасе составляет 0,05.
· УОК2 = 95% означает, что в данном цикле пополнения запаса будет удовлетворено 95% спроса, т.е. если спрос в данном цикле составил 1000 единиц, то из запаса обеспечено 950 единиц.
На практике для конкретного ассортимента используется один из показателей уровня обслуживания клиентов. Выбор показателя должен основываться на характеристиках товара, его назначении, а также последствиях, связанных с появлением недостатка в запасах.
Уровень обслуживания клиентов, понимаемый как вероятность появления недостатка (УOK1) используется в тех случаях, когда важен не столько размер недостающего запаса, а сам факт появления недостатка запасов. Это касается материально-технического снабжения производства, снабжения запасными частями, а также таких поставок, где важно не потерять клиента (например, клиента группы А).
Уровень обслуживания клиентов, понимаемый как уровень количественного удовлетворения спроса (УOK2) имеет значение там, где на результат деятельности влияет каждый реализованный заказ, например в торговле и распределении, где каждая недостача в запасах приводит к потере дохода от товарооборота.
Представленные ниже примеры основаны на следующей модели пополнения запаса: когда уровень запаса достигнет определенного уровня, размещается заказ на равные партии товаров. Поставка осуществляется в заказанном размере через определенный промежуток времени Т (длительность цикла пополнения).
В таблице 4.10 и на рисунке 4.14 представлены данные о частоте спроса на CD диски в цикле пополнения запаса, который составляет 2 дня. Данные представлены по результатам 78 наблюдений. Размер поставки составляет 500 дисков. Заказ осуществляется, когда уровень запаса составит 60 штук. Необходимо определить показатели уровня обслуживания клиентов.
Таблица 2.10. Распределение частоты спроса на CD диски
| Интервалы размера спроса | |||||||||||||
| 15-19 | 20-24 | 25-29 | 30-34 | 35-39 | 40-44 | 45-49 | 50-54 | 55-59 | 60-64 | 65-69 | 70-74 | 75-79 | 80-84 |
Рисунок 4.14. Эмпирическое распределение спроса на CD диски
Число периодов, в которых спрос превышал 60 единиц: 7+5+4+2+1=19
Число всех периодов: 78
Вероятность появления недостатка запасов 19/78=0,244
УOK1=1-0,244=75,6%
Спрос будет находиться в интервале (60-64) с вероятностью 7 / 78 = 0,0897. Для упрощения примем, что эта цифра соответствует вероятности спроса q1 - 62 штуки (середина интервала 60-64). При таком спросе размер неудовлетворенного спроса составит x1 = 62 - 60 = 2 единицы. Аналогично рассчитаем для остальных интервалов:
| i | Интервал спроса | qi (середина интервала) | Число недостающих единиц qi-60 | Вероятность |
| (60-64) | 7 / 78 = 0,0897 | |||
| (65-69) | 5 / 78 = 0,0641 | |||
| (70-74) | 4 / 78 = 0,0513 | |||
| (75-79) | 2 / 78 = 0,0256 | |||
| (80-84) | 1 / 78 = 0,0128 |
Ожидаемое число недостач:
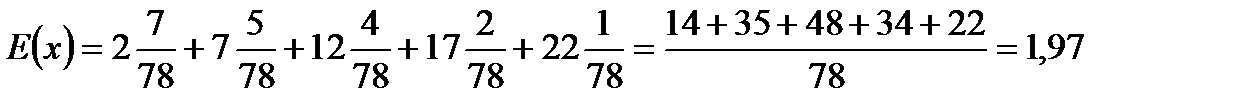
Это означает, что ожидаемое число недостач в запасе, приходящихся на один цикл пополнения запаса составляет 1,97 дисков.
Если поставка равна 500 штук (в этом случае это означает, что она покрывает потребность чуть более чем 20 дней) то 500-1,97 = 498,03.
Уровень обслуживания клиентов, как доля реализованных заказов:
УOK2 = 498,03 / 500 = 0,9961 = 99,6%
Для данных из примера определим УOK1 и УOK2 приняв, что распределение спроса подчинено нормальному закону распределения, используя параметры этого распределения (рис. 4.15).
Рисунок 4.15. Использование нормального распределения для описания эмпирического распределения спроса на CD диски
Для данного примера средний размер спроса в цикле пополнения составляет 48,3, или около 24,15 диска в день, а стандартное отклонение длительности цикла пополнения составляет σqT = 15,05.
Расчет УOK1. Определим отклонение спроса в размере 60 единиц (размер запасов в момент осуществления заказа) от среднего спроса в цикле пополнения запаса, равного 48,3 единицы в стандартных отклонениях спроса в цикле пополнения.
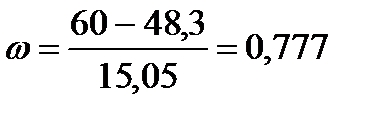
Из таблицы A приложения 2 определяем УОK1 ≈ 78%.
Точный размер УОK1 можно рассчитать, используя, например, Excel.
НОРМСТРАСП (0,777) = 0,781 (78,1%)
Расчет УOK2. Для рассчитанного коэффициента ω = 0,777 из таблицы С приложения 2 значение показателя I(ω)≈0,12 (так называемое стандартизированное число недостач). Далее определяем ожидаемое число недостач в запасе для одного цикла пополнения:
чн = I(ω)·σqT = 0,12·15,05 = 1,806
Так как средний размер партии равен 500 штук, то
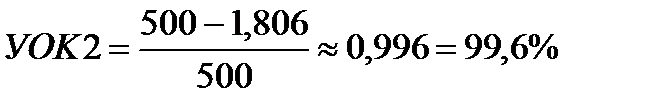
В представленных ниже примерах показана взаимосвязь между УOK1 и УOK2.
Средний спрос в неделю на маргарин M оптового предприятия составляет 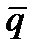 =1460 упаковок при стандартном отклонении σT = 480. Спрос в рассматриваемом периоде не имеет сезонности и тренда. Размер поставки составляет 6300 упаковок, а длительность цикла пополнения запасов – 1 неделя. Владелец оптового предприятия планирует допустить 2% нереализованного спроса в году. Используемая информационная система позволяет определять уровень обслуживания клиентов по показателю УOK1. Какой размер данного показателя следует принять в системе, чтобы удовлетворить установленный уровень реализации спроса?
=1460 упаковок при стандартном отклонении σT = 480. Спрос в рассматриваемом периоде не имеет сезонности и тренда. Размер поставки составляет 6300 упаковок, а длительность цикла пополнения запасов – 1 неделя. Владелец оптового предприятия планирует допустить 2% нереализованного спроса в году. Используемая информационная система позволяет определять уровень обслуживания клиентов по показателю УOK1. Какой размер данного показателя следует принять в системе, чтобы удовлетворить установленный уровень реализации спроса?
Допустимый уровень нереализованного спроса равный 2%, означает установление второго показателя уровня обслуживания на уровне УOK2 = 98%.
Годовой спрос на складе М можно рассчитать как Qгод= 1460·52 = 75920 упаковок. Это означает, что число поставок в году:
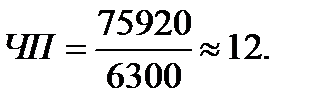
Допустимое число недостач в течение года, в соответствии с принятой стратегией (УOK2 = 98%) составляет:
ЧН = 0,02·75920 = 1518,4 упаковок
Допустимое число недостач на один цикл пополнения запаса составляет:
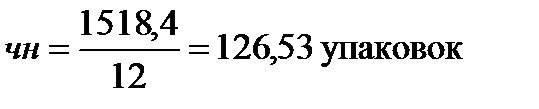
Стандартное отклонение спроса в цикле пополнения запаса:
σqT = σq 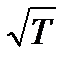 = 480
= 480 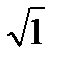 =480 штук
=480 штук
Определяем стандартизированное число недостач:
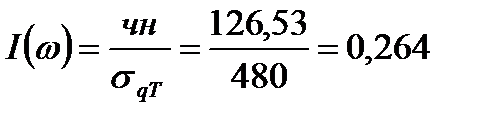
Из таблицы С приложения 2 находим ω ≈ 0,3, а отсюда УОК1 ≈ 61,8%
Какого действительного уровня реализации заказов (размер УOK2) следует ожидать, если в ситуации, описанной в примере, в информационную систему будет ошибочно введен размер показателя УOK2 (98%) как УOK1?
Если в систему ввести УOK1=98%,это означает принятие коэффициента безопасности ω = 2,054, тогда стандартизированное число недостач равно I(ω) ≈0,074(путем подбора на основе таблицы С приложения 2).
Зная стандартное отклонение спроса в цикле пополнения запаса (σqT= 480) рассчитаем ожидаемое число недостач, приходящихся на один цикл:
чн = I(ω)·σйT = 0,074·480 = 35,53
Отсюда ожидаемая годовая сумма недостач:
ЧН = чп·чн = 12·35,53 = 426,24
Ожидаемый уровень обслуживания УOK2, в соответствии с прогнозируемым размером годового спроса Qгод = 75920 упаковок составит:
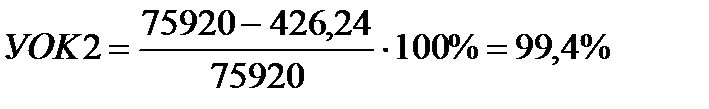
Это значительно больше, чем запланировал собственник. С этим не было бы проблемы, если бы не факт, что это будет достигнуто ценой значительно большего, чем требуется размера страхового запаса.
Расчет страхового запаса. Для расчета необходимого размера страхового запаса требуется следующая информация:
1. Стандартное отклонение ошибки прогнозируемого спроса в цикле пополнения запаса σqT.
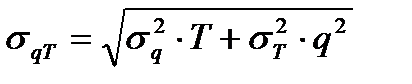
Для этого необходимо знать: средний размер спроса 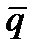 ; стандартное отклонение ошибки прогноза σq; ожидаемую длительность цикла пополнения запаса Т, стандартное отклонение длительности цикла пополнения запаса σT;
; стандартное отклонение ошибки прогноза σq; ожидаемую длительность цикла пополнения запаса Т, стандартное отклонение длительности цикла пополнения запаса σT;
2. Требуемый уровень обслуживания клиентов (УОК1 или УОК2). Его можно определить на основании: опыта, сравнения с конкурентами (бенчмаркинг), определённых требований потребителей, оптимизационного расчета, если известны издержки хранения запаса и издержки недостатка запасов.
3. Принятую систему управления запасами – с непрерывным или периодическим контролем состояния запасов.
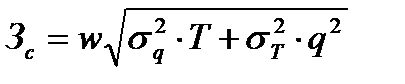 После того как эти данные получены, можно рассчитать требуемый страховой запаспо следующей формуле:
После того как эти данные получены, можно рассчитать требуемый страховой запаспо следующей формуле:
Рассмотрим следующий пример. По данным за год, средний недельный спрос на определенный тип винтов, применяемых как соединительный элемент в монтаже группы механических устройств, имеет стационарный характер и подчинен нормальному закону распределения со средней 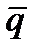 =1250 штук и стандартным отклонением σq=325 штук. Учитывая массовый характер расхода эти винты содержатся в запасе, пополняемом периодическими закупками у производителя. Заказ (обычно 10000 штук) реализуется в течение 1 недели, срок доставки всегда выдерживается. Допустимый риск появления недостатка в запасе установили на уровне 5%. Необходимо запланировать уровень страхового запаса на очередной период.
=1250 штук и стандартным отклонением σq=325 штук. Учитывая массовый характер расхода эти винты содержатся в запасе, пополняемом периодическими закупками у производителя. Заказ (обычно 10000 штук) реализуется в течение 1 недели, срок доставки всегда выдерживается. Допустимый риск появления недостатка в запасе установили на уровне 5%. Необходимо запланировать уровень страхового запаса на очередной период.
В соответствии со стационарностью спроса (то есть равномерным распределением спроса во времени) средний размер спроса, рассчитанный на основании прошлогодних данных, является единственно обоснованным прогнозом на следующий год. В этой ситуации стандартное отклонение ошибки прогноза еженедельного спроса равно простому стандартному отклонению спроса (от среднего): σq= 325
Из-за отсутствия информации об изменчивости длительности цикла пополнения запаса, принимаем σт ≈ 0. Следовательно, стандартное отклонение ошибки прогноза в цикле пополнения запаса равно:
σqT=σq 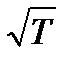 =325
=325 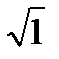 =325
=325
Для определения размера страхового запаса необходимо также определить требуемый уровень обслуживания клиентов. В соответствии с представленной информацией, используется показатель УОК1= 95%. Из таблицы В приложения 2 размер показателя безопасности w = w (УОК1= 95%) = 1,645. Размер коэффициента можно также определить используя стандартную функцию Excel. w = НОРМСТРАСП (УОК1).
Размер страхового запаса должен составлять:
Зс = w • σqT= 1,645 • 325 ≈ 535 единиц (результат вычислений страхового запаса необходимо округлять до целых в большую сторону).
Рассмотрим, как необходимо изменить страховой запас для данных из примера, если длительность цикла пополнения запаса увеличится в два раза, до Т = 2 недели.
Стандартное отклонение ошибки прогноза в цикле пополнения запаса тогда составит:
σqT = σq 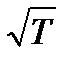 =325
=325 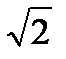 =459,6,
=459,6,
а новый размер страхового запаса:
Зс = w • σqT = 1,645 • 459,6 ≈ 756 единиц
Как необходимо изменить страховой запас для данных из примера, если длительность цикла пополнения запаса будет варьировать со стандартным отклонением σT =0,5 недели.
Стандартное отклонение ошибки прогноза в цикле пополнения запаса тогда равно:
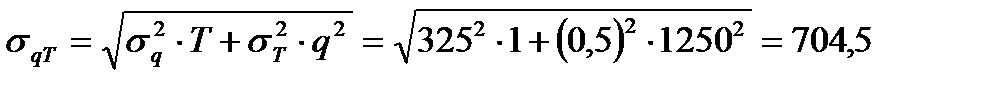
а размер страхового запаса:
Зс = w • σqT = 1,645 • 704,5 ≈ 1159 единиц
Отсюда заметно, что с виду небольшая изменчивость длительности цикла пополнения запаса (приблизительно один раз на 6 циклов поставок это время составляет 1,5 недели) вызвало необходимость поддержания значительно большего размера страхового запаса чем при двукратном удлинении средней длительности этого цикла.
А теперь проверим, в какой степени снизится уровень обслуживания клиентов, если, не смотря на изменчивость длительности Т, сохраним страховой запас на уровне 535 единиц.
В данном случае для вычислений необходимо принять σqT =704,5 единиц. Для определения действительного уровня обслуживания клиентов определим действительное значение коэффициента безопасности:
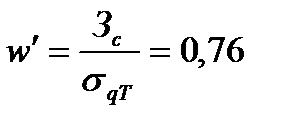
Из таблицы или функции НОРМСТРАСП(w') определим УОК1' = 77,6 %. Недостаток запаса, вместо планируемой допустимой частоты (в среднем раз на двадцать доставок), будет случаться намного чаще – приблизительно в каждой четвёртой поставке.
Оптимизация уровня обслуживания клиентов и размера страхового запаса. Располагая данными об издержках, связанных с появлением недостатка запаса, можно попытаться оптимизировать уровень обслуживания клиентов, а затем и размер страхового запаса.
Допустим, что в рассмотренном выше примере дополнительно известно, что стоимость 1 винта составляет 8 у.е., а доля издержек, связанных с содержанием запаса M=0,2. Примем также, что в случае возникновения недостатка запасов возникает необходимость срочного их пополнения, что вызывает дополнительные издержки в размере 800 у.е. Рассчитаем оптимальный уровень обслуживания, обеспечивающий минимальные общие издержки поддержания страхового запаса и издержек, связанных с возникновением недостатка запасов.
Рассмотрим часть общих издержек, связанных с принятым уровнем обслуживания клиентов:
ИЗУОК = ИССЗпер. + ИНЗ.
ИССЗпер. = M∙C∙Зс,
где M – доля издержек, связанных с содержанием запаса (в примере M = 0,2);
С – цена единицы изделия в запасе (в примере С = 8 у.е.);
Зс – размер страхового запаса в натуральном выражении.
ИНЗ = (1-УОК1)∙ДИ∙чп,
где ДИ – дополнительные издержки, связанные с возникновением недостатка запасов в цикле пополнения (в примере ДИ = 800 у.е.);
чп – число поставок в анализируемом периоде (в примере: годовой спрос = 1250 (штук в неделю) ∙ 52 (число недель в году) = 65000; размер партии – 10000; чп=65000/10000=6,5).
В таблице 4.11 представлены расчеты составляющей общих издержек, связанных с принятым уровнем обслуживания клиентов (ИЗУОК) для различных значений УОК1:
- ожидаемые издержки, связанные с недостатком запасов в анализируемом периоде (в данном случае в течение года) = ожидаемая сумма недостатка запаса в одном цикле пополнения ∙ число циклов пополнения в анализируемом периоде;
- ожидаемая сумма недостатка запасов в одном цикле пополнения = вероятность возникновения недостатка ∙ постоянные издержки, связанные с возникновением недостатка запасов.
Таблица 4.11. Оптимизация уровня обслуживания клиентов для данных из примера
| УОК1 | Вероятность возникновения недостатка запасов | ИНЗ | w | Размер страхового запаса | ИССЗпер. | ИЗУОК |
| 85% | 0,15 | 1,036 | 539,2 | 1319,2 | ||
| 86% | 0,14 | 1,080 | 561,6 | 1289,6 | ||
| 87% | 0,13 | 1,126 | 585,6 | 1261,6 | ||
| 88% | 0,12 | 1,175 | 611,2 | 1235,2 | ||
| 89% | 0,11 | 1,227 | 638,4 | 1210,4 | ||
| 90% | 0,10 | 1,282 | 667,2 | 1187,2 | ||
| 91% | 0,09 | 1,341 | 697,6 | 1165,6 | ||
| 92% | 0,08 | 1,405 | 731,2 | 1147,2 | ||
| 93% | 0,07 | 1,476 | 768,0 | 1132,0 | ||
| 94% | 0,06 | 1,555 | 808,0 | 1120,0 | ||
| 95% | 0,05 | 260 | 1,645 | 535 | 856,0 | 1116,0 |
| 96% | 0,04 | 1,751 | 910,4 | 1118,4 | ||
| 97% | 0,03 | 1,881 | 977,6 | 1133,6 | ||
| 98% | 0,02 | 2,054 | 1067,2 | 1171,2 | ||
| 99% | 0,01 | 2,326 | 1209,6 | 1261,6 |
Вероятность возникновения недостатка запасов в цикле пополнения можно определить как 1-УОК1. Если УОК1=85%, то это означает, что вероятность возникновения недостатка запасов в цикле пополнения равна 0,15, а издержки, связанные с недостатком запасов можно определить следующим образом:
ИНЗ = (1-УОК1)∙ДИ∙чп=(1-0,85)∙800∙6,5=780 у.е.
Как видно по данным таблицы 4.11, общая сумма издержек, связанных с содержанием страхового запаса и издержек, связанных с возникновением недостатка запасов достигает минимума для УОК1≈95%.
Дата добавления: 2016-02-20; просмотров: 3574;
