Анализ и прогнозирование спроса
Анализ спроса на товар по конкретной ассортиментной позиции является исходным пунктом выбора методов управления его запасами.
К основным методам анализа спроса относятся: АВС – анализ, XYZ – анализ, анализ профиля спроса и подбор теоретического закона распределения, анализ тренда и сезонности спроса.
АВС – анализ. Около ста лет назад итальянский экономист Вильфредо Парето провел ряд исследований распределения доходов в Италии. И обнаружил, что 80% дохода компании приносят 20% ее персонала. Продолжив исследования, ученые обнаружили, что, как правило, 80% результата любого процесса обеспечиваются 20% участвующими в этом процессе факторами.
В результате появилось правило «80:20»: 80% выручки обеспечивают 20% торгового персонала; 80% выручки приносят 20% ваших покупателей; 80% продаж из запасов происходит по 20% товарных позиций.
В процессе ABC – классификации, товары, приносящие 80% выручки, обычно получают ранг А. Он может быть присвоен 5, 10 или 20% товарных позиций.
Остальные товары, приносящие 20% выручки, обычно ранжируются так: 15% выручки – ранг В; 5% выручки – ранг С.
Алгоритм проведения АВС – классификации представлен в следующем примере. Таблица 4.2 содержит список товаров, проданных в течение года. Возле кода товара, в таблице содержится цена за единицу, число проданных единиц и общий товарооборот. Необходимо определить группы А, B и C.
Таблица 4.2. Исходные данные для ABC - анализа
| A | B | C | D | E |
| № | Код товара | Цена за единицу, у.е. | Количество проданных единиц | Товарооборот, у.е. |
| 1. | KK001 | |||
| 2. | KK002 | |||
| 3. | KK003 | |||
| 4. | KK004 | |||
| 5. | KK005 | |||
| 6. | KK006 | |||
| 7. | KK007 | |||
| 8. | KK008 | |||
| 9. | KK009 | |||
| 10. | KK010 | |||
| 11. | KL001 | |||
| 12. | KL002 | |||
| 13. | KL003 | |||
| 14. | KL004 | |||
| 15. | KL005 | |||
| 16. | KL006 | |||
| 17. | KL007 | |||
| 18. | KL008 | |||
| 19. | KL009 | |||
| 20. | KL010 | |||
| 21. | KM001 | |||
| 22. | KM002 | |||
| 23. | KM003 | |||
| 24. | KM004 | |||
| 25. | KM005 | |||
| 26. | KM006 | |||
| 27. | KM007 | |||
| 28. | KM008 | |||
| 29. | KM009 | |||
| 30. | KM010 | |||
| 31. | KN001 | |||
| 32. | KN002 | |||
| 33. | KN003 | |||
| 34. | KN004 | |||
| 35. | KN005 | |||
| 36. | KN006 | |||
| 37. | KN007 | |||
| 38. | KN008 | |||
| 39. | KN009 | |||
| 40. | KN010 |
Чтобы выделить группы A, B и C, действуем следующим образом:
1. Колонки B, C, D и E сортируем по убыванию в соответствии со значением колонки E («Товарооборот»). Если данные размещены в таблице Microsoft Excel, можно использовать его стандартные функции.
2. Определяем общую сумму товарооборота для всех указанных позиций. В данном случае она равна 2767682 у.е.
3. Вводим колонку F, в которой по каждой позиции определяем ее долю в общем товарообороте.
4. Вводим колонку G, в которой суммируем нарастающим итогом долю, вычисленную в колонке F.
5. Как группу A выделяем позиции, нарастающая сумма которых в общем товарообороте ограничена 80%, для группы B - 95%, остальные позиции - относим к группе C. В таблице 4.3 показаны данные после выполнения всех указанных шагов.
Таблица 4.3. Таблица 4.2, преобразованная в соответствии с последовательностью ABC анализа
| A | B | C | D | E | F | G | Группа |
| № | Код товара | Цена за единицу, у.е. | Количество проданных единиц | Товарооборот, у.е. | Доля в товарообороте, % | Доля в товарообороте нарастающим итогом, % | |
| 1. | KK003 | 21,0 | 21,0 | A | |||
| 2. | KL002 | 15,0 | 35,9 | A | |||
| 3. | KM006 | 11,0 | 46,9 | A | |||
| 4. | KM009 | 9,0 | 55,9 | A | |||
| 5. | KN001 | 8,0 | 64,0 | A | |||
| 6. | KM010 | 7,0 | 71,0 | A | |||
| 7. | KL008 | 5,0 | 76,0 | A | |||
| 8. | KN002 | 4,0 | 79,9 | A | |||
| 9. | KM005 | 3,1 | 83,0 | B | |||
| 10. | KM004 | 2,1 | 85,1 | B | |||
| 11. | KM002 | 1,8 | 86,9 | B | |||
| 12. | KK004 | 1,5 | 88,5 | B | |||
| 13. | KM001 | 1,2 | 89,6 | B | |||
| 14. | KL006 | 1,0 | 90,6 | B | |||
| 15. | KL010 | 0,9 | 91,5 | B | |||
| 16. | KK010 | 0,8 | 92,4 | B | |||
| 17. | KK007 | 0,8 | 93,2 | B | |||
| 18. | KL005 | 0,7 | 93,9 | B | |||
| 19. | KM008 | 0,6 | 94,5 | B | |||
| 20. | KL001 | 0,5 | 95,0 | B | |||
| 21. | KL007 | 0,5 | 95,4 | C | |||
| 22. | KM003 | 0,5 | 95,9 | C | |||
| 23. | KN007 | 0,4 | 96,3 | C | |||
| 24. | KK001 | 0,4 | 96,7 | C | |||
| 25. | KN009 | 0,4 | 97,1 | C | |||
| 26. | KN010 | 0,4 | 97,5 | C | |||
| 27. | KN008 | 0,4 | 97,9 | C | |||
| 28. | KK008 | 0,3 | 98,2 | C | |||
| 29. | KN004 | 0,3 | 98,5 | C | |||
| 30. | KN005 | 0,3 | 98,8 | C | |||
| 31. | KN006 | 0,2 | 99,0 | C | |||
| 32. | KL009 | 0,2 | 99,2 | C | |||
| 33. | KK005 | 0,2 | 99,4 | C | |||
| 34. | KL004 | 0,1 | 99,5 | C | |||
| 35. | KK006 | 0,1 | 99,6 | C | |||
| 36. | KL003 | 0,1 | 99,8 | C | |||
| 37. | KK009 | 0,1 | 99,9 | C | |||
| 38. | KN003 | 0,1 | 99,9 | C | |||
| 39. | KK002 | 0,0 | 100,0 | C | |||
| 40. | KM007 | 0,0 | 100,0 | C | |||
Результаты, полученные после преобразования данных и представленные в таблице 4.3 можно проиллюстрировать графически в виде кривой Лоренца. Она показана на рисунке 4.3. По оси Х откладывается нарастающая доля числа товарных позиций в общем их количестве, а по оси Y – соответствующая им нарастающая доля в общем товарообороте.
| А |
| В |
| С |
Следует помнить, что ABC - классификация не делит материалы или товары на важные, менее важные и незначительные. Часто в группе С будут дешевые изделия без которых, однако не возможно обойтись. ABC - классификация помогает скорее выделить позиции имеющие большую долю в объеме продаж или расхода, что важно и с точки зрения управленияих запасами, так как эти запасы будут наиболее дорогими.
Достаточно ли для принятия решений, связанных с содержанием запасов только данной классификации? Обратим внимание на две позиции, отнесенные к группе А: KL002 и KN001. Можно заметить, что, несмотря на то, что эти позиции находятся рядом по доле в общем объеме товарооборота, причина такого положения разная. Недорогих изделий KL002 продано 82901 штука, а дорогих изделий KN001 - только 707 штук. Изделие KL002 находитсяв группе A благодаря большому обороту, а KN001 благодаря высокой цене. Данные размышления хорошо иллюстрирует рисунок 4.4, представляющий «карту» группы в координатах «цена – количество».
Похожее распределение также можно осуществить в группе B и в группе C. Отсюда следует, что кроме товарооборота следует учитывать количество проданных товаров. Классификация по такому критерию называется XYZ – классификацией или XYZ - анализом.
XYZ – анализ. Основным признаком классификации XYZ является характер спроса (продаж): товары, продаваемые в больших количествах, имеющие массовый характер спроса – группа X; товары, потребляемые в средних размерах (в количественном выражении) – группа Y; товары, продаваемые нерегулярно, разово – группа Z.
| KN001 |
| KM009 |
| KN002 |
| KK003 |
| KL002 |
Рисунок 4.4.Распределение «цена-количество» для ассортиментных позиций группы А
Если известны данные за несколько периодов (дней, месяцев, кварталов) в соответствии с XYZ – классификацией весь ассортимент (ресурсы) делят на три группы в зависимости от степени равномерности спроса и точности прогнозирования следующим образом:
- в группу Х включают товары, спрос на которые равномерен, либо подвержен незначительным колебаниям. Объем реализации по товарам, включенным в данную группу, хорошо предсказуем.
- в группу Y включают товары, которые потребляются в колеблющихся объемах. В частности, в эту группу могут быть включены товары с сезонным характером спроса. Возможности прогнозирования спроса по товарам группы Y — средние.
- в группу Z включают товары, спрос на которые возникает лишь эпизодически. Прогнозировать объемы реализации товаров группы Z сложно.
Признаком, на основе которого конкретную позицию ассортимента относят к группе Х, Y или Z, может быть коэффициент вариации спроса по этой позиции:
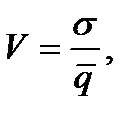
где V – коэффициент вариации спроса;
σ – стандартное отклонение спроса за анализируемый период;
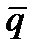 - средний спрос в единицу времени (день, неделя, месяц) за анализируемый период.
- средний спрос в единицу времени (день, неделя, месяц) за анализируемый период.
Стандартное отклонение спроса определяется по формуле:
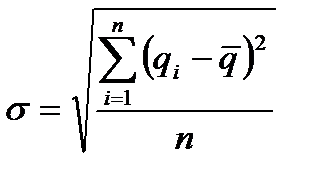
где qi – спрос в единицу времени (день, неделю, месяц);
n – число анализируемых периодов.
Возможный алгоритм дифференциации ассортимента на группы XYZ: X – V<10%; Y – 10%≤V<25%; Z – 25%≤V
Наложением результатов XYZ–анализа на данные ABC-метода получаем 9 групп ресурсов, для каждой из которых необходимо выбрать соответствующий метод управления запасами.
Группы AX, AY и AZ требуют наибольшего внимания с логистической точки зрения, для них необходимо тщательное планирование потребности, нормирование расхода, ежедневный учет и контроль, постоянный анализ отклонений от запланированных показателей. Причем для категории AX следует рассчитывать оптимальный размер закупок и использовать технологию поставок JIT (Just in Time - точно в срок). А для категории AZ эффективнее использовать систему снабжения по запросам с обязательным расчетом величины страхового запаса
Анализ профиля спроса и подбор теоретического закона распределения. Очень важно уметь определять профиль спроса, который является основой выбора одного из основных теоретических распределений частоты. Рассмотрим, как часто встречались отдельные размеры продаж на некоторые товары, отнесенные к категории A из таблицы 4.3.
Рассмотрим продажи изделия KM009 за один квартал (для ограничения числа рассматриваемых данных). В таблице 4.4 указана величина спроса (количественно) по дням квартала. Определим профиль спроса на данное изделие.
Таблица 4.4. Спрос на изделие KM009 по дням квартала
| Дни недели | Недели квартала | ||||||||||||
| Понедельник | |||||||||||||
| Вторник | |||||||||||||
| Среда | |||||||||||||
| Четверг | |||||||||||||
| Пятница | |||||||||||||
| Суббота |
Рисунок 4.5 иллюстрирует графически изменение спроса за рассматриваемый отрезок времени
Определение частоты отдельных значений количества можно выполнить с помощью Excel (используя функцию СЧЁТЕСЛИ). Результат такого анализа выполненного по данным таблицы 4.4 представлен на рисунке 4.6. Полученное распределение называется экспериментальным (эмпирическим), так как является результатом непосредственного анализа экспериментальных данных.
Часто более удобно и практически приемлемо определять профиль спроса на основе еженедельных данных. Особенно это касается товаров со значительным размером оборота, например KL002 из примера.
Рисунок. 4.5. Графическое представление данных из таблицы 5.4.
Рисунок 4.6. Распределение размеров продаж изделия KM009
В таблице 4.5 представлен еженедельный спрос на изделие KL002 из примера. Установить эмпирическое распределение частоты спроса и представить его профиль. Ограничить число значений посредством агрегации данных.
Анализ и построение профиля выполняем следующим образом:
1. Находим минимальную (qmin) и максимальную (qmax) сумму спроса в исследуемом периоде (соответственно 51 и 71 единиц).
2. Задаем определенное число интервалов равной длины внутри интервала (qmin; qmax). Лучше, если число интервалов удовлетворяет условию 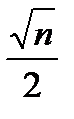 < k <
< k < 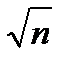 , где n число данных.
, где n число данных.
3. Включаем отдельные значения спроса в исследуемом периоде в соответствующие интервалы и определяем число значений в каждом из интервалов.
4. Представляем полученный ряд распределения графически в виде гистограммы как профиль спроса.
Таблица 4.5. Еженедельный спрос на изделие KL002
| 71 (max) | ||||||||||||
| 51 (min) |
Следуя указанному алгоритму, получаем профиль спроса, представленный на рисунке 4.7.
Рисунок 4.7. Профиль недельного спроса для изделия KL002
Профиль спроса, полученный в соответствии с указанным алгоритмом, является хорошим источником информации о природе спроса на данный материал (товар). Однако трудно себе представить применение такого алгоритма в случае одновременного управления многими тысячами позиций. Кроме того, кроме качественной информации о характере спроса необходима также и количественная, позволяющая рассчитывать уровень обслуживания клиентов и страховой запас.
Отсюда следует необходимость подгонки эмпирического распределения к одному из теоретических. Подберем теоретическое распределение, описывающее характер спроса на изделие, по данным, представленным в таблице 4.6.
Таблица 4.6. Распределение размера спроса на изделие
| Размер спроса (qi) | ||||
| Количество дней (n) |
Как видно из данных таблицы, в течение года продали 67 штук этого изделия. Спрос на это изделие единичный и можно предположить, что вероятность его покупки отдельным покупателем очень мала. В таких случаях, когда много клиентов, но низкая вероятность покупки - очень хорошим приближением эмпирического распределения является распределение Пуассона.
Распределение Пуассона используется для редко продаваемых товаров, когда средний размер спроса (в единицу времени) 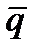 приблизительно равен его среднему стандартному отклонению
приблизительно равен его среднему стандартному отклонению 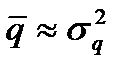 ; вероятность того, что в данный день будет спрос на х единиц изделий равна
; вероятность того, что в данный день будет спрос на х единиц изделий равна 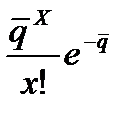 (где е - основание натурального логарифма).
(где е - основание натурального логарифма).
При этом:
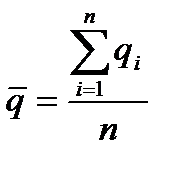 ;
; 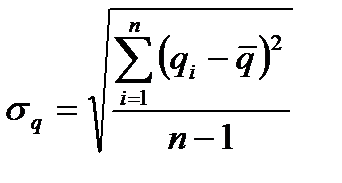
 = 0,215 (при 312 рабочих днях), стандартное отклонение
= 0,215 (при 312 рабочих днях), стандартное отклонение 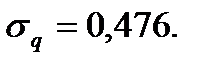 Таким образом,
Таким образом, 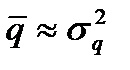 и для описания эмпирического распределения дневного спроса в данном случае подходит распределение Пуассона при среднем дневном спросе
и для описания эмпирического распределения дневного спроса в данном случае подходит распределение Пуассона при среднем дневном спросе 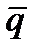 = 0,215. Соответствие принятого теоретического распределения эмпирическому можно определить с помощью одного из статистических тестов. На рисунке 4.8 показаны оба распределения эмпирическое и принятое теоретическое распределение Пуассона. Рисунок подтверждает большое соответствие данных распределений.
= 0,215. Соответствие принятого теоретического распределения эмпирическому можно определить с помощью одного из статистических тестов. На рисунке 4.8 показаны оба распределения эмпирическое и принятое теоретическое распределение Пуассона. Рисунок подтверждает большое соответствие данных распределений.
Рисунок.4.8. Распределение Пуассона, как теоретическое распределение, описывающее спрос на изделие
Подберем теоретическое распределение, описывающее характер спроса на изделие, по данным, представленным в таблице 4.7.
Таблица 4.7. Распределение размера спроса на изделие
| Размер спроса | |||||||||||
| Количество дней |
На данном примере видно, что с увеличением среднего дневного спроса 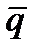 меняется форма профиля спроса. Однако в данном случае
меняется форма профиля спроса. Однако в данном случае 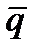 =2,92 а
=2,92 а 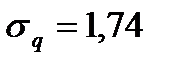 и
и 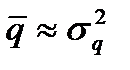 . Поэтому и здесь можно принять распределение Пуассона как приближенное теоретическое. Сравнение эмпирического и теоретического распределений показано на рисунке 4.9.
. Поэтому и здесь можно принять распределение Пуассона как приближенное теоретическое. Сравнение эмпирического и теоретического распределений показано на рисунке 4.9.
Подберем теоретическое распределение, описывающее характер спроса на изделие по данным, представленным в таблице 4.8.
Рисунок 4.9. Распределение Пуассона, как теоретическое распределение, описывающее спрос на изделие
Таблица 4.8. Распределение размера спроса на изделие
| Размер спроса | |||||||||||||||||
| Количество дней |
В этом случае 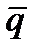 =9,94 а
=9,94 а 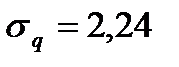 , т.е.
, т.е. 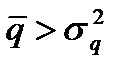 . Попытка применить в данном случае распределение Пуассона неудачна (рисунок 4.10).
. Попытка применить в данном случае распределение Пуассона неудачна (рисунок 4.10).
В условиях, когда спрос на товар значительно варьирует и достаточно велик, для описания характера спроса чаще всего используют нормальное распределение. Оно характеризуется двумя параметрами – средней величиной спроса и его стандартным отклонением. На рисунке 4.11 графически представлено эмпирическое распределение спроса и его нормальное распределение с параметрами 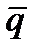 =9,94 а
=9,94 а 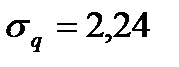 . На рисунке заметно, что нормальное распределение достаточно близко к экспериментальному.
. На рисунке заметно, что нормальное распределение достаточно близко к экспериментальному.
Рисунок 4.11.Нормальное распределение как модель описания характера спроса на изделие
Третье теоретическое распределение, часто применяемое для описания характера спроса на товары, - экспоненциальное распределение. Оно применяется тогда, когда мы имеем дело с совершенно «свободной» продажей (расходом), но при расчете среднего спроса и стандартного отклонения получаем 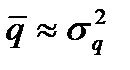 .
.
В таблице 4.9 представлены эмпирические данные дневной потребности на сырье, которое используется в незначительных количествах со значительным его варьированием. Подберем теоретическое распределение, описывающее распределение размера данной потребности.
Таблица 4.9. Распределение размера потребности в материале
| Размер спроса | 0-1 | 1-2 | 2--3 | 3-4 | 4-5 | 5-6 | 6-7 | 7-8 | 8-9 | 9-10 | 10-11 | 11-12 | 12-13 | 13-14 |
| Количество дней |
Средний размер потребности в данном случае 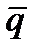 =2,07, а
=2,07, а 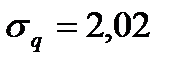 , т. е.
, т. е. 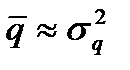 и есть основание применить в данном случае экспоненциальное распределение. Рисунок 4.12 подтверждает хорошее приближение при его использовании.
и есть основание применить в данном случае экспоненциальное распределение. Рисунок 4.12 подтверждает хорошее приближение при его использовании.
Рисунок 4.12. Экспоненциальное распределение как модель описания характера спроса на материал
Анализ тренда и сезонности спроса. Спрос формируется под влиянием многих факторов, одни из которых, будучи основными, определяют закономерность, тенденцию развития, другие – случайные – вызывают колебания уровней. Можно выделить: сезонные изменения, краткосрочный и долгосрочный тренд и случайные отклонения.
Изучая динамику изменения спроса эти составляющие пытаются разделить и выявить основную закономерность его изменения в отдельные периоды, т.е. выявить общую тенденцию в изменении спроса, освобожденную от действия случайных факторов. С этой целью ряды динамики подвергают обработке.
Существует несколько методов обработки рядов динамики, помогающих выявить основную тенденцию изменения уровней ряда. К ним относятся: метод укрупнения интервалов; метод скользящей средней и аналитическое выравнивание.
Во всех методах вместо фактических уровней при обработке ряда рассчитываются иные (расчетные) уровни, в которых тем или иным способом взаимопогашаются действия случайных факторов и тем самым уменьшается колеблемость уровней. Последние в результате становятся как бы «выровненными», «сглаженными» по отношению кисходным фактическим данным. Такие методы обработки рядов называются сглаживанием или выравниванием рядов динамики.
Метод укрупнения интервалов применяют если первоначальные уровни ряда относятся к коротким промежуткам времени. Расчет итогового значения или средней величины исследуемого показателя за укрупненные промежутки времени позволяет более четко выявить закономерность изменения показателя во времени.
При использовании метода скользящей средней фактические уровни заменяют средними уровнями, рассчитанными для последовательно подвижных (скользящих) укрупненных интервалов, охватывающих m уровней ряда.
Например, если принять m=3, то сначала рассчитывается средняя величина из первых трех уровней, затем находится средняя величина из второго, третьего и четвертого уровней, потом из третьего, четвертого и пятого и т.д., т.е. каждый раз в сумме трех уровней появляется один новый уровень, а два остаются прежними. Это обуславливает взаимопогашения случайных колебаний в средних уровнях. Рассчитанные из m членов скользящие средние относятся к середине (центру) каждого рассматриваемого интервала.
Сглаживание методом скользящей средней можно проводить по любому числу членов т, но удобнее, если т – нечетное число, так как. в этом случае скользящая средняя сразу относится к конкретной временной точке – середине (центру) интервала. Если же т – четное,то скользящая средняя относится к промежутку между временными точками.
Тогда, чтобы сглаженные уровни относились непосредственно к конкретным временным точкам (датам), из каждой пары смежных промежуточных значений скользящих средних находят среднюю арифметическую, которую и относят к определенной дате (периоду). Такой прием двойного расчета сглаженных уровней называется центрированием.
Недостатком метода скользящей средней является то, что сглаженный ряд «укорачивается» по сравнению с фактическим с двух концов: при нечетном m на (т – 1)/2 с каждого конца, а при четном – на т/2 скаждого конца.
Этот метод сглаживания, как и укрупнение интервалов, является механическим и не позволяет выразить общую тенденцию изменения уровней в виде математической модели.
Суть метода аналитического выравнивания заключается в замене эмпирических (фактических) уровней, теоретическими, которые рассчитаны по определенному уравнению, принятому за математическую модель тренда, где теоретические уровни рассматриваются как функция времени:
Задача аналитического выравнивания сводится к следующему: определение на основе фактических данных вида (формы) гипотетической функции, способной наиболее адекватно отразить тенденцию развития исследуемого показателя; нахождение по эмпирическим данным параметров указанной функции (уравнения); расчет по найденному уравнению теоретических (выровненных) уровней.
Колебания уровней ряда могут носить разный характер. Наряду с трендом выделяют: циклические (долгопериодические); сезонные (обнаруживаемые в рядах, где данные приведены за кварталы или месяцы); случайные колебания.
В рядах динамики, уровни которых являются месячными или квартальными показателями, наряду со случайными колебаниями часто наблюдаются сезонные колебания, под которыми понимается периодически повторяющееся из года в год повышение и снижение уровней в отдельные месяцы или кварталы.
При изучении рядов динамики, содержащих «сезонную волну», ее выделяют из общей колеблемости уровней и измеряют. Существует ряд методов для решения этой задачи.
Все они основаны на сравнении фактических уровней каждого месяца (или квартала) со средним уровнем, предполагающим равномерное распределение годового показателя по месяцам (или кварталам), либо со сглаженными скользящими средними или выровненными по уравнению тренда.
При этом для измерения «сезонной волны» рассчитывают либо абсолютные разности (отклонения) фактических уровней от среднего уровня (или от выровненных), либо отношения месячных уровней к среднему месячному уровню за год, так называемые индексы сезонности:
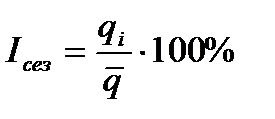
Зная уравнение тренда и средние индексы сезонности, можно продлить ряд, т.е. спрогнозировать квартальные уровни при условии, что выявленная закономерность развития устойчива и сохранится в прогнозируемом периоде (рис. 4.13).
Рисунок 4.13. Прогноз спроса с учетом сезонности
Дата добавления: 2016-02-20; просмотров: 3446;
