Методи прийняття рішень за умов апріорної

Визначеності

2.1. Методи багатокритеріальної оптимізації

Задача багатокритеріальної оптимізації (1.4.2) є некоректною, тому що у загальному випадку не забезпечує визначення єдиного оптимального рішення з допустимої множини X. Цю некоректність можна усунути шляхом регуляризації задачі, тобто введенням деякої додаткової інформації, математичних співвідношень або правил, що дають змогу забезпечити вибір єдиного рішення. При реалізації евристичного підходу джерелом регуляризаційної інформації є особа, що приймає рішення, (ОПР) на інтуїтивному рівні.

Формальний (конструктивний) підхід ґрунтується на визначенні формальних правил вибору єдиного рішення із області компромісів. При цьому можливі два випадки.

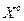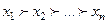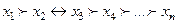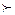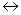1. Рішення ранжирують за порядком спадання чи зростання якості на множині компромісу або, у загальному випадку, на всій допустимій множині X, тобто визначають строгий , або нестрогий порядок, де і є знаками відповідно переваги й еквівалентності. Потім знаходять екстремальний (крайній) елемент ряду.

2. Безпосередньо визначають екстремальне рішення .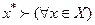

Загальний підхід до розв'язання цієї проблеми полягає в трансформації багатокритеріальної задачі в однокритеріальну зі скалярним критерієм. Існує декілька способів трансформації багатокритеріальних оптимізаційних задач в однокритеріальні. Розглянемо основні з них [12].

Метод головного критеріюбазується на виділенні головного критерію і переведенні всіх інших критеріїв у обмеження. Для цього проводиться аналіз конкретних особливостей багатокритеріальної задачі, із множини частинних критеріїв вибирається один – найважливіший, який береться за єдиний критерій оптимізації. Для кожного з інших частинних критеріїв призначається граничне значення, нижче якого він не може опускатися. Отже, всі частинні критерії, крім одного, перетворюються в обмеження, що додатково звужують множину допустимих рішень X. Тоді вихідна багатокритеріальна задача (1.4.2) перетворюється в однокритеріальну^

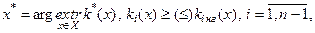(2.1.1)

де k^*(х) - оптимізаційний скалярний критерій; 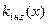– найгірші допустимі значення частинних критеріїв–обмежень; знак " 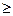" використовується для критеріїв, що потрібно максимізувати, а знак " 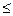" - мінімізувати. Вибір головного (оптимізаційного) критерію і рівнів обмежень 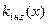для всіх інших критеріїв є суб'єктивною операцією, здійснюваною експертами або ОПР. Слід зазначити, що можна розглянути кілька різних варіантів і порівняти результати.

Реалізуючи розглянутий метод, потрібно звертати особливу увагу на те, щоб допустима множина рішень, яка задана частинними критеріями-обмеженнями, не виявилась порожньою.

Функціонально-вартісний аналіз.Вихідна множина частинних критеріїв К={k_i(x)}, 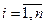, що за визначенням досить повно характеризує ефективність допустимих рішень х 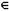X у цілому, розбивається на дві підмножини: К_ф ={k_j,(х)}, 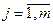і K_B={k_l(x)} , 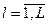; m+L=n. Перша група критеріїв К_ф характеризує функціональну якість рішення, тобто ступінь досягнення цілі системи, що аналізується, а друга група К_В – витрати, потрібні для досягнення цілі. З кожної із зазначених підмножин виділяється один головний критерій; позначимо їх відповідно К^*_ф і К^*_В, а інші частинні критерії переводяться в обмеження. Одержуємо оптимізаційну задачу з двома скалярними критеріями, яку треба звести до однокритеріальної. У функціонально-вартісному аналізі використовуються такі оптимізаційні критерії.

1. Якщо обидва критерії К^*_ф і К^*_В,мають однакову вимірність або їх можна звести до однакової вимірності, то використовується узагальнений оптимізаційний критерій

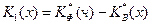(2.1.2)

аоптимальне рішення визначається за схемою

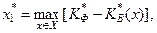(2.1.3)

де X – звужена додатковими обмеженнями область допустимих рішень. Критерій К₁(х) може бути інтерпретований як прибуток системи.

2. Якщо критерії К^*_ф і К^*_В,мають різну вимірність, то використовується критерій

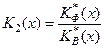, (2.1.4)

а оптимальне рішення має вигляд:

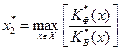. (2.1.5)

Критерій К₂(х)являє собою нормований на одиницю витрат ефект системи.

В окремому випадку для зведення двокритеріальної задачі до однокритеріальної у функціонально-вартісному аналізі використовується принцип головного критерію. Тоді один із двох розглянутих критеріїв К^*_ф або К^*_в перетворюється в додаткове обмеження, і оптимізаційні задачі мають відповідно вигляд:

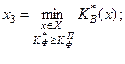(2.1.6)

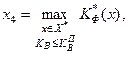(2.1.7)

де К_ф^П , К_В^П – допустимі рівні відповідних критеріїв.

Функціонально-вартісний аналіз застосовується при дослідженні соціально-економічних і технічних систем, які мають однакову якісну залежність ефекту К_ф^* від витрат К_ф^*, що описується логістичною (іноді її називають S-подібною) кривою.

У загальному випадку ця залежність широко використовуєься для аналізу життєвого циклу систем, що починається в момент зародження ідеї (принципу) створення системи і містить у собі етапи реалізації, інтенсивного розвитку, морального старіння і завершується заміною її новою, більш прогресивною системою. При цьому поряд із задачами оцінювання і порівнювання ефективності різних варіантів рішень на всіх етапах (розроблення, створення, модернізація, реінжиніринг) життєвого циклу виникають специфічні задачі стратегічного планування розвитку, тобто визначення моментів і розмірів витрат на нове розроблення, модернізацію існуючих систем, заміну їх новими тощо.

Метод послідовної оптимізації (лексикографічного впорядкування).Ідея цього методу полягає в трансформації багатокритеріальної оптнмізаційної задачі в упорядковану послідовність однокритеріальних. Для цього всі частинні критерії упорядковуються в послідовності спадання важливості, тобто встановлюється лінійний порядок

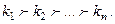(2.1.8)

У цій послідовності розв'язуються однокритеріальні оптимізаційні задачі за кожним частинним критерієм. Метод послідовної оптимізації зводиться до правила впорядкування слів за алфавітом при створенні словників, тому його іноді називають методом лексикографічного упорядкування рішень.

Відповідно до принципу послідовної оптимізації з рішень 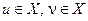перше більш переважно, тобто 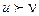, якщо виконуються умови:

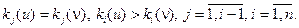(2.1.9)

Звідси найкраще рішення визначається за наступною схемою. На першому кроці з вихідної множини допустимих рішень X виділяється підмножина 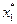рішень, які є еквівалентними (рівноцінними) за першим (найважливішим) критерієм. Для цього розв'язується однокритеріальна оптимізаційна задача:

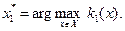(2.1.10)

Якщо множина 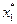містить понад одне рішення, переходимо до наступного етапу, тобто розв'язуємо задачу вибору еквівалентних рішень за другим за важливостю критерієм, але вже з множини :

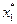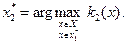(2.1.11)

У загальному випадку

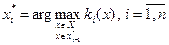
Оптимізація продовжується доти, поки на 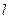-му кроці не дістанемо єдине рішення або не вичерпаються всі критерії. Якщо всі частинні критерії вичерпані, але єдине рішення не отримано, формуються додаткові критерії.

Отримане єдине рішення береться як найкраще (оптимальне). Якщо треба ранжирувати всю множину рішень х 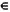X, то отримане найкраще рішення виключається з X, і на множині рішень, що залишилися, повторюється вищеописана процедура. Потім визначаємо друге за якістю рішення і так далі, поки не будуть упорядковані всі рішення.

Коли вже на перших кроках оптимізації знайдено єдине рішення, усі наступні частинні критерії втрачають сенс. Тут може бути застосована схема поступки. Відповідно до цієї схеми ОПР призначає допустимий рівень зниження 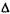k_i(х) частинного критерію, за яким отримано вищезазначене єдине рішення, у порівнянні з екстремальним значенням цього критерію:

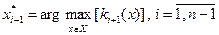(2.1.12)

за умови k_i(х) > 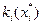– 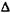k_i(х).

Вибір розміру поступки є евристичною операцією, яка здійснюється ОПР і залежить від особливостей задачі оптимізації. Залежність 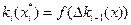має неявний характер і у більшості випадків не є апріорно передбаченою. Тому для вибору значення поступки k_i(x) часто використовуються людино-машинні процедури, коли ОПР призначає деякий ряд значень поступки і, аналізуючи результати оптимізації для кожного з них, приймає рішення про доцільний рівень поступки.

Метод послідовної оптимізації широко застосовується в ситуаціях, коли ОПР має у своєму розпорядженні тільки якісну інформацію про важливість частинних критеріїв.

Метод формування узагальненого скалярного критерію, що враховує всірізнорідні частинні критерії.У цьому випадку єдиний скалярний крите­рій К формується як функціонал частинних критеріїв

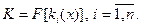(2.1.13)

Це найбільш загальний і універсальний підхід до розв'язання задачі багатокритеріальної оптимізації, відомий як проблема багатофакторного оцінювання.

2.2. Метод дерева рішень [15]

Розглянемо багатокрокову задачу прийняття рішень, що може розглядатися, наприклад, при максимізації прибутку або мінімізації витрат. Нехай одержання прибутку реалізується на кожному кроці процесу прийняття рішень, а потім ці прибутки додаються. Модель такої багатокрокової задачі прийняття рішень може бути подано у вигляді орієнтованого графу, що називається деревом рішень і вказує шлях із заданої множини початкових вершин в задану множину його кінцевих вершин. При цьому з кожною вершиною графа асоціюється деякий стан 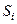, в якому знаходиться об’єкт прийняття рішень, а дуги, що виходять з вершини, відповідають можливим переходам з одного стану в інший залежно від рішень, що приймаються. На рис. 2.2.1 наведено приклад детермінованого дерева рішень. Тут зліва знаходяться заштриховані початкові вершини, а справа – кінцеві вершини. При цьому кожна гілка графу має свою вагу – дійсне число, що враховує витрати на перехід в інший стан. Основна задача полягає в оптимальному виборі початкової вершини із множини допустимих та оптимізації шляху із неї в будь-яку допустиму кінцеву вершину. Задача оптимізації допустимого шляху полягає в мінімізації сумарних витрат і адекватна задачі вибору мінімального шляху в графі. У частковому випадку множини допустимих початкових і кінцевих вершин можуть бути одноелементними.

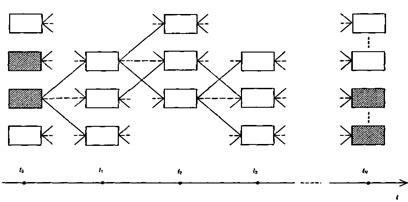
Рисунок 2.2.1 – Дерево рішень за умов визначеності

У наведеному прикладі граф містить тільки так звані основні, або "розв’язуючі" вершини (рис. 2.2.2). При цьому вважається, що система (об’єкт прийняття рішень) знаходиться у визначеному фазовому стані 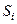, число яких скінчено. Із вершини 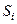виходить декілька дуг графа, кожна з яких відповідає різним рішенням, що можуть прийматися в даному стані. Вибір конкретної альтернативи 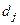призводить до переходу системи в нову розв’язуючу вершину (новий стан).

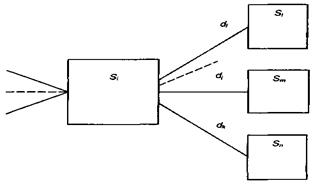
Рисунок 2.2.2 – " Розв’язуючі " вершини

Якщо вибір конкретного рішення 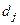визначає не новий стан системи, а задає деяку лотерею на множині можливих нових станів (щільність розподілу ймовірностей), то має місце ймовірнісний зв’язок між вершинами графа (рис. 2.2.3).

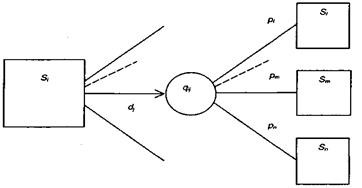
Рисунок 2.2.3 – Імовірнісний зв’язок вершин

У ймовірнісному дереві рішень (рис. 2.2.3) після вибору 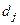ми попадаємо в деяку випадкову допоміжну вершину 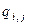і далі переходимо в один із можливих для даного кроку станів 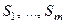у відповідності із заданими ймовірностями 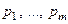, де .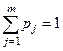

У випадку апріорної невизначеності структура рис. 2.2.3 зберігається, але стрілки, що виходять із вершини 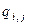вже не будуть мати вагових коефіцієнтів, оскільки відповідні ймовірності відсутні.

2.3. Детермінований метод Беллмана

Розглянемо конкретный приклад детермінованого дерева рішень (рис. 2.3.1) [15].

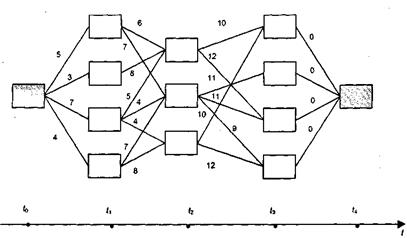
Рисунок 2.3.1– Дерево решень із заданими локальними витратами

На рис. 2.3.1 кінцевими є всі чотирі вершини, що відповідають моменту часу 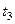. Але шляхом введення фіктивної вершини для 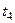вдалося звести задачу до графу з однїєю кінцевою вершиною. Числа у дуг графа означають трудомісткість (витрати), що забезпечують перехід від однієї "розв’язуючої" вершини до іншої. Головна задача полягає у виборі оптимального в сенсі сумарних витрат шляху, який з’єднує початкову та кінцеву вершини.

Основна ідея методу Беллмана складається із двох моментів:

1. Задача пошуку оптимального шляху починає розв’язуватися з кінця.

2. Як початкова вершина послідовно розглядаються всі без винятку вершини графу при одній і тій самій кінцевій вершині.

Реалізуємо метод Беллмана для показаного на рис 2.3.1 графа. Будемо просуватися по графу справа-наліво, відмічаючи в середені кожного квадратика-вершини числа, які дорівнюють найменшим із можливих сумарних витрат при просуванні із поточної початкової вершини по оптимальному шляху, та вказуючи оптимальні напрямки руху з кожної вершини за допомогою стрілок. Наприклад, якщо має місце ситуація, зображена на рис. 2.3.2а, де вершини 2, 3, 4 вже помічено в правому верхнєму куті квадратика, і треба помітити вершину 1, то будемо розмірковувати так. Якщо як початкову взяти вершину 1, то пошук оптимального шляху із неї зводиться до порівняння трьох чисол: 5+10=15, 4+10=14, 4 + 9= 13. Найменше із цих чисол – 13, і тому саме це число записується у вершину 1, а стрілкою з’єднуються вершини 1 и 4 (рис. 2.3.2 б) і відповідно оптимальний маршрут з вершини 1 проходить через вершину 4.

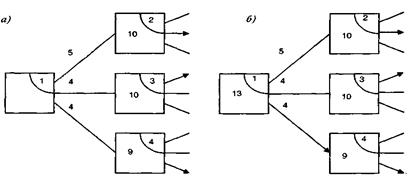
Рисунок 2.3.2 – Метод динамічного програмування Беллмана

Просуваясь справа-наліво і послідовно обробляя вертикальні шари вершин, размічується весь граф (рис. 2.3.3).

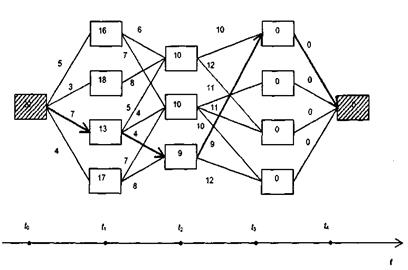
Рисунок 2.3.3 – Розмічений граф

Для відновлення оптимального шляху в графі (2.3.1) тепер достатньо пройти вже зліва-направо у напрямку стрілок, починаючи із вже поміченої початкової вершини (оптимальний шлях на рис. 2.3.3 виділено жирними стрілками). Отримане на етапі розмітки графа число 20 означає мінімальні можливі витрати. Оскільки отимальний шлях може бути не єдиним, то за методом Беллмана одночасно знаходяться всі можливі оптимальні шляхи. При цьому варто розуміти, що глобально оптимальна стратегія не є суперпозицією локально оптимальних стратегій. Наприклад, при спробі побудови оптимального шляху на графі (рис. 2.3.3) при просуванні зліва-направо і виборі кожного разу стрілок з найменшою вагою слід очікувати невдачу, оскільки отримаємо результат: 3+8+10=21, що більше 20.

2.4. Запитання та завдання для самопідготовки

1. Поясніть суть евристичного та формального підходів до розв’язання задачі багатокритеріального прийняття рішень.

2. Яка суть методу головного критерію?

3. Яка суть функціонально-вартісного аналізу?

4. Яка суть методу послідовної оптимізації (лексографічного впорядкування)?

5. Яка основна ідея методу формування узагальненого критерію?

6. Наведіть приклад детермінованого дерева рішень.

7. Що називається “розв’язуючою” вершиною?

8. Наведіть приклад імовірнісного зв’язку між вершинами дерева рішень.

9. Яка основна ідея методу динамічного програмування Беллмана?

10. Знайдіть оптимальний шлях із вершини 1 (рис. 2.4.1):

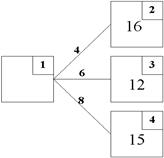k

Рисунок 2.4.1

11. Укажіть оптимальний шлях у наведеному на рис. 2.4.2 графі.

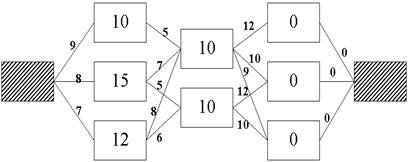
Рисунок 2.4.2