Риск и доход инвестиционного портфеля3
Проведенный выше для одиночного актива анализ достаточно легко обобщить на случай инвестиционного портфеля. Ожидаемый доход Řp инвестиционного портфеля, состоящего из n активов, каждый соответственно c ожидаемым доходом Ři и удельным весом в портфеле wi, можно выразить формулой:
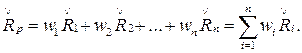(3.7)
При этом необходимо иметь в виду, что удельные веса рассчитываются не от номинальной, а от рыночной стоимости соответствующих инвестиций, и сумма всех весов равна единице.
Определим несколько новых понятий. Под флуктуацией инвестиционного актива, в частности ценной бумаги, будем понимать изменение во времени полного дохода (доходности) на этот актив. Степень совпадения флуктуации двух активов в одном или противоположных направлениях, называется корреляцией. Статистической мерой корреляции является коэффициент корреляции, который будем обозначать ρ либо ρij, где номера i и j относятся к соответствующим активам. Коэффициент корреляции теоретически может лежать в пределах от –1 до + 1. В первом случае мы имеем строго негативную корреляцию, во втором – строго позитивную. Нулевой коэффициент корреляции означает, что доходы на рассматриваемые активы не коррелируют между собой. Соответствующие иллюстрации представлены на рис. 3.1, 3.2, 3.3.
На практике достижение как строго позитивной, так и строго негативной корреляции между инвестиционными активами вряд ли возможно. Примером позитивной корреляции могут служить доходы на акции компаний, работающих в одной отрасли и в одном регионе либо одной стране (последнее необходимо для того, что избежать влияния ряда рисков, включая политические). С известной долей осторожности можно утверждать, что негативно коррелируют между собой доходности обыкновенных акций и облигаций[28].
Рис. 3.1. Строго позитивная корреляция (ρ=1)
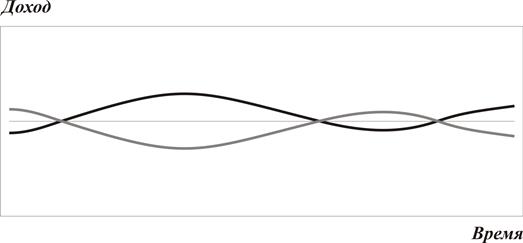
Рис. 3.2. Строго негативная корреляция (ρ=-1)
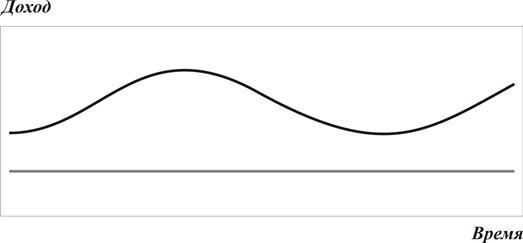
Рис. 3.3. Нулевая корреляция (ρ=0)
Введенный выше коэффициент корреляции тесно связан с другой величиной, используемой для описания того, насколько две величины "ковариируют" друг с другом – ковариацией σij. Обозначая через σi и σj соответственно стандартные отклонения доходности активов с номерами i и j, выражение для ковариации можно представить в виде:
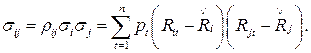(3.8)
Отметим, что равенства (3.8) позволяют выразить коэффициент корреляции через ковариацию и стандартные отклонения. Таким образом, ковариация позволяет учесть не только относительное поведение доходностей двух активов, но и уровень риска, присущий каждому из активов. Последний выражается амплитудой колебаний доходности активов во времени, которая в свою очередь характеризуется стандартными отклонениями σi и σj.
Несложный анализ показывает, что ковариация может принимать как положительные, так и отрицательные значения. Если два актива имеют в целом позитивную корреляцию, то и отклоняться от ожидаемого значения они будут в одном направлении (положительном либо отрицательном), а значит их произведения, стоящие в правой части выражения (3.8), будут положительны. Наоборот, при негативной корреляции эти произведения будут отрицательны, что приведет к отрицательному значению всей суммы. Если изменение доходности обоих активов носит случайный характер, положительные и отрицательные слагаемые в правой части выражения (3.8) будут гасить друг друга, и значение ковариации окажется близким к нулю. Нулевым значение ковариации будет и в случае, когда хотя бы один из активов является безрисковым (см. рис. 3.3).
Дисперсия портфеля
В общем случае дисперсия портфеля, состоящего из n инвестиционных активов, имеет вид:
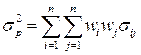(3.9)
В частном случае портфеля, состоящего из двух активов, дисперсия приобретает следующий вид:
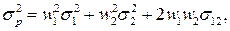или, с учетом формулы (3.8),
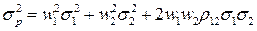(3.10)
В основе современного подхода к финансовому риску лежит предположение о невозможности правильно измерить риск отдельной ценной бумаги в отрыве от других составляющих инвестиционного портфеля[29]. Это положение легко проиллюстрировать, используя введенное понятие дисперсии портфеля как количественную меру риска.
Нашей целью будет показать на примере, как при прочих равных условиях можно добиться снижения риска инвестиционного портфеля, измеряемого его дисперсией, за счет комбинации инвестиционных активов, если корреляция последних не является строго позитивной. Предположим для простоты, что в распоряжении инвестора имеются лишь два инвестиционных актива – актив А и актив В. Для иллюстрации именно портфельного эффекта, предположим, следуя [Levy, Sarnat], что указанные выше активы имеют одинаковые распределения дохода, не имея при этом строго позитивной корреляции. Для определенности предположим, что корреляция между этими активами нулевая (ρАВ = 0). Предположим также, что инвестор может вложить имеющиеся у него средства либо только в актив А, либо только в В, либо 50% в А, 50% в В.
Если инвестор вкладывает все средства только в один актив, то он имеет равные шансы (то есть вероятность каждого исхода равна 0.5) как заработать 40 коп. на один вложенный рубль, так и потерять 20 коп. Это означает, что ожидаемый доход для портфеля, составленного из одного актива (А или В), составит 40•0.5 + (-20)•0.5 = 10 коп. на каждый вложенный рубль. Риск такого портфеля, измеряемый стандартным отклонением, составит [0.5(40 – 10)2 + 0.5(-20 - 10)2]0.5 = 30 коп. на каждый вложенный рубль. Соответственно, дисперсия такого портфеля составит 900 коп2. Если инвестор решит распределить свои вложения поровну между активами А и В, то ожидаемый доход в соответствии с формулой (3.7) составит те же 10 коп.: Řp = wA ŘA + wB ŘB = 0.5•10 + 0.5•10 = 10 коп. При этом дисперсия портфеля, рассчитанная по формуле (3.10) с учетом нулевой корреляции (ρАВ = 0), составит:
σp2 = wА2σА2 + wВ2σВ2 = 0.52302 + 0.52302 = 450 коп2,
а стандартное отклонение будет равно 21.2 коп. Таким образом, риск комбинированного портфеля существенно снизился по сравнению с портфелем, состоящим из одного актива. Этот эффект имеет место даже несмотря на то, что оба актива, использованных для комбинации, имеют идентичные показатели риска и дохода!
Полученный результат может быть достаточно просто проиллюстрирован и с позиций теории вероятностей.
Дата добавления: 2016-02-20; просмотров: 671;