Приложение 1. Обоснование модели дисконтирования дивидендов

Запишем формулу (2.20) для периода 1:

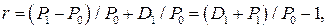(2.23)

откуда текущая оценочная стоимость акции P₀ составит

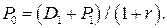(2.24)

С финансовой точки зрения соотношение (2.24) означает, что, оценивая текущую стоимость акции при предполагаемом периоде владения 1 год, инвестор учитывает как дивиденд за этот период, так и прирост ее курсовой стоимости. Вновь применяя формулу (2.20) и принцип дисконтирования, получим оценочную стоимость акции при предполагаемом периоде владения 2 года

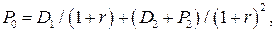(2.25)

где D₂ - ожидаемый дивиденд за год 2, а P₂ - ожидаемая рыночная цена акции на конец второго года. Обратим внимание, что никаких предположений о размере дивидендного выхода, то есть доле прибыли, направляемой на выплату дивидендов, не делается. Даже если вся прибыль реинвестируется, то соотношения (2.24) и (2.25) будут справедливы, просто D₁ и D₂ будут равны нулю, а прирост курсовой стоимости будет демонстрировать значительные темпы9. Последовательно применяя формулу (2.20) и принцип дисконтирования, для бессрочного инвестиционного горизонта получим не что иное, как формулу (2.17). При этом прирост курсовой стоимости в ней нигде не фигурирует, что имеет весьма простое толкование: рано или поздно компания прекратит или замедлит рост и перейдет к выплате дивидендов.