Теорема умножения вероятностей.
Определение. Произведением или пересечением событий A и B называется событие C, состоящее в совместном наступлении этих событий, т. е. в наступлении и события A, и события B.
В случае произведения событий обозначают AВ = С или A∩В = С, или (А и В) = С.
Произведение нескольких событий определяется аналогично.
Дадим определение понятия условной вероятности.
Определение. Вероятность события B при условии, что событие A произошло, называется условной вероятностью события B и обозначается P(B/A) или PA(B).
Аналогично определяется условная вероятность события A, обозначение P(А/В).
Пример 2. В стаде животных из 24 голов одной породы 4 животных не получили прививку. Наудачу последовательно, без возвращения отбирается два животных. Вероятность события A = {первому отобранному животному не сделана прививка}, т. е. P(А) = 4/24= 1/6. Вероятность события В= {второму животному не сделана прививка} при условии, что произошло событие А, Р (В) = 3/23.
Если же первое отобранное животное вернуть в стадо, то P(B) = 4/24=1/6.
В первом случае вероятность события В зависит от того, наступило событие А или нет, а во втором случае не зависит.
Определение. События A и B называются независимыми, если
P(B/A)=P(B) и P(A/B)=P(A)
Если Р(В/А)≠Р(В) или Р(А/В≠Р(А), то события А и В зависимы.
Теорема. Вероятность произведения двух событий, т. е. вероятность совместного наступления событий A и B равна произведению вероятности одного из них на условную вероятность другого.
Доказательство. Пусть для события А благоприятны mА равновозможных элементарных события из общего числа n элементарных исходов, причем mАВ из этих mА событий благоприятны для события В. Тогда по определению (1.5.1) имеем
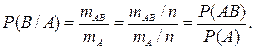
Отсюда следует, что
P(AB)=P(A и B)=P(A)∙P(B/A). (1.6.6)
Теорема доказана.
Если события A и В независимы, то
P(A∙B) = P(A)∙P(B).
Вероятность совместного наступления двух независимых событий равна произведению их вероятностей.
Для вычисления вероятности совместного наступления большего числа событий, например трех, используют формулу
P(A1A2A3)=P(A1)∙P(A2/A1)∙P(A3/A1A2),
где P(А3/А1А2) - вероятность события А3, вычисленная при условии, что события А1 и А2 уже произошли.
Пример 1. Всхожесть семян, предназначенных для посева, оценивается вероятностью в 98%. Вероятность попадания семян в благоприятные для прорастания условия равна 96%. Какой процент семян даст всходы?
Решение. Обозначим А1 - событие = {семенной материал способен дать всходы}, А2 = {семена попали в благоприятные условия}.
Событие С = {посеянные семена дадут всходы} состоит в совместном наступлении событий А1 и А2:
P(C) = P(A1A2) = P(A1)∙P(A2/A1) = 0,98∙0,96 = 0,94.
Таким образом, взойдет 94% семян.
Дата добавления: 2016-02-20; просмотров: 1105;
