П. 1.7. ТЕОРЕМА ПОЛНОЙ ВЕРОЯТНОСТИ. ФОРМУЛА БАЙЕСА
Приведенная ниже формула объединяет теоремы сложения и умножения. Вероятность события A, которое может произойти при условии осуществления одного из несовместных событий В1, В2, В3, ... Bn, образующих полную группу, определяется формулой
(1.7.1)
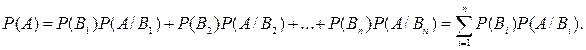
Для наступления события A необходимо и достаточно наступления или события AB1, или события АВ2, или события АВ3, ..., или события ABn,
А=АВ1+АВ2+АВ3+…+АВп
Так как события АВi несовместны, то 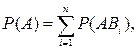 поэтому
поэтому 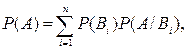 (1.7.2)
(1.7.2)
Пример. Азотное удобрение поступает на склад хозяйства из пункта 1 и пункта 2, причем, из 1-го пункта в 2 раза больше, чем из 2-го. Вероятность события = {удобрение из первого пункта удовлетворяет стандарту}0,9, а соответствующая вероятность для второго пункта равна 0,7.Определить вероятность события А = {взятое для пробы на складе хозяйства удобрение удовлетворяет стандарту}.
Решение. Обозначим
событие В1 = {удобрение поступило из пункта 1};
событие В2 = {удобрение поступило из пункта 2};
Находим
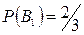 ,
, 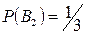 ,
, 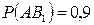 ,
, 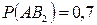 ;
;
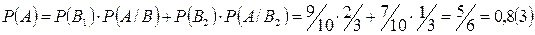
Событие А имеет большую вероятность, оно практически достоверно, т. е. наступит в среднем в 83 случаях из 100.
Формула Байеса. Рассмотрим следующую задачу. На фермах А и В произошла вспышка заболевания ящуром. Доли заражения скота составляют соответственно 1/6 и 1/4. Случайным образом отобранное из одной фермы животное оказалось заболевшим. Найти вероятность события = {животное выбрано из фермы А}. Обозначим:
А = {отобранное животное заражено};
событие В1 = {животное выбрано из фермы А}, Р(B1) = 0,5;
событие В2 = {животное выбрано из фермы В}, Р(B2) = 0,5;
А/В1 = {животное, отобранное из фермы А, заражено};
A/B2 = {животное, отобранное из фермы В, заражено}.
Вероятность события = {животное выбрано из фермы А и заражено} можно записать в виде Р(А)∙Р(В1/А) = P(B1)∙Р(А/В1), откуда
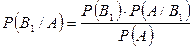 (*)
(*)
или
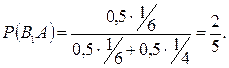
Заменив в (*) Р(А) на 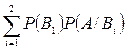 , получим
, получим
· 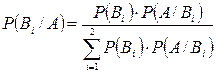 (**)
(**)
Формула (**) является частным случаем формулы Байеса.
Рассмотрим задачу в общем виде. Пусть в результате испытания произошло событие А, которое могло наступить только вместе с каждым из событий B1, В2, В3,..., Вп, образующих полную группу; P(B1), Р(В2), ... , Р(Вп) заранее известны. Требуется найти вероятности событий В1, B2,..., Вп после испытания, когда событие А уже имело место, т. е. P(Bi/A), i=1, 2, ..., п.
Проводя рассуждения, аналогичные приведенным при решении задачи, получим формулу
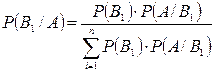 (1.7.3)
(1.7.3)
Эта формула называется формулой Байеса. По формуле (1.7.3) можно вычислить вероятности событий Вi, когда событие А произошло, т. е. переоценить вероятности.
Дата добавления: 2016-02-20; просмотров: 837;
