СХЕМА СРАВНЕНИЯ КОДОВ

Два кода X и Y считаются равными, если попарно равны их одноименные разряды. Можно ввести функцию F(X==Y), которая равна 1, если xi=yi для всех i, иначе ее значение равно нулю. В качестве примера возьмем два двухбитовых числа X=(x1,x0) и Y=(y1,y0).Таблица Карно для этих чисел приведена на рис.31, справа.

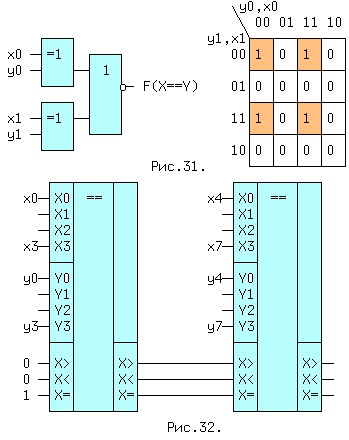
F(X==Y) = ~y1*~x1*~y0*~x0 + ~y1*~x1*y0*x0 + y1*x1*~y0*~x0 + y1*x1*y0*x0 = ~y1*~x1(~y0*~x0 + y0*x0) + y1*x1(~y0*~x0 + y0*x0) = ~(x0 (+) y0)*~(x1 (+) y1) =
F9(x0,y0)*F9(x1,y1) = ~(F6(x0,y0)+F6(x1,y1)). Преобразования в последних двух строчках сделаны с учетом, того что ~F6(x,y) = F9(x,y) и наоборот (см.раздел сумматоры). Одна из
возможных реализаций приведена на рис.31,слева. Практические схемы дополняются функциями "больше/меньше", как например в микросхеме 555СП1, которая сравнивает два четырехразрядных числа. На рис.32 показано соединение двух таких схем, для увеличения разрядности сравниваемых чисел до восьми. Для правильного результата сравнения чисел X = (x7,x6,...,x0) и Y=(y7,y6,...,y0) на вход X = необходимо подать 1. Схема сравнения входит в состав АЛУ микропроцессора и часто называется цифровым компаратором.

2.10 СХЕМА КОНТРОЛЯ ЧЕТНОСТИ (НЕЧЕТНОСТИ)

Схема применяется для выявления одиночных ошибок, вызванных помехами в линии связи или в блоках памяти. Метод основан на подсчете числа единиц в передаваемой в линию или направляемой в память на хранение порции информации, причем если число единиц четное - функция четности P(arity) равна нулю. Для четырехразрядного двоичного числа таблица Карно, схемная реализация и условное обозначение приведены на рис.33.

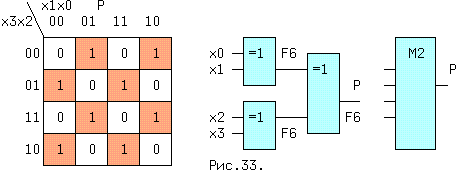
Символом M2 обозначена операция - "сумма по модулю два". Четыре строки таблицы Карно
дают 4 составляющих: P = ~x3*~x2*F6(x1,x0) + ~x3*x2*~F6(x1,x0) + x3*x2*F6(x1,x0) + x3*~x2*~F6(x1,x0) = F6(F6(x3,x2),F6(x1,x0)) = (x3 (+) x2) (+) (x1 (+) x0). Рассмотрим пример на рис.34.

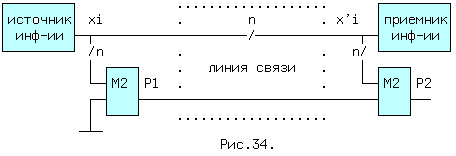
Пусть по n-проводной линии связи передается параллельный двоичный код x(n-1),
x(n-2),...,x1,x0, а принимается код x'(n-1),x'(n-2),..., x'1,x'0. Тогда величина P1 = x0 (+) x1 (+) .. (+) x(n-1) .

На приемном конце линии связи P2 = x'0(+) x'1(+) ... (+) x'(n-1) (+) P1. Подставляя в последнюю формулу выражение для P1 и группируя переменные в одноименные пары, получим: P2 = (x0 (+) x'0) (+) (x1 (+) x'1) (+) (x2 (+) x'2)(+)... Из последнего выражения следует, что если передача прошла без искажений, то xi=x'i и xi (+) x'i =0, а P2=0! При искажении одного и в общем случае нечетного числа бит функция P2=1. Аналогично протекает процесс контроля и при последовательной передаче по одной линии связи n-бит и одного бита четности.