Формализация системы в условиях неопределенности. Нечеткие системы.
Понятие «нечеткая логика» («fuzzy-logic») введена математикой Л.А.Заде (1965 г). Нечеткое множество (НМ) это совокупность элементов, в отношении которых нельзя утверждать определенно: принадлежит ли тот или иной элемент данной совокупности.
При формализации нечеткой системы пользуются экспертной информацией: правилами: если - то.
Центральная роль в теории НС играет лингвистическая переменная  (аналог параметра состояния в обычной математике), которая принимает значение из НМ
(аналог параметра состояния в обычной математике), которая принимает значение из НМ 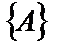 , здесь
, здесь  - нечетное значение,
- нечетное значение, 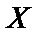 - четное число. Каждой логической переменной
- четное число. Каждой логической переменной  может быть сопоставлена функция принадлежности ФП
может быть сопоставлена функция принадлежности ФП  . Можно выделить 3-и случая выбора «если – то»:
. Можно выделить 3-и случая выбора «если – то»:
1. 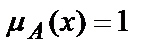 - элемент
- элемент  принадлежит к НМ
принадлежит к НМ 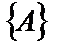 ,
,
2.  - частичная принадлежность к НМ
- частичная принадлежность к НМ 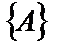 ,
,
3. 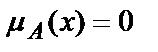 - отсутствие принадлежности к НМ
- отсутствие принадлежности к НМ 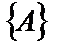 .
.
Относительно НС существуют две противоположные процедуры:
Фаззификация – перевод текущих значений переменной в лонгвистические величины.
Дефаззификация – на основании ФП количественное определение значения выходной лингвистической переменной.
НМ – определяется как множество упорядоченных пар типа  .
.
ФП для различных задач выбираются исходя из субъективных и объективных соображений. Примеры ФП
1. 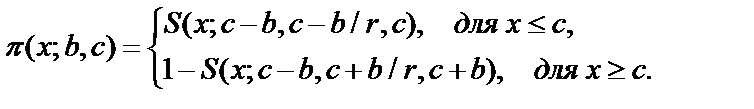 (4.11)
(4.11)
2.  (4.12)
(4.12)
Дата добавления: 2016-02-20; просмотров: 551;
