Основные законы геометрической оптики

ОПТИКА

Геометрическая оптика

Среда отличается от вакуума тем, что она содержит атомы и молекулы вещества. Наличие среды оказывает влияние на распространение света. Следующие параметры среды оказывают влияние на распространение света в ней: показатель преломления, коэффициенты отражения и поглощения, диэлектрическая и магнитная относительные проницаемости среды. Рассмотрим основные законы распространения света в среде.

1. Закон прямолинейного распространения света. В оптически однородной среде свет распространяется прямолинейно.
2. Закон независимости световых пучков. Действие одного пучка не зависит от наличия других пучков.

Рассмотрим падение света на границу раздела двух сред.

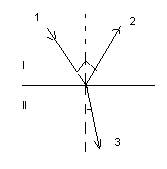
При падении света на границу раздела двух прозрачных сред поведение лучей света подчиняется следующим законам:

1. Закон отражения света. Падающий и отраженный лучи, а также перпендикуляр, восстановленный из точки падения к границе раздела, лежат в одной плоскости. Угол падения, 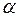, равен углу отражения, .

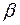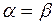. (1)

1. Закон преломления света. Падающий и преломленный лучи, а также перпендикуляр, восстановленный из точки падения к границе раздела, лежат в одной плоскости. Отношение синуса угла падения к синусу угла преломления – есть величина постоянная для данных сред.

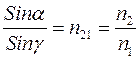(2)

где 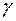- угол преломления, 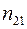- относительный показатель преломления. 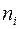- абсолютный показатель преломления 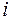-ой среды. Он равен

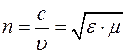(3)

где 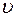- скорость света в среде. 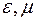- относительные диэлектрическая и магнитная проницаемости среды. Соотношение (2) можно записать в виде

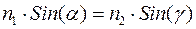(4)

Соотношение (4) симметрично. Из него следует, что световые лучи обратимы.

Если свет распространяется из среды оптически более плотной ( 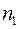) в среду менее плотную ( 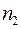): 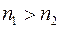, соотношение (2) примет вид:

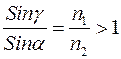(5)

При росте угла 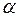угол преломления, 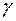, растет до тех пор, пока не станет равным 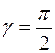. Соответствующий эту значению угол 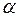называется предельным углом - 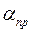. Для углов 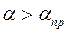весь свет остается в первой среде. Это явление называется полным отражением. В этом случае для 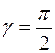из (5) получаем:

.

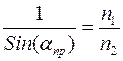
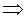
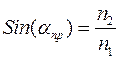Тонкая линза

Световой луч – направление переноса энергии. Он перпендикулярен волновой поверхности.

Линза – оптический прибор, состоящий из прозрачной среды, ограниченной поверхностями. Линзы бывают собирающими и рассеивающими. Линза называется тонкой, если её толщина значительно меньше радиуса кривизны ограничивающих поверхностей. Оптическая ось – прямая, проходящая через центры кривизны поверхностей линзы. Оптический центр линзы – точка, при переходе через которую луч света не преломляется. Будем считать, что оптический центр совпадает с геометрическим центром линзы. Для вывода формулы линзы используется принцип Ферма или принцип наименьшего действия: Свет распространяется по траектории, для прохождения которой требуется минимальное время. Выпишем формулу тонкой линзы без выводов.

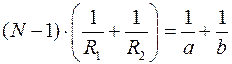(1)

Где 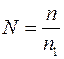; 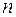- абсолютный показатель линзы; 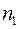- абсолютный показатель среды. 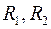- радиусы кривизны первой и второй поверхностей линзы. 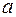- расстояние от центра линзы до точек источника (объекта). 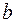- расстояние от центра линзы до точек приемника (изображение).

Формула (1) пригодна для параксиальных лучей. Это лучи, которые образуют малые углы с оптической осью линзы. Радиус кривизны выпуклой поверхности линзы считается положительным, вогнутой поверхности – отрицательным.

Если 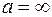, т.е. падающие лучи параллельны оптической оси, то Ур. (1)

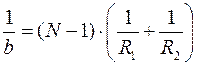
В этом случае 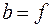- называется фокусным расстоянием линзы.

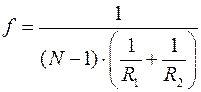
Если 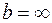, то изображение находится на бесконечности, тогда 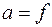. Точки 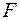, лежащие на расстоянии 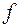равном фокусному, называются фокусами линзы. Фокус – это точка, в которой собираются все лучи, падающие на линзу параллельно оптической оси. Величина

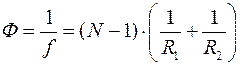(2)

называется оптической силой линзы. Единица измерения 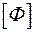- диоптрия (дптр). Это оптическая сила линзы с фокусным расстоянием равным 1м. 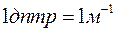. Для собирающей линзы оптическая сила 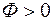, для рассеивающей линзы - 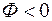. Плоскости, проходящие через фокусы перпендикулярно главной оптической оси, называются фокальными. С учетом определения фокусного расстояния, формула тонкой линзы примет вид:

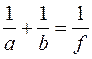(3)

Отношение линейных размеров изображения и объекта называется линейным увеличением линзы.

Построение изображений.

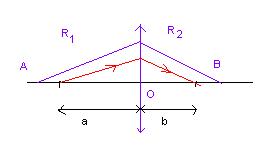
Для построения изображений с использованием тонкой линзы применяются три замечательных луча. Они представлены на рисунке.

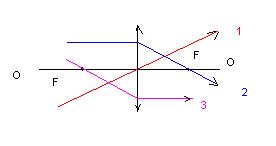
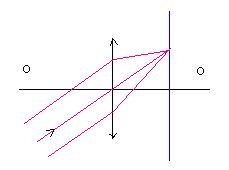
Ось ОО – оптическая ось. Луч 1 проходит через оптический центр линзы без изменения. Луч 2 идет параллельно оптической оси и после прохождения линзы он идет через фокус. Луч 3 проходит через фокус линзы, а после линзы он идет параллельно оптической оси. Кроме того, если на тонкую линзу под углом к её плоскости падает параллельный пучок, то он пересечет фокальную плоскость в одной точке.

Волновая оптика

Световые волны. Монохроматичность. Интерференция света.

Свет – это электромагнитные волны (ЭМВ). ЭМВ не заполняют все пространство. Атомы и молекулы испускают и поглощают волны порциями. Поэтому световая волна ограничена во времени и пространстве. Вводится понятие монохроматической волны – это неограниченная в пространстве волна одной постоянной частоты. Т.О. ЭМВ не являются строго монохроматическими волнами. Время испускания 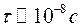. За это время волна проходит расстояние 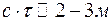. Эта волна называется фотон. Поскольку фотон ограничен в пространстве, его невозможно представить в виде монохроматической волны. Это набор (суперпозиция) волн, имеющие разные частоты. Совокупность таких волн образует волной цуг. В цуге можно выделить колебания с основной частотой. Эту волну можно приближенно рассматривать как монохроматическую в пределах пространства, занимаемого цугом в данный момент времени. Это приближение накладывает определенные ограничения на сложение колебаний. Рассмотрим две световые волны частоты 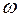. 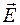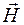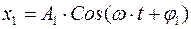В определенной точке пространства это соответствует колебаниям или .

и .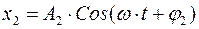

Амплитуда результирующего колебания

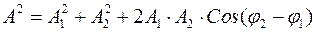
Интенсивность волны пропорциональна амплитуде в квадрате 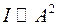, тогда

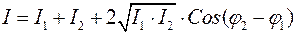(1)

Рассмотрим случай, когда разность фаз 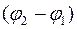постоянная. Эта ситуация соответствует когерентности двух волн (или согласованному во времени и пространстве протеканию двух и более волновых процессов). В зависимости от разности фаз будем иметь разные результаты от сложения двух волн.

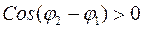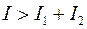, ; и , ;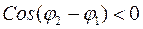

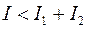Т.о. при наложении двух когерентных световых волн происходит пространственное перераспределение светового потока. В результате возникает чередование максимумов и минимумов интенсивности. Это явление называется интерференцией света. Чтобы наблюдать это явление необходимо иметь две когерентные световые волны. Для этого применяют следующий прием: исходящую волну разделяют на две, каждая из которых проходит свой путь до точки встречи. Причем каждая волна может двигаться в своей среде и проходит своё расстояние. Пусть первый луч прошел путь 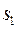в среде с показателем преломления 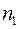, второй луч прошел путь 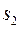в среде с показателем преломления 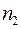. Если в исходной точке 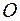, где волна разделяется, фаза колебаний равна 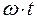, то в точке встречи, 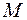, первая волна удовлетворяет уравнению

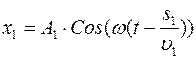. Вторая волна .

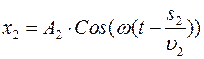Скорость ЭМВ в среде определяется 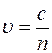. Разность фаз колебаний в точке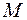

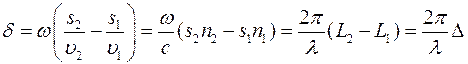
где 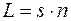оптическая длина пути. 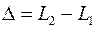- разность оптических длин путей, проходимых волнами– оптическая разность хода лучей. Если

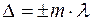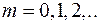и , то ,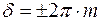

следовательно, волны приходят в одной фазе, наблюдается максимум. Если

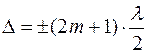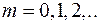и , то ,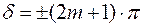

следовательно, волны приходят в противофазе, наблюдается минимум.