Токи при размыкании и замыкании цепи.

Рассмотрим процессы замыкания и размыкания цепи. В этом случае изменяется сила тока и величина магнитного потока. В цепи возникает ЭДС самоиндукции - .

Рис.

Для цепи, изображенной на рисунке, получаем

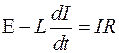. (1)

А) Рассмотрим вначале процесс размыкания цепи. Пусть в момент времени 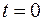цепь разомкнули, что соответствует . Ур (1) примет вид

или . Обозначим .

Дифференциальное уравнение примет вид

. Решение , где 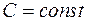. Окончательно

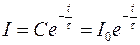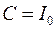, где и 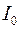- ток в момент времени .

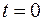Б) процесс замыкания цепи. В момент времени 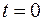имеем . Будем считать, что при 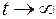имеем установившийся процесс: и 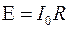. Учитывая установившуюся связь между ЭДС и током из Ур. (1) получаем

далее . Введем новую переменную: 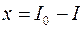Её дифференциал . В новых обозначениях получаем дифференциальное уравнение 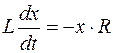. Методом разделения переменных решаем уравнение

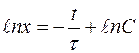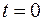. Отсюда определяем . Определяем постоянную интегрирования через . Для этого полагаем и находим . Учитывая, что находим 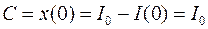. Окончательно

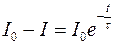и

. Это уравнение описывает процесс установления стационарного состояния в цепи при её замыкании.