Вынужденные колебания при действии периодической возмущающей силы.

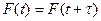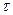Пусть вынуждающая сила зависит от времени (см. рис. 1.14а-в) и изменяется по негармоническому закону, но является периодической функцией, удовлетворяющей условиям Дирихле. Эти условия формулируются так: на конечном интервале функция ограничена, имеет разрывы только первого рода и конечное число экстремумов. В этом случае, во-первых, справедливо равенство , где - период возмущающей силы, во-вторых, функция 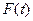допускает разложение в тригонометрический ряд Фурье:

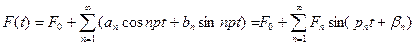, (1.23)

где ; ; ;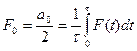

; ; .

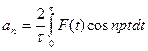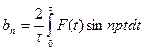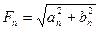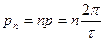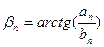Члены ряда Фурье называются гармониками соответствующего порядка (первого, второго, и так далее).

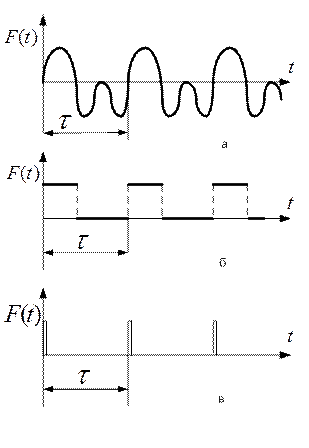
Рис.1.14

Очевидно, что и в этом случае, в силу линейности уравнения движения, решение может быть получено в виде суммы решений, каждое из которых найдено в предположении, что действует только одна гармоника вынуждающей силы, т.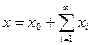е. , где 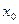- смещение центра установившихся колебаний по отношению к положению равновесия.

На практике число гармоник 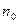должно быть ограничено. Так, если ряд Фурье для функции 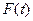сходиться достаточно быстро ( 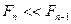, при условии, что 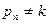- т.е. резонанс отсутствует), то число учитываемых слагаемых определяется желаемой точностью расчета.

Если ряд Фурье сходится медленно, то при ограничении числа гармоник следует руководствоваться следующим соображением: рассмотренная колебательная модель ведет себя как фильтр, пропускающий практически без искажения гармоники с частотами 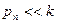, усиливающий гармоники с частотами, близкими к резонансной, и не пропускающий гармоники с частотами 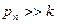(см. амплитудно-частотные характеристики рис.1.9 и 1.13). Тогда, если 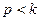, одно (или несколько) кратных значений 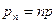могут оказаться в околорезонансной области и, как следствие, вклад соответствующих гармоник в решение будет определяющим; в этом случае число учитываемых гармоник 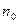должно быть больше числа 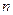, соответствующего резонансному режиму. Если 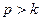, резонанс невозможен, а коэффициент динамичности монотонно убывает; в таком случае можно ограничиться достаточно малым числом учитываемых гармоник.

ПРИМЕР 5. На тело, прикрепленное к пружине [8], действует возмущающая сила, изменяющаяся во времени по закону, изображенному на рисунке 1.15.а. Возмущающая сила 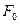действует одну треть периода 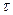. Определить установившиеся вынужденные колебания для двух случаев: 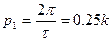и 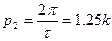, если движение происходит в линейно-вязкой среде ( 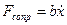) с безразмерным коэффициентом сопротивления .

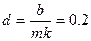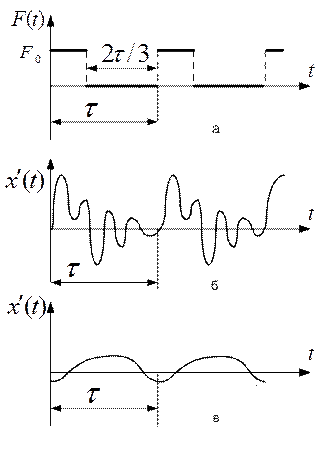
Рис.1.15

Примем за начало отсчета координаты 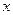положение статического равновесия. Пусть 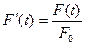- безразмерная возмущающая сила. Представим ее, согласно (1.23), в виде ряда

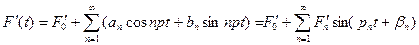
где ; ; ; ; ; .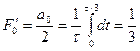

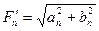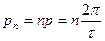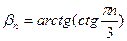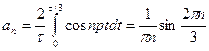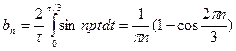Очевидно, что для всех гармоник с порядком 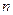, кратным трем, 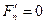, а 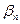не имеет смысла.

Результаты расчета для первых десяти гармоник приведены в таблице 1.1.

Таблица 1.1.