Обработка экспериментальных данных методом дисперсионного анализа
Дисперсионный анализ – это метод, позволяющий определить степень влияния одного или нескольких случайных факторов на протекание исследуемого процесса.
Вначале проводят серии идентичных опытов по измерению величины 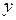 с разными значениями оцениваемого фактора.
с разными значениями оцениваемого фактора.
Определяют математическое ожидание 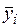 для каждой
для каждой 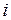 -й серии опытов и математическое ожидание
-й серии опытов и математическое ожидание 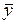 по всем опытам:
по всем опытам:
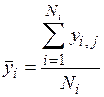 ; (3.1)
; (3.1)
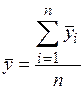 , (3.2)
, (3.2)
где:  - номер измерения;
- номер измерения; 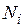 - количество измерений в
- количество измерений в 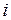 -м опыте;
-м опыте; 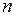 - количество опытов.
- количество опытов.
После этого рассчитывают оценку дисперсии между сериями опытов 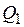 и оценку дисперсии внутри серий опытов
и оценку дисперсии внутри серий опытов 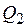 :
:
 ; (3.3)
; (3.3)
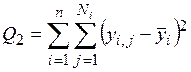 . (3.4)
. (3.4)
Затем рассчитывают параметр критерия Фишера:
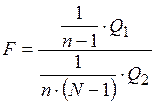 . (3.5)
. (3.5)
Далее определяют степени свободы 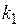 для параметра
для параметра 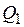 и
и 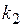 для параметра
для параметра 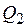 :
:
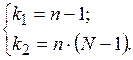 (3.6)
(3.6)
По таблице распределения Фишера (табл. 3.1) и значений 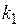 и
и 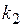 находят параметр
находят параметр 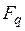 .
.
После этого сравнивают значения 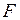 и
и 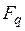 . Если
. Если 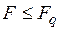 , то влияние рассматриваемого фактора на результаты измерения несущественно. В противном случае влияние этого фактора существенно.
, то влияние рассматриваемого фактора на результаты измерения несущественно. В противном случае влияние этого фактора существенно.
Таблица 3.1
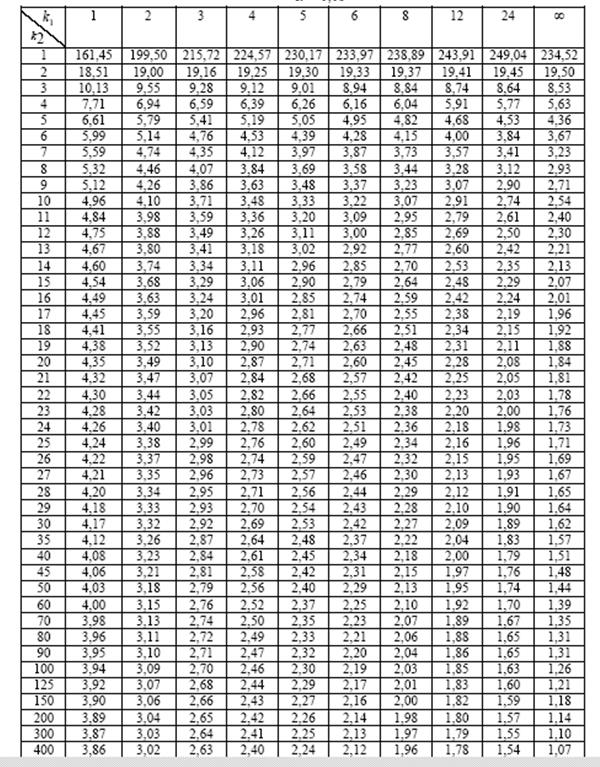
Значения F-критерия Фишера при уровне значимости 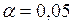
Задача 1
Оценить влияние температуры окружающей среды на результаты измерения одного и того же напряжения с помощью имеющегося вольтметра некоторого типа.
Результаты измерений приведены в табл. 3.2.
Таблица 3.2.
Результаты измерений напряжения, В
| Опыт №1: температура окружающей среды от 15ºС до 18ºС | |||||||
| 220,1 | 220,1 | 220,2 | 220,2 | 220,2 | 220,3 | 220,3 | 220,3 |
| Опыт №2: температура окружающей среды от 18ºС до 21ºС | |||||||
| 220,3 | 220,3 | 220,3 | 220,3 | 220,2 | 220,2 | 220,2 | 220,2 |
| Опыт №3: температура окружающей среды от 21ºС до 25ºС | |||||||
| 220,2 | 220,1 | 220,1 | 220,0 | 220,0 | 220,0 | 220,0 | 220,0 |
Решение
Значения температуры окружающей среды для рассматриваемой задачи не важны. Важен только диапазон этой температуры и его влияние на результаты измерений.
Исходные данные по условию: 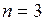 ;
; 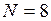 .
.
Определяем математические ожидания измеренных напряжений по опытам в соответствии с (3.1):
 В;
В; 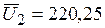 В;
В; 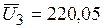 В.
В.
Общее математическое ожидание по (3.2): 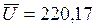 В.
В.
Оценки дисперсий по (3.3) и (3.4): 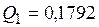
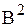 ;
; 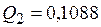
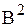 .
.
Параметр критерия Фишера по (3.5): 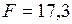 .
.
Степени свободы:  ;
; 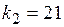 .
.
Параметр критерия Фишера по табл. 3.1:  .
.
Ответ: 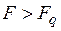 , поэтому влияние температуры на результаты измерений существенно.
, поэтому влияние температуры на результаты измерений существенно.
Задача 2
Оценить влияние оператора на результаты измерений тока с помощью одного и того же стрелочного амперметра.
Результаты опытов приведены в табл. 3.3.
Таблица 3.3.
Результаты измерений тока, А (N – номер по журналу)
| Оператор №1 | |||||||
| N+0,1 | 2N-0,2 | 3N-0,3 | 4N+0,5 | 5N-0,2 | 6N+0,2 | 7N-0,2 | 8N-0,8 |
| Оператор №2 | |||||||
| N+0,2 | 2N-0,3 | 3N | 4N+0,8 | 5N+0,1 | 6N-0,5 | 7N | 8N-0,4 |
| Оператор №3 | |||||||
| N | 2N+0,1 | 3N-0,5 | 4N-0,2 | 5N-0,1 | 6N+0,5 | 7N-0,2 | 8N+0,1 |
| Оператор №4 | |||||||
| N-0,1 | 2N-0,3 | 3N+0,1 | 4N+0,2 | 5N | 6N+0,2 | 7N-0,4 | 8N-0,5 |
Задача 3
Разработайте схему и методику проведения эксперимента для оценки влияния требуемого фактора (табл. 3.4) на точность показаний трёхфазного электронного счётчика активной электроэнергии по методу дисперсионного анализа. Дайте подробное описание принципа работы схемы и методики эксперимента. Приведите примеры таблиц для проведения соответствующих измерений.
Таблица 3.4.
Варианты заданий к задаче №3
| Вариант | ||||
| Влияющий фактор | Высшие гармоники напряжения сети | Высшие гармоники тока нагрузки | Коэффициент мощности нагрузки | Несимметрия трёхфазной системы напряжений |
| <== предыдущая лекция | | | следующая лекция ==> |
| в статике с помощью полного факторного эксперимента | | | Выбор обуви и уход за ней |
Дата добавления: 2016-02-16; просмотров: 904;
