Синхронные параллельные и последовательные НС с дискретными и непрерывными состояниями и временем

Рассмотрим НС с парным взаимодействием [5]. Действие нейрона самого на себя будем считать отсутствующим. Фрагмент такой НС показан на рис. 17.1.

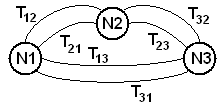
Рис.17.1. Фрагмент НС с парным взаимодействием

В начальный момент сеть характеризуется вектором начальных состояний: 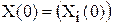. Процесс дальнейшего изменения состояний нейронов определяется следующим уравнением:

,

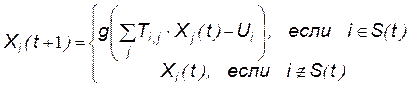где 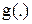- активационная функция, 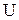- вектор потенциала активации.

Динамические свойства НС определяют одним из следующих правил:

o Синхронная динамика – каждый момент времени активны все нейроны: .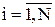

o Параллельная динамика – множество активных нейронов зависит от времени и определяется специальной функцией: .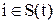

o Последовательная динамика – нейроны работают по одному; номер активного нейрона определяется по некоторому правилу, например случайно или в зависимости от величины выходных сигналов в текущий момент времени.

Состояния НС дискретны или непрерывны, если дискретна или непрерывна активационная функция.

НС с симметричными связями 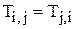, дискретными состояниями и синхронной динамикой может иметь группы зацикленных нейронов; длина зацикливания ограничена числом состояний нейрона. Последовательная динамика исключает зацикливания состояний нейронов. Параллельная динамика в общем случае уменьшает количество зацикленных нейронов, но полностью их исключить не способна.

НС с непрерывными состояниями в зависимости от вида динамики и крутизны активационной функции может иметь следующие виды предельных состояний: стационарное состояние, периодический режим, квазипериодический режим и хаотический режим.

Модель НС с непрерывным временем задают с помощью следующих уравнений:

, ,

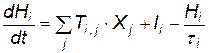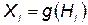где 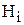- линейный выход нейрона, 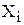- нелинейный выход, 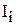- внешний сигнал, 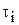- инерционность нейрона. Предельные состояния такой НС всегда стационарны.