Матричная форма МОРО

Наиболее просто метод обратного распространения ошибки представляется в матричной форме. Прямое распространение сигнала по НС, состоящей из N слоев, описывается следующей системой уравнений:

, , …,

, , …,

, .

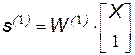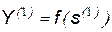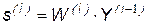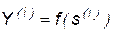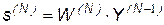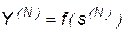Вектор входного сигнала наращивается единичной компонентой, так как необходимо учитывать величину смещения в каждом слое нейронов. Обратное распространение сигнала ошибки по НС позволяет вычислить корректирующие коэффициенты с помощью следующих уравнений:

, …,

,…,

.

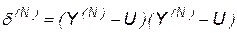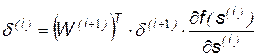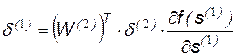Коррекция весовых коэффициентов НС проводится с помощью следующих уравнений:

,…, ,

,…, ,

, .

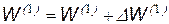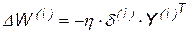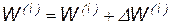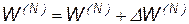где 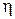– коэффициент скорости обучения.

Приведенные выше уравнения являются компактной формой описания метода обратного распространения ошибки, используемого для обучения нейронных сетей. Применение данных уравнений позволяет строить модели НС с произвольным числом слоев.

Пример зависимости невязки от величины весовых коэффициентов приведен на рис.19.1. Алгоритм построения графиков: трехслойная НС была обучена распознаванию заданных образов, произвольным образом во втором и третьем слоях выбраны два весовых коэффициента, в квадратной окрестности, окружающей оптимальные значения коэффициентов, задана сеть значений коэффициентов, для которых вычислена невязка.

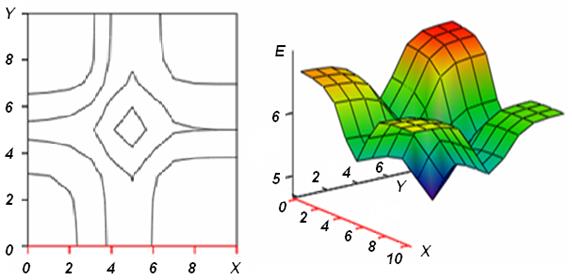
Рис.19.1. Графики зависимости невязки на выходе НС

от значений двух весовых коэффициентов

Приведенные графики наглядно показывают наличие минимума невязки и демонстрируют сложность исследуемой поверхности: к точке минимума сходится 4 взаимно ортогональных канала.