Метод обратного распространения ошибки
Обучение нейронной сети методом градиентного поиска, с учетом слоистой структуры, называется методом обратного распространения ошибки (МОРО – back propagation algorithm)). Данный метод хорошо изучен и достаточно устойчив [2,14,18]. Сигналы ошибки распространяются от выходов НС к ее входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Согласно методу наименьших квадратов минимизируемой целевой функцией ошибки НС является сигнал ошибки обучения:
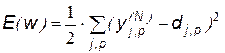 , (18.1)
, (18.1)
где 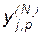 - реальное выходное состояние нейрона j выходного слоя N нейронной сети при подаче на ее входы p-го образа;
- реальное выходное состояние нейрона j выходного слоя N нейронной сети при подаче на ее входы p-го образа; 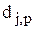 - идеальное (желаемое) выходное состояние этого нейрона. Суммирование ведется по всем нейронам выходного слоя и по всем обрабатываемым сетью образам. Минимизация ведется методом градиентного спуска, что означает подстройку весовых коэффициентов следующим образом:
- идеальное (желаемое) выходное состояние этого нейрона. Суммирование ведется по всем нейронам выходного слоя и по всем обрабатываемым сетью образам. Минимизация ведется методом градиентного спуска, что означает подстройку весовых коэффициентов следующим образом:
 ,
,
где 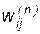 - весовой коэффициент синаптической связи;
- весовой коэффициент синаптической связи; 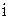 - номер нейрона;
- номер нейрона;  - номер входа нейрона;
- номер входа нейрона; 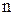 - номер слоя;
- номер слоя;  - коэффициент скорости обучения,
- коэффициент скорости обучения, 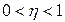 . Производная сложной функции имеет вид:
. Производная сложной функции имеет вид:
 ,
,
где 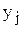 - выход нейрона
- выход нейрона  ;
;  - взвешенная сумма входных сигналов, то есть аргумент активационной функции. Для производной сигнала ошибки по выходному сигналу имеем:
- взвешенная сумма входных сигналов, то есть аргумент активационной функции. Для производной сигнала ошибки по выходному сигналу имеем:
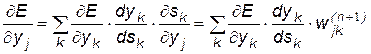 .
.
Здесь суммирование по  выполняется среди нейронов слоя
выполняется среди нейронов слоя 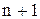 .
.
Введя новую переменную
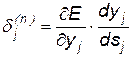 ,
,
получим рекурсивную формулу для расчетов величин 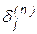 слоя
слоя 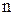 из величин
из величин  слоя
слоя  :
:
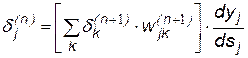 .
.
Для выходного слоя:
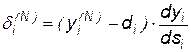 .
.
Теперь можно записать основное выражение для весовых коэффициентов в обобщенном виде:

Рассмотренный метод обучения не всегда приводит к правильному решению, что обусловлено рядом причин. Во-первых, в процессе обучения может возникнуть ситуация, когда большие положительные или отрицательные значения весовых коэффициентов сместят рабочую точку на сигмоидах многих нейронов в область насыщения. Малые величины производной от активационной функции приведут к остановке обучения, что парализует НС. Во-вторых, применение метода градиентного спуска не гарантирует, что будет найден глобальный, а не локальный минимум целевой функции. Эта проблема связана еще с одной, а именно - с выбором величины скорости обучения. Занижение скорости обучения приводит к увеличению длительности обучения. С другой стороны, слишком большие коррекции весов могут привести к потере устойчивости процесса обучения. Несмотря на указанные недостатки, рассмотренный метод считается одним из наиболее эффективных методов обучения нейронных сетей.
Дата добавления: 2016-02-16; просмотров: 843;
