Пример вычисления дисперсии
| № п/п | Значение показателя | Отклонение от среднего | Квадрат отклонения |
| 2 – 1 = +1 2 – 3 = –1 2 – 3 = – 1 2 – 0 = +2 2 – 4 = –2 2 – 1 = +1 | |||
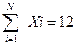
| 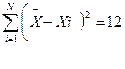
| ||
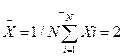
| 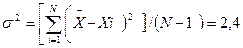
|
Среднее квадратичное отклонение подтверждает типичность и показательность средней арифметической, отражает меру колебания численных значений признаков, из которых выводится средняя величина. Оно равно корню квадратному из дисперсии и определяется по формуле:
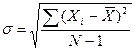 ; (2)
; (2)
где: s – средняя квадратическая. При малом числе наблюдения (действий) – менее 100 – в значении формулы следует ставить не “N”, а “N – 1”.
Средняя арифметическая и средняя квадратическая являются основными характеристиками полученных результатов в ходе исследования. Они позволяют обобщить данные, сравнить их, установить преимущества одной психолого-педагогической системы (программы) над другой.
Среднее квадратическое (стандартное) отклонение широко применяется как мера разброса для различных характеристик.
Оценивая результаты исследования важно определить рассеивание случайной величины около среднего значения. Это рассеивание описывается с помощью закона Гауса (закона нормального распределения вероятности случайной величины). Суть закона заключается в том, что при измерении некоторого признака в данной совокупности элементов всегда имеют место отклонения в обе стороны от нормы вследствие множества неконтролируемых причин, при этом, чем больше отклонения, тем реже они встречаются.
При дальнейшей обработке данных могут быть выявлены: коэффициент вариации (устойчивости) исследуемого явления, представляющий собой процентное отношение среднеквадратического отклонения к средней арифметической; мера косости, показывающая, в какую сторону направлено преимущественное число отклонений; мера крутости, которая показывает степень скопления значений случайной величины около среднего и др. Все эти статистические данные помогают более полно выявить признаки изучаемых явлений.
Меры связи между переменными.Связи (зависимости) между двумя и более переменными в статистике называют корреляцией. Она оценивается с помощью значения коэффициента корреляции, который является мерой степени и величины этой связи.
Коэффициентов корреляции много. Рассмотрим лишь часть из них, которые учитывают наличие линейной связи между переменными. Их выбор зависит от шкал измерения переменных, зависимость между которыми необходимо оценить. Наиболее часто в психологии и педагогике применяются коэффициенты Пирсона и Спирмена.
Рассмотрим вычисление значений коэффициентов корреляции на конкретных примерах.
Пример 1. Пусть две сравниваемые переменные X (семейное положение) и Y (исключение из университета) измеряются в дихотомической шкале (частный случай шкалы наименований). Для определения связи используем коэффициент Пирсона.
В тех случаях, когда нет необходимости подсчитывать частоту появления различных значений переменных X и Y, удобно проводить вычисления коэффициента корреляции с помощью таблицы сопряженности (см. табл. 6.2, 6.3, 6.4)1, показывающей количество совместных появлений пар значений по двум переменным (признакам). А – количество случаев, когда переменная X имеет значение равное нулю, и, одновременно переменная Y имеет значение равное единице; В – количество случаев, когда переменные X и Y имеют одновременно значения, равные единице; С – количество случаев, когда переменные X и Y имеют одновременно значения равные нулю; D – количество случаев, когда переменная X имеет значение, равное единице, и, одновременно, переменная Y имеет значение, равное нулю.
Таблица 6.2
Общая таблица сопряженности
| Признак X | Всего | |||
| Признак Y | А С | В D | A + B C + D | |
| Итого | A + C | B + D | N | |
В общем виде формула коэффициента корреляции Пирсона для дихотомических данных имеет вид
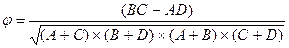 ; (3)
; (3)
Таблица 6.3
Дата добавления: 2015-12-01; просмотров: 1029;
