Пример данных в дихотомической шкале
| Шифр испытуемого | Переменная X | Переменная Y |
Таблица 6.4
Таблица сопряженности для данных из таблицы 6.3
| Признак X | Всего | |||
| Признак Y | ||||
| Итого | ||||
Подставим в формулу данные из таблицы сопряженности (см. табл. 6.4), соответствующей рассматриваемому примеру:
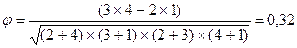 .
.
Таким образом, коэффициент корреляции Пирсона для выбранного примера равен 0,32, то есть зависимость между семейным положением студентов и фактами исключения из университета незначительная.
Пример 2. Если обе переменные измеряются в шкалах порядка, то в качестве меры связи используется коэффициент ранговой корреляции Спирмена (Rs). Он вычисляется по формуле
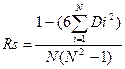 ; (4)
; (4)
где Rs – коэффициент ранговой корреляции Спирмена; Di – разность рангов сравниваемых объектов; N – количество сравниваемых объектов.
Значение коэффициента Спирмена изменяется в пределах от –1 да + 1. В первом случае между анализируемыми переменными существует однозначная, но противоположено направленная связь (с увеличением значений одной уменьшается значения другой). Во втором – с ростом значений одной переменной пропорционально возрастает значение второй переменной. Если величина Rs равна нулю или имеет значение, близкое к нему, то значимая связь между переменными отсутствует.
В качестве примера вычисления коэффициента Спирмена используем данные из таблицы 6.5.1
Таблица 6.5
Данные и промежуточные результаты вычисления значения коэффициента
Дата добавления: 2015-12-01; просмотров: 1212;
