Структура доказательства. В составе доказательства и, конечно, опровержения, поскольку речь идет о доказательстве в широком смысле
В составе доказательства и, конечно, опровержения, поскольку речь идет о доказательстве в широком смысле, выделяются следующие элементы.
1. Тезис доказательства – высказывание, истинность или ложность которого доказывается.
2. Аргументы – высказывания, посредством которых осуществляется доказательство тезиса.
В правильном доказательстве аргументы – это высказывания, истинность которых не вызывает сомнения, и при этом уверенность в их истинности имеет какие-то рациональные основания. Иначе говоря, аргументы – это такие высказывания, которые выражают знание человека о наличии или отсутствии соответствующих – утверждаемых
или отрицаемых в этих высказываниях – ситуаций. Однако следует отметить, что у различных людей может быть различное отношение к одним и тем же высказываниям: для одних – истинность высказываний очевидна, а у других может вызывать сомнения – это обусловливает необходимость учитывать при осуществлении доказательства и вообще в процессе аргументациихарактер аудитории, для которой она предназначена. Таким образом, в зависимости от аудитории правомерно употреблять в качестве аргументов то или иное множество высказываний. Такое множество высказываний, приемлемых для данной аудитории в качестве несомненно истинных – для доказательства некоторого утверждения – или в качестве правдоподобных, когда речь идет лишь о более или менее достаточном подтверждении, а также совокупность приемлемых логических средств, – называется полем аргументации.
3. Промежуточные допущения – вспомогательные допущения, которые вводятся в процесс рассуждения (дедукции) и устраняются затем при переходе к окончательному результату рассуждения.
Промежуточные допущения в силу их вспомогательной роли вводятся в доказательство обычно исходя из логической структуры тезиса. Они могут быть как истинными, так и ложными, поскольку, например, в так называемых доказательствах «от противного» вводятся – в качестве промежуточных допущений – обычно даже заведомо ложные высказывания.
4. Форма доказательства (демонстрация) – логический способ обоснования тезиса при помощи аргументов, возможно, с использованием промежуточных допущений.
Доказательством такого способа обоснования тезиса обычно является дедуктивный вывод, т. е. вывод, обеспечивающий истинность заключения – тезиса, при истинности посылок – аргументов доказательства. Основу такого рода дедуктивного рассуждения составляет совокупность принятых законов логики и правил перехода от одних высказываний к другим в процессе доказательства. Указание на характер этих переходов называется демонстрацией. Значительно реже встречаются недедуктивные доказательства, где демонстрация выступает в форме индуктивного умозаключения или вывода по аналогии.
Виды доказательств
Основными видами доказательств, различающимися по форме, являются доказательства прямыеи косвенные(непрямые).
1. Прямыедоказательства представляют собой дедуктивный вывод, в котором тезис непосредственно выводится из аргументов в качестве заключения вывода.
2. Косвенное (непрямое)доказательство истинности или ложности некоторого высказывания состоит в том, что оно достигается посредством опровержения некоторых других высказываний.
Выделяются два вида косвенных(непрямых) доказательств: доказательство «от противного», или апагогическое, и доказательство посредством исключения альтернатив.
Основное отличие косвенныхдоказательств от прямыхсостоит в том, что в прямомдоказательстве в качестве посылок вывода используются только аргументы, в то время как косвенноедоказательство использует также и вспомогательные допущения.
• Доказательство «от противного» осуществляется посредством применения непрямого правила рассуждения:

Для доказательства истинности «А» при наличии множества аргументов «Г» предполагается ложность этого высказывания, т. е. истинность «⎤А», и показывается, что из «Г» и этого предположения выводимо противоречие «В» и «⎤В». Указанное правило позволяет заключить при этом, что из аргументов «Г» выводимо «А». Для доказательства истинности «⎤А» или так называемого «непрямого опровержения» используется несколько иная схема:
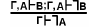
Опровержение такого рода характеризуется как опровержение путем «сведения к абсурду». Однако следует отметить, что, по существу, в любом доказательстве «от противного» мы имеем в качестве его составной части указанную выше форму опровержения путем «сведения к абсурду».
• Доказательство посредством исключения альтернатив состоит в том, что, например, для доказательства некоторого высказывания используется в качестве аргумента дизъюнктивное высказывание, т. е. перечисление всех альтернатив.
Обобщенная форма подобных доказательств такова:
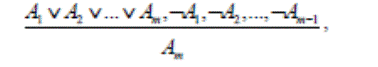
где m≥2, «Am» – тезис доказательства.
Из схемы видно, что условием истинности дизъюнктивного аргумента «A1, …, Am» является перечисление именно всех возможностей, среди которых тезис и все его возможные альтернативы.
Данное правило рассуждения, лежащее в основе косвенного(непрямого) доказательства посредством исключения альтернатив, является обобщением дедуктивной формы разделительно-категорического силлогизма, а именно отрицающее-утверждающего модуса данного силлогизма (modus tollendo ponens):
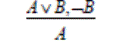
Дата добавления: 2016-02-09; просмотров: 1032;
