Фигуры и модусы простого категорического силлогизма

• В зависимости от того, какое место – субъекта или предиката – в посылках занимает средний термин, различают четыре разновидности силлогизма, называемые фигурами простого категорического силлогизма. Каждая фигура имеет свои специальные правила, хотя эти правила могут быть получены строго логически, как следствия из

общих правил простого категорического силлогизма.

Первая фигура характеризуется тем, что средний термин (M) играет в ней роль субъекта в большей и предиката в меньшей посылке. Первая фигура простого категорического силлогизмаиспользуется в процессе познания как способ распространения некоторого общего знания, выраженного в большей посылке, на некоторые особые случаи –класс предметов выражаемых меньшим термином (S). В связи с этим данную фигуру характеризуют как способ подведения класса Sпод класс M, относительно которого имеется общее знание. Правила первой фигуры:

1. Большая посылка – общее суждение.

2. Меньшая посылка – утвердительное суждение.

II. Вторая фигура характеризуется тем, что средний термин (M) играет роль предиката в обеих посылках. Данная фигура используется в основном как средство опровержения некоторых неправильных подведений чего-либо под некоторое понятие.

Правила второй фигуры:

1. Большая посылка должна быть общим суждением.

2. Одна из посылок должна быть отрицательным суждением.

III. В третьей фигуре средний термин (M) играет роль субъекта в обеих посылках. В основном третья фигура может применяться в качестве способа опровержения необоснованных обобщений.

Правила третьей фигуры:

1. Меньшая посылка должна быть утвердительным суждением.

2. Заключение – частное суждение.

IV. В четвертой фигуре средний термин (М) является предикатом в большей и субъектом в меньшей посылке. Данная фигура представляет собой искусственное построение и не имеет никаких определенных познавательных функций.

Правила четвертой фигуры:

1. Если одна из посылок – отрицательное, то большая посылка – общее суждение.

2. Если большая посылка – утвердительное суждение, то меньшая – общее суждение.

3. Если меньшая посылка – утвердительное суждение, то заключение – частное суждение.

Все четыре фигуры простого категорического силлогизма можно представить в виде графических схем:

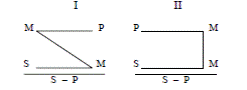
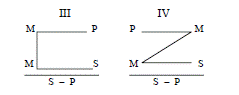
• Модусы– это разновидности силлогизма внутри каждой фигуры, различающиеся характером суждений, – посылок и заключения, – составляющих силлогизм. Учитывая наличие четырех типов категорических суждений – общеутвердительных (A), общеотри

цательных (E), частноутвердительных (I) и частноотрицательных (O) – можно подсчитать, что в каждой фигуре имеется 64, а всего (для всех четырех фигур) – 256 модусов. Однако не все они представляют собой правильные умозаключения. Таких – правильных модусов– всего лишь 24, т. е. по 6 модусовв каждой фигуре. Среди них выделяется 19 основных или так называемых сильных модусов, которые полностью удовлетворяют общим правилам простого категорического силлогизмаи специальным правилам фигур. Остальные – слабые модусы– могут быть представлены как сложные выводы: сочетания выводов в форме категорического силлогизма с выводами по правилам «логического квадрата».