Лекция 2. Первое начало термодинамики и термохимия

2.1. Вводная часть

Термодинамика – это наука о теплоте и ее превращениях. Она возникла в конце восемнадцатого века в результате интереса к повседневно встречающимся процессам превращения работы, теплоты и материи. Первые количественные термодинамические эксперименты были поставлены для выяснения тепла трения, возникающего при сверлении орудийных стволов (Б. Томпсон). В термодинамике наиболее известны такие имена, как Дж. Блэк, А. Лавуазье, Г. Гесс, Л. Карно, Дж. Джоуль, Дж, Максвел, Р. Клаузиус, У. Кельвин, Г. Гельмгольц, Л. Больцман, Я. Вант-Гофф, Дж. Гиббс.

Ранние работы по термодинамике были посвящены описанию количественных соотношений между теплотой и другими формами энергии. В настоящее время в этой области научных исследований наблюдается сдвиг от анализа энергетических изменений, сопровождающих превращения материи, в сторону использования термодинамики в качестве инструмента, необходимого для понимания и предсказания поведения систем в связи с их энергетическими характеристиками.

Особенно важные перемены произошли после создания статистической термодинамики. Статистическая термодинамика имеет дело с поведением самих молекул, а не с макроскопическими системами типа паровых двигателей или такими процессами, как перегонка, кристаллизация, электролиз. В статистической термодинамике сначала изучают отдельные атомы и молекулы, а затем их коллективное поведение. В классической термодинамике изучают только свойства макроскопических тел в целом, а отдельные частицы не рассматривают. Оба подхода очень много дают химику и биохимику, но мы пока ограничимся освоением лишь классических подходов. С помощью термодинамики, или энергетики, как ее иногда называют, есть возможность предсказать максимальную работу, которую можно получить в определенном процессе, определить состояние равновесия, максимально возможный выход, оптимальную температуру и давление для данной реакции, выбрать лучший растворитель. Термодинамика может ответить на вопрос о том, будет ли реакция протекать в нужном направлении. Но термодинамика не может предсказать необходимое для этого время, указать на механизм реакции. Например, используя термодинамику, можно утверждать, что при температуре возгорания бензин способен самопроизвольно реагировать с кислородом, выделяя двуокись углерода, воду, тепло. Эта реакция предпочтительна. Можно вычислить, сколько при сгорании выделилось тепла.

Однако термодинамика не отвечает на вопрос о том, какова величина теплового барьера, который должен быть преодолен для того, чтобы реакция пошла самопроизвольно, т.е. термодинамика изучает в основном конечные, равновесные состояния. Скорости и механизм реакции рассматривают в разделе «Кинетика».

2.2. Некоторые понятия, используемые в термодинамике

Под понятием энергия обычно понимают способность производить работу. Решая какую-либо задачу методами термодинамики, необходимо прежде всего выделить из окружающего мира какую-то систему. Это может быть дождевая капля, двигатель, организм, планета и т.д. Если говорят, что выделенная система гомогенна, это означает, что свойства системы одинаковы во всех частях, и система непрерывна от точки к точке. Если говорят, что система гетерогенна, это означает, что в ней присутствует не менее двух областей, называемых фазами, которые отделены друг от друга поверхностями, называемыми границами раздела. Системы бывают трех типов: открытые, закрытые и изолированные. В закрытой системе во время процесса происходит изменение энергии, но масса остается постоянной. В открытой системе может изменяться как энергия, так и масса. В изолированной системе не происходит обмена с окружающей средой ни массой, ни энергией!

Очень часто в термодинамике сталкиваются с понятием равновесие. Если состав и свойства системы достаточно долго не меняются, то говорят, что система находится в равновесии. Однако химическое равновесие не является состоянием покоя. Это состояние, в котором реакция протекает как в одну, так и в другую сторону, но с одинаковыми скоростями.

Состояние системы определяется ее свойствами. Если изменяется одно из свойств, состояние системы меняется. При изучении системы обычно рассматриваются такие свойства, которые легко измерить. Это, в частности, температура, давление, объем, состав. Некоторые свойства взаимосвязаны, поэтому нет необходимости измерять их все одновременно.

К сожалению, наши знания и возможности не позволяют вычислить (определить) весь запас энергии системы. Поэтому используется сравнительный подход. Часто энергия системы сравнивается с каким-либо стандартом (стандартным состоянием). Например, газ обычно сравнивается с идеальным газом при стандартных условиях, жидкий растворитель – с чистой жидкостью, твердое вещество – с его наиболее стабильной кристаллической формой. Такие состояния, называемые стандартными, представляют собой точки отсчета, относительно которых измеряют изменение в системе.

2.3. Формулировка первого начала термодинамики

Первое начало термодинамики – это закон сохранения энергии. Он впервые четко сформулирован Г. Гельмгольцем в 1847 году. Этот закон не может быть четко доказан, но является результатом всего человеческого опыта. Такие законы часто называют законами природы. Известный математик А. Пуанкаре как-то иронически заметил, что в сущности все твердо верят в закон сохранения энергии потому, что математики принимают его за экспериментальный факт, а экспериментаторы считают его математической теоремой.

Есть несколько формулировок первого закона термодинамики. Если одна из них принимается в качестве основной, то все другие являются следствиями, вытекающими из нее.

Одна из формулировок звучит следующим образом: энергия не создается и не уничтожается. Возможны лишь превращения энергии из одного вида в другой в строго эквивалентных количествах.

Следствием из этого закона является вывод, что невозможен вечный двигатель первого рода, т.е. нельзя создать такой двигатель, который совершил бы работу без затраты энергии. Создание такого двигателя возможно только в том случае, если неверен первый закон.

Часто используется еще одна формулировка первого начала термодинамики: внутренняя энергии изолированной системы есть величина постоянная.

Если данной системе передается некоторое количество энергии в форме тепла Q, которое идет только на приращение внутренней энергии системы DU и на совершение системой работы W, то, согласно первому началу,

Q = DU + W, (2.1)

для бесконечно малых изменений

dQ = dU + dW. (2.2)

Уравнения (2.1) и (2.2) являются математическим выражением первого начала термодинамики.

Укажем, что DU и dU не зависят от пути перехода системы из начального состояния в конечное, т.е. внутренняя энергия является функцией состояния системы.

Справедливость этого утверждения можно доказать следующим образом (рис. 2.1).

Предположим, что в состоянии (I) внутренняя энергия системы U₁. Из этого состояния система переходит в состояние (2), в котором ее внутренняя энергия равна U₂.

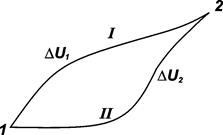
Рис. 2.1. Схематическое отображение путей перехода системы из состояния 1 в состояние 2 и обратно

При переходе системы из состояния 1 в состояние 2 по пути I обозначим изменение внутренней энергии системы как DU₁, а по второму пути, – как DU₂. Согласно первому закону, DU₁ = DU₂ . Если бы это равенство не соблюдалось, а, например, DU₁ было бы больше DU₂, то, переводя систему из состояния 1 в состояние 2 по пути I и обратно по пути II, можно было бы получать энергию из ничего. Это противоречит первому началу термодинамики.

В отличие от DU величины Q и W в общем случае зависят от пути процесса. Поэтому в уравнении (2.2) dU является полным дифференциалом, в то время как dQ и dW – просто бесконечно малыми величинами

2.4. Применение первого начала термодинамики
к различным процессам

Если система совершает работу W только против внешнего давления, то

W = РDV (2.3)

или для элементарного процесса

dW = pdV. (2.4)

Математическое выражение первого начала термодинамики в этом случае имеет вид:

Q= DU + pD (2.5)

или

dQ = dU + pdV. (2.6)

Для изохорного процесса (V = const) pDV = 0 и следовательно:

Q_V = DU, (2.7)

dQ_V = dU, (2.8)

где Q_V – теплота, сообщаемая системе в изохорном процессе.

Из уравнений (2.7) и (2.8) следует, что в изохорном процессе тепло, сообщаемое системе, идет только на приращение внутренней энергии системы. В этом случае Q_V не зависит от пути перехода системы из одного состояния в другое и dQ_V является полным дифференциалом, т.е. функцией состояния.

Это означает, что изменение внутренней энергии системы DU в изохорном процессе определяется теплотой процесса Q_V и может быть измерено калориметрически.

В случае изобарного процесса (р= const)

Q_P = DU + PDV, (2.9)

Q_p = U₂ - U₁ + pV₂ -pV_1, (2.10)

где Q_P – теплота, сообщаемая системе в изобарном процессе. Сгруппируем величины с одинаковыми индексами

Q_P = (U₂ + PV₂ ) - (U₁+ PV₁). (2.11)

Так как внутренняя энергия, объем системы и давление – функции состояния, то сумма величин U + pV также должна быть функцией состояния и ее изменение не зависит от пути перехода системы из одного состояния в другое.

Эту функцию состояния называют энтальпией и обозначают символом Н.

Н = U + pV. (2.12)

Из уравнений (2.11 ) и (2.12) следует, что

Q_p = DН, (2.13)

dQ_р = dH. (2.14)

Таким образом, в изобарном процессе все тепло, сообщенное системе, идет на приращение ее энтальпии. В этом случае Q_p также не зависит от пути перехода системы из одного состояния в другое и dQ_р является полным дифференциалом.

Из уравнений (2.13) и (2.14) следует также, что изменение энтальпии системы DН в изобарном процессе определяется теплотой процесса Q_p и может быть измерено калориметрически.

В адиабатном процессе, т.е. в процессе, в котором система не обменивается с окружающей средой теплотой, работа совершается за счет уменьшения внутренней энергии системы:

Q = 0 , (2.15)

dQ = 0, (2.16)

W = - DU, (2.17)

dW = - dW. (2.18)

Изотермический процесс характеризуется T = const. для такого процесса dU = 0, тогда dQ = dW_T, т.е. вся сообщенная системе теплота превращается в работу, величина которой определяется уравнениями

dW_T = pdv, (2.19)

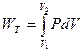. (2.20)

Используя уравнение состояния газа Менделеева-Клапейрона, найдем, что для 1 моль идеального газа

,

тогда

. (2.21)

2.5. Теплота химической реакции (общие положения)

Химические процессы обычно сопровождаются поглощением или выделением тепла. Реакции с выделением тепла называются экзотермическими, реакции с поглощением тепла – эндотермическими. Количество тепла пропорционально массе прореагировавших веществ, поэтому сравнение количества тепла, выделяющегося в реакции, относят к единице количества вещества. Обычно это 1 моль. Экспериментально теплоты химических реакций определяют при постоянном объеме Q_v или постоянном давлении Q_p.

Установим связи между Q_p и Q_v.

В соответствии с уравнением (2.12) имеем:

DН = DU + pDV,

но из уравнений (2.13) и (2.7) следует, что

Q_p = DН, а DН = DU, то Q_p = Q_v + pDV.

Если вещества газообразны и подчиняются уравнению Клапейрона-Менделеева, тогда pV₁ = n₁RT, a pV₂ = n₂RT. Следовательно,

pDV = n₂RT - n₁RT=Q_p =Q_v + DnRT, (2.22)

где Dn = Sn_i - Sn_j , т.е. сумма продуктов минус сумма исходных веществ.

Другими словами, Dn – изменение числа молей реагирующих веществ в результате протекания реакции.

Из уравнения (2.22) следует, что если число молей в результате реакции не меняется, то Q_p = Q_v .

Если реакция протекает в конденсированной системе, то объем системы меняется мало и в этом случае Q_p и Q_v приблизительно равны.

2.6. Закон Гесса

Изучая тепловые эффекты разных химических реакций, русский ученый Г.М. Гесс в 1840 году установил закон, который назван его именем: теплота химической реакции, протекающей при постоянном объеме или постоянном давлении, определяется только природой исходных веществ и продуктов и не зависит от числа и последовательности промежуточных стадий при условии, что теплоты измерены при одинаковых температурах.

Интересно, что закон Гесса был открыт раньше установления первого начала термодинамики. После установления первого начала стало ясно, что закон Гесса является одним из следствий этого начала, согласно которому Q_v = DU и Q_p = DH, где DU и DH – функции состояния и не зависят от пути процесса. Закон Гесса имеет большое практическое значение, так как позволяет рассчитать теплоты химических реакций, для которых они не могут быть определены экспериментально или это очень сложно сделать. Обычно для этого решают систему термохимических уравнений.

Термохимическим называют такое уравнение, в котором в правой части наряду с химическими формулами продуктов реакции указывают теплоту реакции. При этом для реагирующих веществ указывается агрегатное состояние участников реакции. Если вещество в твердом состоянии существует в нескольких полиморфных модификациях, то необходимо указать эту модификацию.

Стехиометрические коэффициенты могут быть и дробными, так как они указывают молярные количества реагирующих веществ.

С термохимическими уравнениями можно проводить такие же математические операции, как и с алгебраическими. Например, превращение глюкозы в молочную кислоту при анаэробной ферментации используется некоторыми микроорганизмами для получения энергии.

Непосредственно измерить теплоту этого процесса трудно, поскольку параллельно с молочной кислотой образуются и другие продукты.

Однако можно экспериментально определить теплоты следующих реакций:

1. С₆Н₁₂О_{6 (Т)} + 6О₂ → 6CO_{2 (Г)} + 6 Н₂О _(Ж) – 2808кДж;

2. СН₃СН(ОН)СООН _(Ж) + 3О_{2 (Г)} → 3СО_{2 (Г)} + 3Н₂О _(Ж) – 321кДж;

3. С₆Н₁₂О_{6 (Т)} + aqua → С₆Н₁₂О_{6 (aqua)} + 10,7 кДж.

Вычитая из уравнения 1 удвоенное 2 и затем 3, получим:

С₆Н₁₂О_{6 (Т)} - 2СН₃СН(ОН)СООН _(Ж) +6О_{2 (Г)} - 6О_{2 (Г)} - С₆Н₁₂О_{6 (Т)} =

6CO_{2 (Г)} - 6CO_{2 (Г)} + 6Н₂О _(Ж) - 6Н₂О _(Ж) - С₆Н₁₂О_6(aqua) – 2808 +2×321 – 10,7.

После сокращения: 2СН₃СН(ОН)СООН _(Ж) → С₆Н₁₂О_{6 (aqua)} – 2155,3 кДж.

2.7. Следствие из закона Гесса

Расчеты теплот химических реакций с использованием закона Гесса значительно упрощают, если воспользоваться так называемыми стандартными теплотами образования и стандартными теплотами горения.