Температура и нулевой закон термодинамики

Изучение физической химии часто начинают с законов поведения газов. Связано это с тем, что законы поведения газов представляют собой основу для понимания поведения более сложных систем, поскольку в той или иной мере, с определенными допущениями, все системы могут быть мысленно или экспериментально упрощены. Такое упрощение часто называют моделированием определенных свойств сложной системы. Поведение газов относительно просто по двум причинам:

1. Смеси газов всегда образуют однородные по составу, истинные растворы, находящиеся в одной «фазе».

2. При одной и той же температуре и одном и том же давлении одинаковые объемы газов содержат одинаковое количество молекул (это известный закон Авогадро).

Системы газов характеризуются общими параметрами – такими, как масса, объем, температура, давление, плотность и др. Некоторые параметры связаны между собой. Это означает, что если мы, например, знаем массу и объем газа, то нам не представляет труда вычислить его плотность, так как

плотность = масса/объем.

Напомним, что, рассматривая свойства газов, мы пренебрегаем влиянием внешних полей. Экспериментаторы стремятся обойтись минимальным числом параметров (свойств), так как их непосредственное измерение резко увеличивает трудозатраты на эксперимент.

По-видимому, не следует объяснять, что подразумевается под такими свойствами, как масса, объем, плотность, давление. Наиболее трудно воспринимается понятие температуры. То, что мы обычно понимаем под температурой, есть не что иное, как мера средней кинетической энергии молекул некоего тела. Если рассматривать перенос тепла от одного тела к другому, то это представляет собой просто передачу кинетической энергии молекул одного тела другому. Однако такие понятия температуры и тепла были приняты далеко не сразу. Вы помните, что ранее тепло рассматривалось как некая невидимая «калорическая» жидкость – теплород, которая перетекает от одного тела к другому. Забегая вперед, укажем, что состояние газа обусловлено любыми двумя из трех его свойств: P, V, T. Иначе говоря, из трех переменных независимыми являются только две. Математически мы можем записать это в форме

T = f (P,V) (эмпирическая температура). (1.1)

Определение температуры, которое следует из выражения 1.1, часто называют нулевым законом термодинамики. Нулевой закон термодинамики часто выражают через понятие температуры и теплового равновесия: две системы, находящиеся в тепловом равновесии с третьей, находятся в тепловом равновесии друг с другом.

Допустим, что два тела, нагретые до разных температур, приводятся в контакт друг с другом до наступления равновесия.

Это значит, что

f(P1,V1) = f(P2,V2) или T1= T2. (1.2)

На практике это означает, что одно тело может быть использовано для определения температуры другого тела. Это легко видеть из уравнения. Допустим, у нас сохраняется одинаковым давление для двух тел, т.е. Р1= Р2,тогда после установления равновесия по изменению объема можно судить о температуре анализируемого образца. На этом принципе работают известные нам термометры. Для этого берется любое тело или жидкость, которые линейно расширяются с температурой, их калибруют, выбирая удобную шкалу. В повседневной практике обычно используют стоградусную шкалу Цельсия, в которой за ноль принимается температура плавления льда, а за 100 °С – температура кипения воды. Все это при атмосферном давлении.

1.2. Законы поведения идеальных газов:
уравнение состояния идеального газа

Два очень важных закона, известных как закон Бойля и закон Шарля, были открыты экспериментально. Их называют эмпирическими законами. Так, в 1662 году Р. Бойль измеряет степень сжатия атмосферного воздуха в U‑образной трубке, короткий конец которой был прокалиброван и запаян. В длинный конец можно было добавлять ртуть. Высота воздушного столба А была пропорциональна объему. Оказалось, что произведение Р´А было приблизительно постоянным. Р – высота ртутного столба. Из этого был сделан вывод, что при неизменной температуре

P1V1= P2V2.(1.3)

Это и есть закон Бойля.

Закон Шарля (он одновременно был открыт Ж.Л. Гей-Люссаком) тоже был найден эмпирически. Сегодня он гласит:

В процессе охлаждения газа при постоянном давлении на каждый градус Цельсия его объем уменьшается на 1/273,15 того объема, который он занимает при 0 °С.

Математически это можно записать уравнением

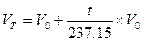(при постоянном давлении). (1.4)

Чем интересно это уравнение? Оно указывает, что при t = -273,15 °С газ вообще должен исчезать, т.е. не занимать никакого объема. Это невероятно. Понятно, что это уравнение не может выполняться точно. Тем не менее температура -273,15 °С получила название абсолютного нуля. Абсолютный ноль использован в качестве точки отсчета в шкале Кельвина (или абсолютной шкале).

Приведенное выше уравнение можно записать так:

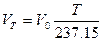,где T = t + 273,15. (1.5)

При объединении законов Бойля и Шарля мы получим уравнение, которое позволяет характеризовать поведение газа при изменении всех трех параметров – температуры, давления, объема.

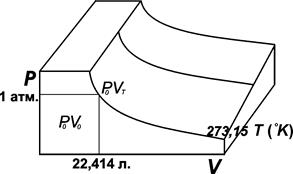
Рис. 1.1. PV-изотермы идеального газа

Точка P₀V₀находится на изотерме (так называется кривая, полученная при одной и той же температуре), отвечающей 0 °С (рис. 1.1). В этой точке давление равно 1атм, а объем для газа равен 22,414 л. Этот объем при нормальных условиях (0 °С, 1 атм.) занимает 1 моль газа. Если двигаться по изобаре (т.е. по линии, соответствующей одному и тому же давлению), то эта траектория описывается уравнением Шарля

.

Умножим обе части уравнения на Р₀

.

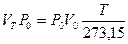Но по закону Бойля

V_ТРо=Р V,

тогда

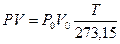(при постоянной температуре),

т.е. если двигаться по изотерме.

Сейчас обозначим 273,15 как Т₀и получим хорошо известное уравнение, объединяющее уравнение Бойля и Шарля:

. (1.6)

Как мы уже видели, 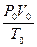представляет собой постоянную величину, которая является коэффициентом пропорциональности, переводящим градусы абсолютной шкалы в единицы энергии. Действительно, PV имеет размерность энергии. Полученный коэффициент обозначают величиной R, и он носит название универсальной газовой постоянной. В результате мы получим уравнение идеального газа или уравнение Менделеева-Клайперона:

Р 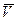= RТ (для 1 моля газа, где 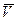молярный объем), (1.7)

PV = nRT (для n молей газа). (1.8)

Название этого уравнения уже говорит о том, что оно верно для идеального газа и, наоборот, газ является идеальным, когда точно подчиняется этому уравнению. В реальном газе необходимо учитывать, что сами его молекулы занимают определенный объем. Кроме того, между молекулами газа имеются силы притяжения.

Рассмотрим первую часть уравнения. PV имеет размерность энергии. Действительно, допустим, что давление выражено в дин/см², а объем в см³. Произведение PV имеет размерность дин/см, а это есть не что иное, как эрг, т.е. единица энергии в системе СГС (сантиметр/грамм/секунда). Аналогично PV можно выразить в Дж (система СИ)

В принципе энергию в любой форме можно представить в виде двух множителей: один из них будет фактором интенсивности, а другой – емкости.

Например, для уравнения идеального газа фактор интенсивности – это давление, а емкости – объем; в выражении кинетической энергии фактором емкости является масса, а половина квадрата скорости – интенсивность. В случае электрической энергии фактор емкости – это заряд, а фактор интенсивности – потенциал.

В принципе различные формы энергии легко можно переводить один в другой. Однако необходимо помнить, что ни в коем случае не допускается приравнивание друг к другу отдельных сомножителей, т.е. отдельно факторов интенсивности или факторов емкости.

Для того, чтобы отличать факторы емкости и факторы интенсивности, полезно помнить, что фактор интенсивности не зависит от размеров и протяженности системы.

Хотелось бы сказать, что коэффициент пропорциональности (R) очень удобен для перехода от одного типа энергии к другому. Более подробно мы с этим познакомимся на практических занятиях.

Здесь же укажем, что

R = 8,314 10⁷ эрг/моль × град;

R = 8,314 Дж/моль×град;

R = 1,987 кал/моль×град.

Газовая постоянная тесно связана с теплоемкостью газов. Теплоемкость – это количество тепла, необходимое для повышения температуры вещества на 1°. Обычно речь идет о молярной теплоемкости, т.е. она относится к количеству вещества в один моль. Удельная теплоемкость относится к одному грамму, т.е. это количество тепла, необходимого для нагрева 1 г вещества на 1°. Количество тепла, необходимого для нагрева вещества, зависит не только от его массы, но и от условий нагрева. Поэтому различают молярную теплоемкость при постоянном объеме и при постоянном давлении . Для жидкостей и твердых тел и практически одинаковы. Для газа больше на то количество тепла, которое затрачивается на расширение газа. Для одноатомных газов » 5 ккал/град, а » 1 кал/град. ` – = 2 кал/град » R. Для многоатомных такая зависимость не сохраняется. Обусловлено это тем, что подводимая энергия переходит не только в поступательную, но и в колебательную и вращательную энергию.

1.3. Кинетическое уравнение газов

Мы подчеркивали, что законы Бойля и Шарля получены эмпирическим, опытным путем. Однако эти уравнения могут быть выведены и теоретически. Еще в 1738 году Бернулли теоретическим путем пришел к закону Бойля, рассматривая процесс столкновения молекул газа со стенками сосуда. Совокупность представлений о температуре и давлении газов как проявление движения молекул называют кинетической теорией газов.

В этом случае давление рассматривается как результат бомбардировки молекулами стенок сосуда, а температура считается пропорциональной средней энергии поступательного движения молекул.

Для вывода уравнения необходимо ввести ряд упрощений.

1. Молекулы пренебрежимо малы по сравнению с разделяющими их расстояниями.

2. Отсутствует взаимодействие между молекулами.

3. Молекулы движутся по прямым линиям и испытывают идеально упругие столкновения друг с другом и со стенками сосуда.

Это означает, что при столкновении молекул их средняя кинетическая энергия сохраняется до тех пор, пока температура остается постоянной. Эти условия практически соблюдаются в случае малых плотностей газа.

Рассмотрим простую систему из N молекул газа, каждая из которых имеет массу m. Температура системы Т. Молекулы находятся в коробке кубической формы с ребром, равным а. Молекулы двигаются со скоростями v1, v2, v3 . . . vN. Понятно, что молекулы могут двигаться в разных направлениях. Это можно представить как движение в системе координат x, y, z, совпадающих с ребрами куба. Для молекул эти скорости будут vx1, vx2, vx3 . . . vxN; Vy1, vy2, vy3 . . . vyN; vz1, vz2, vz3 . . . vzN:

V12 = Vx1 2 + Vy12 + Vz12;

V22 = Vx2 2 + Vy22 + Vz22;

V32 = vx3 2 + vy32 + vz32;

vN2 = vxN2 + vyN2 + vzN2.

Cреднеквадратичная скорость молекул будет равна:

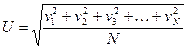. (1.9)

C одной и той же стенкой молекула будет сталкиваться через каждые 2а. Если ее скорость вдоль оси х равна vxсм/сек, то она будет ударять об эту стенку vx/2а раз в секунду. После каждого столкновения молекула будет отскакивать с такой же скоростью vx, не теряя кинетической энергии. Кинетический момент (импульс) молекулы равен произведению массы на скорость, а скорость изменения импульса во времени есть не что иное, как сила.

Действительно, основное уравнение механики f = ma, где а – ускорение. Ускорение равно изменению скорости во времени dv/dt, тогда сила равна mdv/dt или f = d(mv)/dt.

Импульс молекулы до столкновения был mvx, а после стал -mvx. Изменение импульса одного столкновения равно 2mvx. Молекула сталкивается со стенкой vx/2а раз в секунду. Тогда

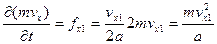. (1.10)

Полная сила, действующая на стенку со стороны всех N молекул, равна сумме сил, действующих со стороны каждой отдельной молекулы:

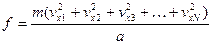, (1.11)

а давление – это сила, действующая на единицу площади, т.е. на а², тогда

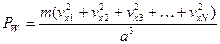, (1.12)

но а³ равно объему куба;

. (1.13)

То же самое можно написать для других осей.

После группировки получим:

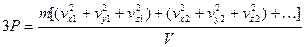. (1.14)

Принимая во внимание уравнение для квадратичной скорости, получим:

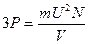или 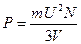(1.15)

или

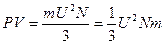, (1.16)

где N – число молекул в сосуде, а U – среднеквадратичная скорость молекул.

Поскольку N и m – постоянны, а скорость молекулы является функцией лишь температуры, то понятно, что

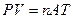. (1.17)

Любые виды энергии легко переводятся друг в друга с использованием газовой постоянной R и числа молей газа, следовательно

PV = nRT.

1.4. Уравнение состояния реальных (неидеальных) газов.
Уравнение Ван-дер-Ваальса

Речь уже шла о том, что свойства реальных газов редко полностью могут быть описаны законами, выведенными для идеальных газов. Это особенно касается состояний при высоких давлениях и низких температурах. В этих условиях объем системы становится относительно малым и необходимо учитывать собственный объем молекул. Кроме того, начинают действовать силы межмолекулярного притяжения. Для идеального газа произведение PV является постоянным.

Рис. 1.2 показывает, что поведение О₂, Н₂ и CO₂ отклоняется от поведения идеального газа. Причем вид отклонения зависит от природы газа.

Рис. 1.2. Отклонение в поведении реальных газов от идеального в условиях высоких давлений

Чтобы как-то устранить причины, из-за которых уравнение идеального газа практически неприменимо для описания поведения реальных газов, Ван-дер-Ваальс в 1879 году предложил включить в него два дополнительных члена – а и b: константу а добавляют к Р для того, чтобы учесть (скомпенсировать) уменьшение давления из-за межмолекулярного притяжения; константа b учитывает эффективный объем молекул газа, и она вычитается из 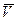. Обе константы подбирались эмпирически. В результате для одного моля газа уравнение приобретает вид:

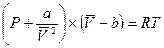. (1.18)

Однако в этом уравнении появились еще некоторые члены. Так, поправка к давлению принята равной 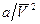по той причине, что молекулы на поверхности газа притягиваются не только друг к другу (к молекулам на поверхности), но и к молекулам, находящимся внутри. Сила притяжения зависит от плотности газа как на поверхности, так и внутри. Поскольку плотность – это масса/V, то ее влияние можно учесть умножением константы а на 1/V2. Поправка b в реальном случае примерно в 4 раза превышает собственный объем молекул моля газа. Ее иногда называют исключенным объемом, так как она соответствует пространству, реально исключаемому одним молем плотно упакованных молекул. Поправки а и b для любого газа приводятся в расчете на 1 моль. Если количество газа больше или меньше одного моля, необходимо пользоваться следующим уравнением

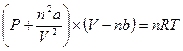. (1.19)

В практике при расчетах обычно используются табличные данные по значениям а и b.

Это важно в некоторых случаях при расчетах метаболических процессов, в результате которых выделяется, например, СО₂.

Однако в большинстве случаев при метаболических процессах давление выделившегося газа относительно невелико. Поэтому ошибка при использовании уравнения, применимого к идеальному газу, для расчетов поведения реальных газов находится в пределах 1-2%. Это меньше, чем стандартная ошибка большинства экспериментов, и поэтому в обычных условиях уравнение Ван-дер-Ваальса используется редко.

1.5. Закон парциальных давлений Дальтона

Зато очень часто в практике необходимо использование закона Дальтона, или закона парциальных давлений. Он основан на том, что в смеси газов каждый газ оказывает такое же давление, какое он оказывал бы, если бы в сосуде присутствовал один.

Давление компонентов газовой смеси зависит только от числа молей каждого из них, так как температура и объем для всех газов в смеси одинаковы.

Давление каждого из газов называют парциальным давлением. Согласно закону парциальных давлений Дальтона, общее давление газовой смеси равно сумме парциальных давлений:

Pобщ= P1+ P2+ P3+ ... + PN. (1.20)

Если V – общий объем, а n1, n2, n3и т.д. – число молей каждого компонента, то

PV=n1RT+n2RT+n3RT+...+nNRT=RT(n1+n2+n3+...+nN). (1.21)

Парциальное давление одного из газов, допустим 1, будет равно

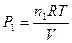. (1.22)

Понятно, что отношение парциального давления газа к его общему давлению равно отношению числа молей этого компонента к числу молей всех газов в смеси:

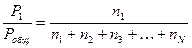. (1.23)

Это отношение называют молярной долей и обозначают символом Х. Для газа 1 молярная доля равна Х1и т.д. Парциальное давление учитывается во многих расчетах. Например, операции по измерению объемов, включающих сбор газов над поверхностью воды, требуют учета парциального давления паров воды в газовой смеси. По сравнению с водяными парами пары ртути имеют значительно более низкое давление, и это создает ощутимые преимущества при использовании ртути в качестве вытесняемой жидкости, так как парциальным давлением паров ртути в таких расчетах вполне можно пренебречь.

С другой стороны, хорошо известно, что вдыхаемый нами воздух является смесью газов. Выдыхаемый воздух отражает происходящий в легких процесс газового обмена. Он насыщен парами воды. Парциальное давление водяного пара достаточно заметно и равно приблизительно 48 мм.р.с. Поэтому, если общее давление выдыхаемого воздуха равно 760 мм, то давление, обусловленное смесью газов О₂ + СО₂ + N₂, будет равно не 760, а 760 – 48 = 712 мм.р.с.