Построение и использование хеш-функций

Под термином хеш-фунция понимается функция, отображающая электронные сообщения произвольной длины (иногда длина сообщения ограничена, но достаточно большим числом), в значения фиксированной длины. Последние часто называют хеш-кодами. Таким образом, у всякой хеш-функции h имеется большое количество коллизий, т.е. пар значений х и у таких, что h(x)=h(y).Основное требование, предъявляемое криптографическими приложениями к хеш-функциям, состоит в отсутствии эффективных алгоритмов поиска коллизий. Хеш-функция, обладающая таким свойством, называется хеш-функцией, свободной от коллизий. Кроме того, хеш-функция должна быть односторонней, т.е. функцией, по значению которой вычислительно трудно найти ее аргумент, в то же время, функцией, для аргумента которой вычислительно трудно найти другой аргумент, который давал бы то же самое значение функции [16].

Схемы электронной цифровой подписи – основная сфера применения хеш-функций. Поскольку используемые на практике схемы электронной подписи не приспособлены для подписания сообщений произвольной длины, а процедура, состоящая в разбиении сообщения на блоки и генерации подписи для каждого блока по отдельности, крайне неэффективна, единственным разумным решением представляется применение схемы подписи к хеш-коду сообщения. Таким образом, хеш-функции вместе со схемами электронной цифровой подписи предназначены для решения задач обеспечения целостности и достоверности передаваемых и хранимых на носителях информации электронных сообщений. В прикладных информационных системах требуется применение так называемых криптографически стойких хеш-функций. Под термином «криптографически стойкая хэш-функция» понимается функция h,которая является односторонней и свободной от коллизий.

Введем следующие обозначения Хеш-функция h обозначается как h(α) и h(α,β) для одного и двух аргументов, соответственно. Хеш-код функции h обозначается как Н. При этом Н₀ = 1 обозначает начальное значение (вектор инициализации) хеш-функции. Под обозначением 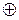будет пониматься операция сложения по модулю 2 или логическая операция XOR («Исключающая ИЛИ»). Результат шифрования блока В блочным шифром на ключе k обозначается E_k(B).

Для лучшего понимания дальнейшего материала приведем небольшой пример построения хеш-функции

Предположим нам необходимо подписать при помощи заданного алгоритма электронной цифровой подписи достаточно длинное сообщение М. Вкачестве шифрующего преобразования в хеш-функции будет использоваться процедура шифра DES с ключом k. Тогда, чтобы получить хеш-код Н сообщения М при помощи хеш-функции h,необходимо выполнить следующую итеративную операцию:

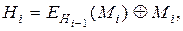
где 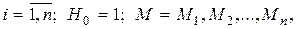сообщение М разбито на n 64-битных блока.

Хеш-кодом данной хеш-функции является значение Н = h(M,I)= Н_п.

Таким образом, на вход схемы электронной цифровой подписи вместо длинного сообщения М (как правило, несколько сотен или тысяч байтов) подается хэш-код H_n, длина которого ограничена длиной блока шифра DES, т.е. 64 битами. При этом в силу криптографической стой кости используемой хеш-функции практическая стойкость самой схемы подписи будет оставаться той же, что и при подписи сообщения М,в то время как эффективность всего процесса подписи электронного сообщения будет резко увеличена.

Были предприняты попытки построения хеш-функций на базе блочного шифра с размером хеш-кода в k раз (как правило, k = 2) большим, чем размер блока алгоритма шифрования.

В качестве примера можно привести хеш-функции МDС2 и MDC4 фирмы IBM. Данные хеш-функции используют блочный шифр (в оригинале DES) для получения хеш-кода, длина которого в 2 раза больше длины блока шифра. Алгоритм MDC2 работает несколько быстрее, чем MDC4, но представляется несколько менее стойким.

В качестве примера хеш-функций, построенных на основе вычислительно трудной математической задачи, можно привести функцию из рекомендаций МККТТ Х.509.

Криптографическая стойкость данной функции основана на сложности решения следующей труднорешаемой теоретико-числовой задачи. Задача умножения двух больших (длиной в несколько сотен битов) простых чисел является простой с вычислительной точки зрения, в то время как факторизация (разложение на простые множители) полученного произведения является труднорешаемой задачей для указанных размерностей.

Следует отметить, что задача разложения числа на простые множители эквивалентна следующей труднорешаемой математической задаче. Пусть n = pq произведение двух простых чисел р и q. В этом случае можно легко вычислить квадрат числа по модулю п: x²(mod n), однако вычислительно трудно извлечь квадратный корень по этому модулю.

Таким образом, хеш-функцию МККТТ Х.509 можно записать следующим образом:

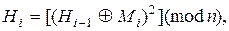
где .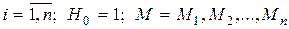

Длина блока M_i представляется в октетах, каждый октет разбит пополам и к каждой половине спереди приписывается полуоктет, состоящий из двоичных единиц: n – произведение двух больших (512-битных) простых чисел р и q.

Ниже приведен числовой пример использования данной хеш-функции в его упрощенном варианте.

Пример 9.14.Получить хеш-код для сообщения «HASHING» при помощи хеш-функции Х.509 с параметрами р = 17, q = 19.

Порядок вычисления хеш-кода:

а) получить значения модуля: n = pq = 323;

б)представить сообщение «HASHING» в виде символов ASCII:

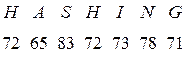
в) представить коды ASCII битовой строкой:

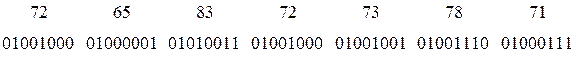
г) разбить байт пополам (разбиение октета на полуоктеты), добавить в начало полубайта единицы и получить хешируемые блоки М_i:

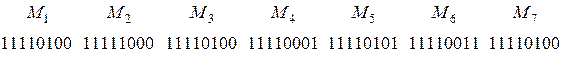
д) выполнить итеративные шаги:

первая итерация:

M₁ = 11110100

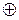
H₀ = I = 00000000

H₀ 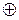M₁ = 11110100₂ = 244₁₀

[(H₀ 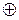M₁)]²(mod 323) = 244²(mod323) = 104

H₁ = 104₁₀ = 01101000₂

вторая итерация:

М₂ = 11111000

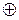
H₁ = 01101000

H₁ 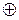М₂ = 10010000₂ = 144₁₀

[(H₁ 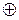М₂)]²(mod 323) = I44²(mod323) = 64

H₂ = 64₁₀ = 01000000₂

………… … ……….

i-я итерация...

Пример легко продолжить самостоятельно.

Пример 9.15 (упрощенный вариант).Хешируемое слово «ДВА». Коэффициенты р =7, q = 3. Вектор инициализации Н₀ = 1 выберем равным 6 (выбирается случайным образом). Определим n = pq = 7·3 = 21. Слово «ДВА» в числовом эквиваленте можно представить как 531 (по номеру буквы в алфавите). Тогда хеш-код сообщения 531 получается следующим образом:

первая итерация:

М₁ + Н₀ = 5 + 6 = 11; [M₁ + Н₀]² (mod n) = 11² (mod 21) = 16 = Н₁;

вторая итерация:

М₂ + Н₁= 3 + 16 = 19; [M₂ + Н₁]² (mod n) = 19² (mod 21) = 4 = Н₂;

третья итерация:

М₃ + Н₂ = 1 + 4 = 5; [М₃ + Н₂]² (mod п) = 5² (mod 21) = 4 = Н₃.

В итоге получаем хеш-код сообшения «ДВА», равный 4.

9.10. ГОСТ 28147-89 – стандарт на шифрование данных.

В Республике Беларусь установлен единый алгоритм криптографического преобразования данных для систем обработки информации в сетях ЭВМ, отдельных вычислительных комплексах и ЭВМ, который определяется ГОСТ 28147-89.

Алгоритм криптографического преобразования данных предназначен для аппаратной или программной реализации, удовлетворяет криптографическим требованиям и не накладывает ограничений на степень секретности защищаемых сообщений (информации). Из-за сложности этого алгоритма здесь будут приведены только основные его концепции. Чтобы подробно изучить алгоритм криптографического преобразования, следует обратиться к ГОСТ 28147-89 . Приведенный ниже материал должен использоваться лишь как ознакомительный.

При описании алгоритма приняты следующие обозначения. Если L и
R – это последовательности бит, то LR будет обозначать конкатенацию последовательностей L и R. Под конкатенацией последовательностей L и R понимается последовательность бит, размерность которой равна сумме размерностей L и R. В этой последовательности биты последовательности R следуют за битами последовательности L. Конкатенация битовых строк является ассоциативной, т.е. запись ABCDE обозначает, что за битами последовательности А следуют биты последовательности В, затем С и т.д.

Символом (+) обозначается операция побитового сложения по модулю 2, символом [+] – операция сложения по модулю 2³² двух 32-разрядных чисел. Числа суммируются по следующему правилу:

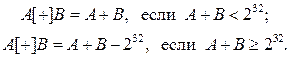
Символом {+} обозначается операция сложения по модулю 2³² – 1 двух
32-разрядных чисел. Правила суммирования чисел следующие:

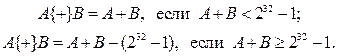
Алгоритм криптографического преобразования предусматривает несколько режимов работы. Но в любом случае для шифрования данных используется ключ, который имеет размерность 256 бит и представляется в виде восьми 32-разрядных чисел X(i). Если обозначить ключ через W, то

W = Х(7)Х(6)Х(5)Х(4)Х(3)Х(2)Х(1)Х(0).

Расшифрование выполняется по тому же ключу, что и зашифрование, но этот процесс является инверсией процесса зашифрования данных.

Первый и самый простой режим –замена. Открытые данные, подлежащие зашифрованию, разбивают на блоки по 64 бит в каждом, которые можно обозначить T(j). Очередная последовательность бит T(j) разделяется на две последовательности В(0) (левые или старшие биты) и A(0) (правые или младшие биты), каждая из которых содержит 32 бита. Затем выполняется итеративный процесс шифрования, который описывается следующими формулами:

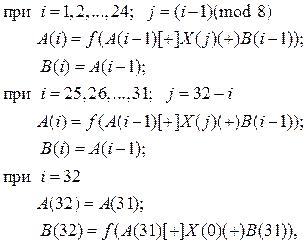
где i обозначает номер итерации (i = 1, 2,…, 32).

Функция f называется функцией шифрования. Ее аргументом является сумма по модулю 2³² числа А(i), полученного на предыдущем шаге итерации, и числа X(j) ключа (размерность каждого из этих чисел равна 32 знакам).

Функция шифрования включает две операции над полученной 32-разрядной суммой. Первая операция называется подстановкой К. Блок подстановки K состоит из восьми узлов замены K(1)...K(8) с памятью 64 бит каждый. Поступающий на блок подстановки 32-разрядный вектор разбивается на восемь последовательно идущих 4-разрядных векторов, каждый из которых преобразуется в 4-разрядный вектор соответствующим узлом замены, представляющим собой таблицу из шестнадцати целых чисел в диапазоне 0...15.

Входной вектор определяет адрес строки в таблице, число из которой является выходным вектором. Затем 4-разрядные выходные векторы последовательно объединяются в 32-разрядный вектор. Таблицы блока подстановки К содержат ключевые элементы, общие для сети ЭВМ и редко изменяемые.

Вторая операция – циклический сдвиг влево 32-разрядного вектора, полученного в результате подстановки К 64-разрядный блок зашифрованных данных Т_ш представляется в виде:

Т_ш = A(32)B(32).

Остальные блоки открытых данных в режиме простой замены зашифровываются аналогично.

Следует иметь в виду, что режим простой замены допустимо использовать для шифрования данных только в ограниченных случаях.

К этим случаям относится выработка ключа и зашифрование его с обеспечением имитозащиты для передачи по каналам связи или хранения в памяти ЭВМ.

Следующий режим шифрования называется режимом гаммирования. Открытые данные, разбитые на 64-разрядные блоки Т(i) (i =1, 2,..., m, где m определяется объемом шифруемых данных), зашифровываются в режиме гаммирования путем поразрядного сложения по модулю 2 с гаммой шифра Г_ш, которая вырабатывается блоками по 64 бит, т.е.

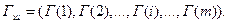
Число двоичных разрядов в блоке Т(т) может быть меньше 64, при этом неиспользованная для шифрования часть гаммы шифра из блока Г(m) отбрасывается.

Уравнение зашифрования данных в режиме гаммирования может быть представлено в следующем виде:

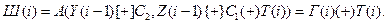
В этом уравнении Ш(i) обозначает 64-разрядный блок зашифрованного текста; А(-) – функцию шифрования в режиме простой замены (аргументами этой функции являются два 32-разрядных числа); С₁ и С₂ – константы, заданные в обязательном приложении 2 к ГОСТ 28147-89. Величины У(-) и Z(•) определяются итерационно по мере формирования гаммы следующим образом (Y(0), Z(0)) = A(S), где S – 64-разярдная двоичная последовательность (синхропосылка)

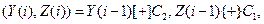
где i = 1, 2,…, m.

Расшифрование данных возможно только при наличии синхропосылки, которая не является секретным элементом шифра и может храниться в памяти ЭВМ или передаваться по каналам связи вместе с зашифрованными данными.

Режим гаммирования с обратной связью очень похож на режим гаммирования Как и в режиме гаммирования, открытые данные, разбитые на 64-разрядные блоки T(i) (i = 1, 2,..., m, где m определяется объемом шифруемых данных), зашифровываются путем поразрядного

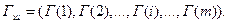
сложения по модулю 2 с гаммой шифра Г_ш, которая вырабатывается блоками по 64 бит.

Число двоичных разрядов в блоке Т(т) может быть меньше 64, при этом неиспользованная для шифрования часть гаммы шифра из блока Г(m) отбрасывается.

Уравнение зашифрования данных в режиме гаммирования с обратной связью для г= 2,3,..., то может быть представлено в следующем виде:

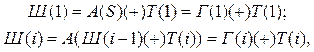
где Ш(i) обозначает 64-разрядный блок зашифрованного текста; A(-) – функцию шифрования в режиме простой замены.

Аргументом функции на первом шаге итеративного алгоритма является 64-разрядная синхропосылка, а на всех последующих – предыдущий блок зашифрованных данных Ш(i – 1).

В ГОСТ 28147-89 определяется процесс выработки имитовставки, который единообразен для любого из режимов шифрования данных. Имитовставка – это блок из р бит (имитоставка И_р), который вырабатывается либо перед шифрованием всего сообщения, либо параллельно с шифрованием по блокам. Первые блоки открытых данных, которые участвуют в выработке имитовставки, могут содержать служебную информацию (например адресную часть, время, синхропосылку) и не зашифровываться. Значение параметра р (число двоичных разрядов в имитовставке) определяется криптографическими требованиями с учетом того, что вероятность навязывания ложных помех равна 1/2^р.

Для получения имитовставки открытые данные представляются в виде 64-разрядных блоков T(i) (i = 1, 2 m, где m определяется объемом шифруемых данных). Первый блок открытых данных Т(1) подвергается преобразованию, соответствующему первым 16 циклам алгоритма зашифрования в режиме простой замены, причем в качестве ключа для выработки имитовставки используется ключ, по которому шифруются данные

Полученное после 16 циклов работы 64-разрядное число суммируется по модулю 2 с вторым блоком открытых данных Т(2). Результат суммирования снова подвергается преобразованию, соответствующему первым 16 циклам алгоритма зашифрования в режиме простой замены.

Полученное 64-разрядное число суммируется по модулю 2 с третьим блоком открытых данных Т(3) и т д. Последний блок Т(m), при необходимости дополненный до полного 64-разрядного блока нулями, суммируется по модулю 2 с результатом работы на шаге m-1, после него зашифровывается в режиме простой замены по первым 16 циклам работы алгоритма. Из полученного 64-разрядного числа выбирается отрезок И_р длиной р бит.

Имитовставка И_р передается по каналу связи или в память ЭВМ после зашифрованных данных. Поступившие зашифрованные данные расшифровываются и из полученных блоков открытых данных Т(i) вырабатывается имитовставка И_р, которая затем сравнивается с имитовставкой И_р, полученной из канала связи или из памяти ЭВМ В случае несовпадения имитовставок все расшифрованные данные считают ложными.