Криптосистема без передачи ключей
В информационных сетях использование традиционных систем шифрования с ключом затрудненно необходимостью иметь специальный особо защищенный способ для передачи ключа. В 1976 году У. Диффи (Diffie W.) и М. Хеллман (Hellman M.) - инженеры-электрики из Станфордского университета, а также студент Калифорнийского университета Р. Меркль (Merkle R.), предложили новый принцип построения криптосистем, не требующий передачи ключа принимающему сообщение и сохранения в тайне метода шифрования. В дальнейшем, в качестве примеров, рассмотрим три системы, основанные на идеях Диффи и Хеллмана: без передачи ключей, с открытым ключом и электронную подпись - все они в свою очередь основаны на математическом фундаменте теории чисел.
Пусть абоненты А, В, С,... условились организовать между собой секретную переписку. Для этой цели они выбирают достаточно большое простое число  такое, что
такое, что 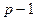 хорошо разлагается на не очень большие простые множители. Затем каждый из абонентов независимо один от другого выбирает себе некоторое натуральное число, взаимно простое с
хорошо разлагается на не очень большие простые множители. Затем каждый из абонентов независимо один от другого выбирает себе некоторое натуральное число, взаимно простое с 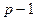 . Пусть число абонента А -
. Пусть число абонента А -  , абонента В - b и т.д. Числа
, абонента В - b и т.д. Числа  , b,... составляют первые секретные ключи соответствующих абонентов. Вторые секретные ключи (
, b,... составляют первые секретные ключи соответствующих абонентов. Вторые секретные ключи (  для А,
для А, 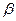 для В и т.д.) находятся из уравнений: для А из
для В и т.д.) находятся из уравнений: для А из 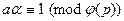 ,
, 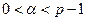 ; для В – из
; для В – из  ,
, 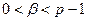 и т.д. Пересылаемые сообщения, коды-числа, должны быть меньше
и т.д. Пересылаемые сообщения, коды-числа, должны быть меньше 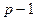 . В случае, когда сообщение больше или равно
. В случае, когда сообщение больше или равно 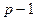 , оно разбивается на части таким образом, чтобы каждая часть была числом, меньшим
, оно разбивается на части таким образом, чтобы каждая часть была числом, меньшим 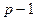 .
.
Предположим абонент А решил отправить сообщение 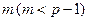 В. Для этого он сначала зашифровывает свое сообщение ключом
В. Для этого он сначала зашифровывает свое сообщение ключом  а, получая по формуле
а, получая по формуле 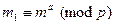 шифрованное сообщение
шифрованное сообщение 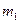 , которое отправляется В. В, получив
, которое отправляется В. В, получив 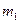 , зашифровывает его своим ключом
, зашифровывает его своим ключом 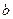 , получая по формуле
, получая по формуле 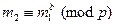 шифрованное сообщении
шифрованное сообщении 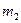 , которое отправляется обратно к А. А шифрует полученное сообщение ключом
, которое отправляется обратно к А. А шифрует полученное сообщение ключом  по формуле
по формуле 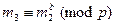 и окончательно отправляет
и окончательно отправляет 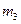 к В. В, используя ключ
к В. В, используя ключ 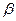 , сможет теперь расшифровать исходное сообщение т. Действительно,
, сможет теперь расшифровать исходное сообщение т. Действительно, 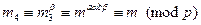 , т.к.
, т.к. 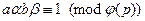 , следовательно,
, следовательно,  для некоторого целого
для некоторого целого 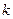 и
и 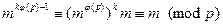 , т.к.
, т.к. 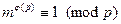 по теореме Эйлера-Ферма.
по теореме Эйлера-Ферма.
Пример 9.12.Абоненты А и В вместе выбрали 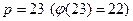 , А выбрал
, А выбрал 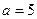 , а В -
, а В - 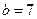 . Затем из уравнения
. Затем из уравнения 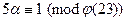 A находит
A находит 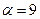 , а В из подобного уравнения находит
, а В из подобного уравнения находит 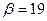 . При передаче сообщения
. При передаче сообщения 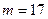 от А к В сначала А отправляет к В
от А к В сначала А отправляет к В 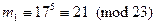 , из
, из 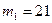 В вычисляет
В вычисляет 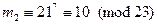 и отправляет его обратно А, из
и отправляет его обратно А, из 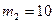 А вычисляет для В
А вычисляет для В  , наконец, В может прочитать посланное ему сообщение
, наконец, В может прочитать посланное ему сообщение 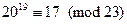 .
.
Дата добавления: 2016-02-04; просмотров: 4874;
