ФОРМУЛЫ ДЛЯ ЗАПОМИНАНИЯ

ТМЖГ

• Манометрическое (или избыточное) давление (Па) – это превышение абсолютного давления над атмосферным:

.

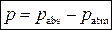Нормальное атмосферное давление p_atm = 1,013·10⁵ Па.

• Вакуумметрическое давление (или вакуум) – это разность между атмосферным давлением и абсолютным давлением в точке, когда абсолютное давление меньше атмосферного:

.

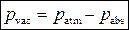• Основное уравнение гидростатики: давление в некоторой точке покоящейся жидкости равняется сумме давления p₀, приложенного к свободной поверхности жидкости, и давления столба жидкости γh над этой точкой:

,

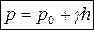где h – глубина (м), на которой находится точка, γ = ρg = 1000·9,81 = 9810 Н/м³ – удельный вес (вес единицы объёма).

• Гидравлический радиус сечения (м) – отношение площади живого сечения (м²) к смоченному периметру (м):

R = ω/χ.

Для напорного течения в трубе диаметром D гидравлический радиус R = D/4.

• Уравнение неразрывности потока: если между двумя сечениями нет притока и оттока воды, то расход (м³/с) для этих сечений одинаков:

Q₁ = Q₂ или V₁ω₁ = V₂ω₂,

где V – средняя скорость по сечению.

• Число Рейнольдса для круглой трубы диаметром D

Re = VD/ν,

где ν – кинематическая вязкость; для воды при t = 20°C ν = 10^-6 м²/с. Для русел некруглого сечения и безнапорных труб, как и в других формулах вместо D подставляем эквивалентный диаметр D_eq = 4R.

• Уравнение Бернулли: полный напор в сечении выше по течению равняется полному напору в сечении ниже по течению плюс потери напора h:

.

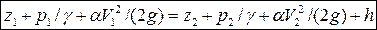Напор (м) – это удельная (на единицу веса) энергия: геометрический напор z – потенциальная энергия положения, напор давления p/γ – потенциальная энергия давления, скоростной напор αV²/(2g) – кинетическая энергия. Корректив кинетической энергии (коэффициент Кориолиса) α учитывает неравномерность распределения скоростей по сечению. Для турбулентного движения α = 1,1.

• Пьезометрический уклон – это уклон пьезометрической линии (линии удельной потенциальной энергии), соединяющей отметки пьезометров:

.

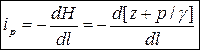• Гидравлический уклон – это уклон напорной линии (линии полной удельной энергии), соединяющей отметки гидродинамических напоров (отметки гидродинамических трубок):

.

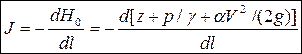При равномерном движении в открытых руслах гидравлический уклон J равняется пьезометрическому уклону i_p, а также уклону i поверхности потока и дна русла: J = i_p = i.

• Потери напора на трение по длине в круглой напорной трубе в соответствии с обобщённой формулой Дарси-Вейсбаха прямо пропорциональны длине трубы l и скоростному напору 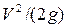и обратно пропорциональны диаметру трубы D:

,

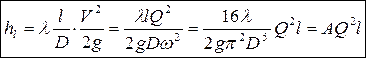где λ – гидравлический коэффициент трения, A – удельное сопротивление трубы (с²/м⁶).

• Гидравлический коэффициент трения для турбулентного течения рассчитывается по формуле Альтшуля

,

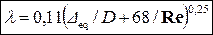где Δ_eq/D – относительная шероховатость трубы, Δ_eq – эквивалентная шероховатость (мм).

• Сопротивление (с²/м⁵) трубы длиной l:

.

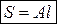• Принцип сложения потерь напора: напор в начале трубопровода равняется сумме потерь напора на всех участках плюс свободный напор H_fr, который надо иметь на конце трубопровода:

.

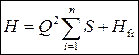• Потери напора на местном сопротивлении даются формулой Вейсбаха:

,

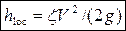где V – средняя скорость в сечении ниже по течению после местного сопротивления, ζ – коэффициент местного сопротивления.

• Расход истечения через отверстие или патрубок

,

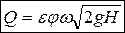где ε – коэффициент сжатия, φ – коэффициент скорости, ω – площадь отверстия, H – напор на отверстии.