Определения расхода воды в русле реки по результатам промеров
Вариант задания, выполняемый студентом, определяется по номеру зачётной книжки.
2.1. Из табл. 2.1 берётся зависимость глубины h в створе реки от расстояния x от постоянного начала на берегу для различных вариантов y (предпоследняя цифра номера зачётной книжки).
Таблица 2.1
| x | y | |||||||||
| 2,23 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
| 2,50 | 1,05 | 0,78 | 1,52 | 0,55 | 1,17 | 0,48 | 1,14 | 1,62 | 1,07 | 0,88 |
| 3,00 | 1,55 | 1,05 | 2,10 | 0,78 | 1,55 | 1,14 | 1,78 | 2,20 | 1,67 | 1,15 |
| 3,50 | 1,85 | 1,23 | 2,52 | 0,99 | 1,77 | 1,78 | 2,15 | 2,52 | 1,87 | 1,33 |
| 4,00 | 2,10 | 1,45 | 2,88 | 1,23 | 2,15 | 2,45 | 2,45 | 2,14 | 2,10 | 1,49 |
| 4,50 | 2,55 | 1,50 | 2,99 | 1,48 | 2,67 | 2,17 | 2,88 | 2,15 | 2,43 | 1,57 |
| 5,00 | 2,88 | 1,48 | 3,17 | 1,98 | 2,78 | 2,10 | 3,15 | 2,13 | 2,55 | 1,47 |
| 5,50 | 3,15 | 1,42 | 2,88 | 2,15 | 2,55 | 2,18 | 3,25 | 2,05 | 2,37 | 1,46 |
| 6,00 | 2,87 | 1,37 | 2,52 | 2,35 | 2,60 | 2,05 | 3,05 | 2,00 | 2,14 | 1,47 |
| 6,50 | 2,24 | 1,15 | 2,14 | 2,15 | 2,88 | 1,67 | 2,54 | 1,88 | 1,99 | 1,23 |
| 7,00 | 2,25 | 0,87 | 1,89 | 1,80 | 2,15 | 1,20 | 2,17 | 1,76 | 1,53 | 1,17 |
| 7,50 | 1,70 | 0,55 | 1,53 | 1,67 | 1,78 | 1,14 | 1,80 | 1,53 | 1,42 | 1,08 |
| 8,00 | 1,15 | 0,48 | 1,20 | 1,20 | 1,55 | 0,98 | 1,75 | 1,22 | 1,05 | 0,76 |
| 8,50 | 0,76 | 0,35 | 0,87 | 0,80 | 0,75 | 0,45 | 1,05 | 0,78 | 0,98 | 0,53 |
| 8,89 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
2.2. Из табл. 2.2 берётся распределение скоростей по ширине и глубине в створе реки, где hm – глубина дна на данной скоростной вертикали, z – последняя цифра номера зачётной книжки.
Таблица 2.2
| x, м | ||||||
| 0,1hm | 0,60(z + 1) | 0,62(z + 1) | 0,64(z + 1) | 0,82(z + 1) | 0,88(z + 1) | 0,73(z + 1) |
| 0,2hm | 0,59(z + 1) | 0,61(z + 1) | 0,63(z + 1) | 0,80(z + 1) | 0,86(z + 1) | 0,71(z + 1) |
| 0,6hm | 0,54(z + 1) | 0,56(z + 1) | 0,58(z + 1) | 0,72(z + 1) | 0,75(z + 1) | 0,64(z + 1) |
| 0,8hm | 0,50(z + 1) | 0,52(z + 1) | 0,54(z + 1) | 0,63(z + 1) | 0,66(z + 1) | 0,58(z + 1) |
| 0,9hm | 0,47(z + 1) | 0,48(z + 1) | 0,50(z + 1) | 0,56(z + 1) | 0,58(z + 1) | 0,52(z + 1) |
2.3. Рассмотрим порядок выполнения задания на конкретном примере. По отметкам дна h и горизонтальным координатам промерных вертикалей строим поперечный профиль русла (рис. 2.1)
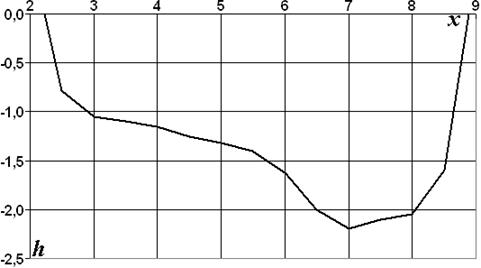 Рис. 2.1
Рис. 2.1
| x | h |
| 2,23 | 0,00 | |
| 2,50 | 0,78 | |
| 3,00 | 1,05 | |
| 3,50 | 1,10 | |
| 4,00 | 1,15 | |
| 4,50 | 1,25 | |
| 5,00 | 1,32 | |
| 5,50 | 1,40 | |
| 6,00 | 1,62 | |
| 6,50 | 2,00 | |
| 7,00 | 2,20 | |
| 7,50 | 2,10 | |
| 8,00 | 2,05 | |
| 8,50 | 1,60 | |
| 8,89 | 0,00 |
2.4. Вычисляем площадь водного сечения 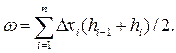
ω = [0,27(0,00+0,78)+0,5(0,78+1,05)+…+0,39(1,60+0,00)]/2 = 9,63 м2.
2.5. Ширина реки
В = xn – x0 = 6,66 м.
2.6. Средняя глубина
hср = ω/B = 9,63/6,66 = 1,45 м.
2.7. Строим профили скоростных вертикалей. Батометр (рис. 2.2) не может измерять скорость на поверхности реки и на дне. Поэтому эти скорости определяем графической экстраполяцией.
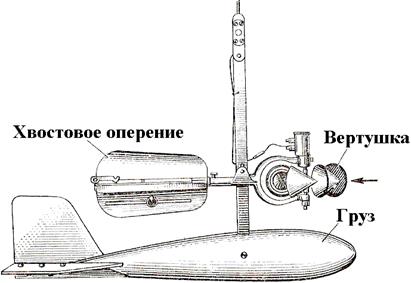
Рис. 2.2
2.8. Результаты измерения скоростей при х = 3,00 м
| h, м | u, м/с | 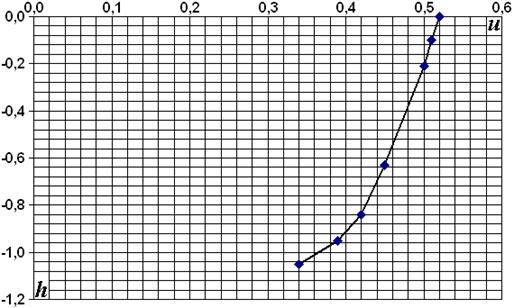
|
| 0,00 | 0,52 | |
| 0,10 | 0,51 | |
| 0,21 | 0,50 | |
| 0,63 | 0,45 | |
| 0,84 | 0,42 | |
| 0,95 | 0,39 | |
| 1,05 | 0,34 |
Рис. 2.3
Средняя скорость на вертикали 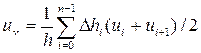 ;
;
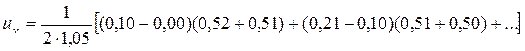 = 0,456 м/с.
= 0,456 м/с.
2.9. Результаты измерения скоростей при х = 4,00 м
| h, м | u, м/с | 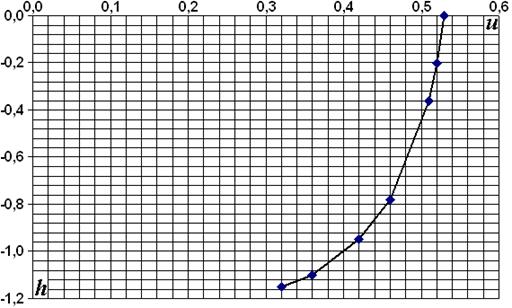
|
| 0,00 | 0,53 | |
| 0,20 | 0,52 | |
| 0,36 | 0,51 | |
| 0,63 | 0,46 | |
| 0,78 | 0,42 | |
| 0,95 | 0,36 | |
| 1,15 | 0,32 |
Рис. 2.4
Средняя скорость на вертикали uv = 0,471 м/с.
2.10. Результаты измерения скоростей при х = 5,00 м
| h, м | u, м/с | 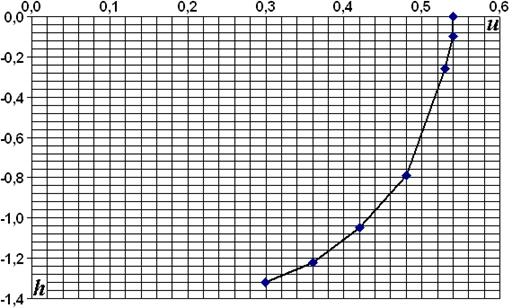
|
| 0,00 | 0,54 | |
| 0,10 | 0,54 | |
| 0,26 | 0,53 | |
| 0,79 | 0,48 | |
| 1,05 | 0,42 | |
| 1,22 | 0,36 | |
| 1,32 | 0,30 |
Рис. 2.5
Средняя скорость на вертикали uv = 0,472 м/с.
2.11. Результаты измерения скоростей при х = 6,00 м
| h, м | u, м/с | 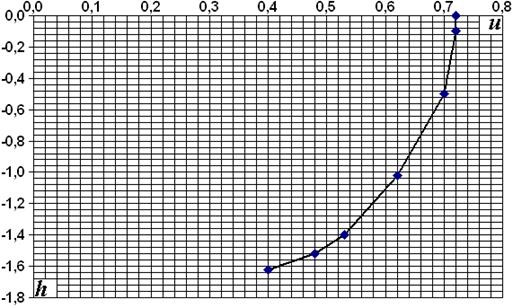
|
| 0,00 | 0,72 | |
| 0,10 | 0,72 | |
| 0,50 | 0,70 | |
| 1,02 | 0,62 | |
| 1,40 | 0,53 | |
| 1,52 | 0,48 | |
| 1,62 | 0,40 |
Рис. 2.6
Средняя скорость на вертикали uv = 0,631 м/с.
2.12. Результаты измерения скоростей при х = 7,00 м
| h, м | u, м/с | 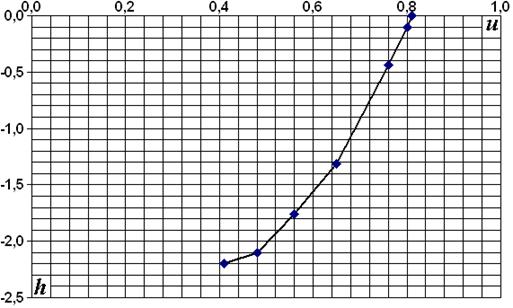
|
| 0,00 | 0,81 | |
| 0,10 | 0,80 | |
| 0,44 | 0,76 | |
| 1,31 | 0,65 | |
| 1,76 | 0,56 | |
| 2,10 | 0,48 | |
| 2,20 | 0,41 |
Рис. 2.7
Средняя скорость на вертикали uv = 0,660 м/с.
2.13. Результаты измерения скоростей при х = 8,00 м
| h, м | u, м/с | 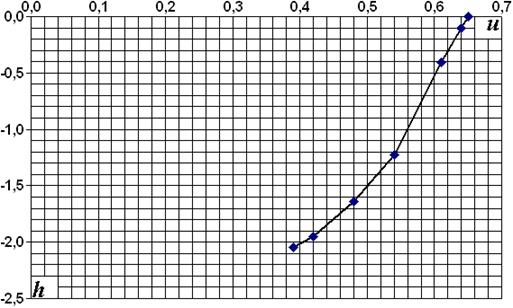
|
| 0,00 | 0,65 | |
| 0,10 | 0,64 | |
| 0,41 | 0,61 | |
| 1,23 | 0,54 | |
| 1,64 | 0,48 | |
| 1,95 | 0,42 | |
| 2,05 | 0,39 |
Рис. 2.8
Средняя скорость на вертикали uv = 0,546 м/с.
2.14. Сводим в таблицу (табл. 2.3) данные для построения графиков распределения глубины h, скорости vв, и удельного расхода q на вертикали (рис. 2.9). В промежуточных точках (0,5 м, 1,5 м и т. д.) скорость на вертикали находим как полусумму скоростей в соседних точках. Например, на вертикали х = 3,5 м скорость
vв = (0,47 + 0,63)/2 = 0,55 м/с.
2.15. Удельный (на единицу длины) расход на вертикали находим, перемножая глубину и скорость на вертикали. Например, на вертикали х = 3,5 q = h vв = 1,40·0,55 = 0,77 м³/с/м.
Таблица 2.3
| x, м | Δx, м | h, м | vв, м/с | q, м³/с/м |
| 2,23 | 0,00 | 0,00 | 0,00 | |
| 2,50 | 0,27 | 0,78 | 0,23 | 0,18 |
| 3,00 | 0,50 | 1,05 | 0,46 | 0,48 |
| 3,50 | 0,50 | 1,10 | 0,46 | 0,51 |
| 4,00 | 0,50 | 1,15 | 0,47 | 0,54 |
| 4,50 | 0,50 | 1,25 | 0,47 | 0,59 |
| 5,00 | 0,50 | 1,32 | 0,47 | 0,62 |
| 5,50 | 0,50 | 1,40 | 0,55 | 0,77 |
| 6,00 | 0,50 | 1,62 | 0,63 | 1,02 |
| 6,50 | 0,50 | 2,00 | 0,65 | 1,29 |
| 7,00 | 0,50 | 2,20 | 0,66 | 1,45 |
| 7,50 | 0,50 | 2,10 | 0,60 | 1,27 |
| 8,00 | 0,50 | 2,05 | 0,55 | 1,12 |
| 8,50 | 0,50 | 1,60 | 0,27 | 0,44 |
| 8,89 | 0,39 | 0,00 | 0,00 | 0,00 |
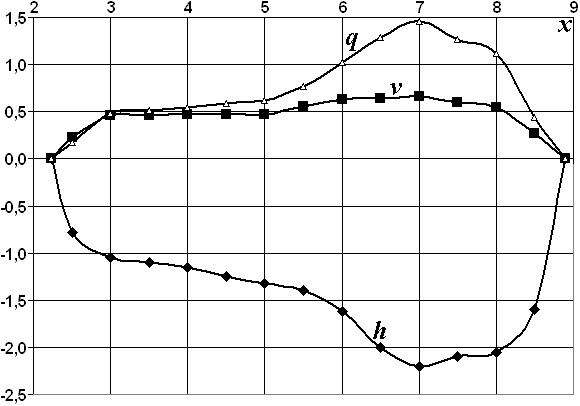
Рис. 2.9
2.16. Находим расход воды в данном сечении 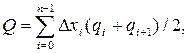
Q = 0,27(0 + 0,18)/2 + 0,5(0,18 + 0,48)/2 + … = 5,10 м³/с.
2.17. Средняя скорость в сечении
V = Q/ω = 5,10/9,63 = 0,53 м/с.
3. Гидравлический расчёт нагорной канавы на ливневый сток
Величины исходных данных определяются по предпоследней y и последней z цифрам номера зачётной книжки.
Исходные данные: район Донецка; поверхность и вид грунта водосборной площади – задернованная глина (для такой поверхности из табл. 3.1 коэффициент шероховатости 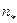 = 0,04; из табл. 3.2 коэффициент стока ψ = 0,20); средний уклон водосбора в направлении стока дождевых вод
= 0,04; из табл. 3.2 коэффициент стока ψ = 0,20); средний уклон водосбора в направлении стока дождевых вод 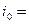 0,03 + 0,001y; длина канавы lк = 1400 + 100z м; уклон канавы по дну i = 0,004; коэффициент заложения откосов m = 1,5.
0,03 + 0,001y; длина канавы lк = 1400 + 100z м; уклон канавы по дну i = 0,004; коэффициент заложения откосов m = 1,5.
Требуется выполнить гидравлический расчет канавы в сечении, проходящем через точку В на рис. 3.1.
Расчёт производится в соответствии с рекомендациями инструкции «Руководство по проектированию водоотвода и дренажа на летных полях аэродромов» [12].
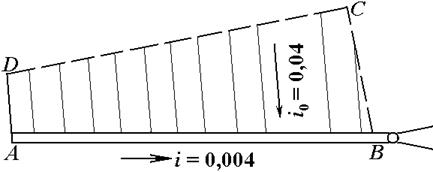
Рис. 3.1
Таблица 3.1
| Вид поверхности | Коэффициент шероховатости 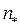
|
| Асфальтовое покрытие Бетонное покрытие Грунтовая поверхность без грунтового покрова Задернованная грунтовая поверхность Неукреплённые земляные русла (канавы) | 0,011 0,014 0,025 0,04…0,06 0,02…0,025 |
Таблица 3.2
| Вид поверхности | Коэффициент стока ψ |
| Кровли и асфальтобетонные покрытия Брусчатые мостовые Булыжные мостовые Щебёночные покрытия Гравийные садово-парковые дорожки Грунтовые поверхности (спланированные) Газоны | 0,95 0,6 0,45 0,4 0,3 0,2 0,1 |
Пример расчёта выполнен для следующих данных: средний уклон водосбора в направлении стока дождевых вод 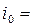 0,04; длина канавы lк = 1200 м; уклон канавы по дну i = 0,004; коэффициент заложения откосов m = 1,5.
0,04; длина канавы lк = 1200 м; уклон канавы по дну i = 0,004; коэффициент заложения откосов m = 1,5.
По карте находим для района Донецка интенсивность дождя продолжительностью 20 мин с вероятным периодом превышения один раз в год 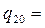 88 л/с/га (рис. 3.2). По табл. 3.3 находим для востока Украины среднее количество дождей за год
88 л/с/га (рис. 3.2). По табл. 3.3 находим для востока Украины среднее количество дождей за год 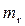 = 60, показатель степени γ = 1,82, для периода однократного превышения расчетной интенсивности дождя P ≥ 1 год показатель степени n = 0,67.
= 60, показатель степени γ = 1,82, для периода однократного превышения расчетной интенсивности дождя P ≥ 1 год показатель степени n = 0,67.
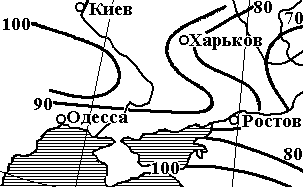
Рис. 3.2
Таблица 3.3
| Район | Значение n при | mr | g | |
| Р ³ 1 | Р < 1 | |||
| Равнинные области Украины | 0,71 | 0,64 | 1,54 | |
| Восток Украины, Южный Крым | 0,67 | 0,57 | 1,82 |
Параметр расчётной продолжительности дождя
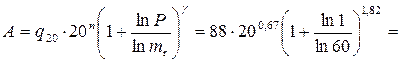 655 л/с/га =
655 л/с/га =
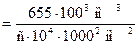 = 0,0655 мм/с = 3,93 мм/мин.
= 0,0655 мм/с = 3,93 мм/мин.
Из табл. 3.4 минимальная мгновенная стокообразующая интенсивность дождя, принимаемая равной интенсивности впитывания iст = U* =0,06 мм/мин. Продолжительность стокообразования
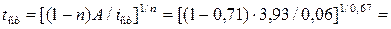 98,2 мин.
98,2 мин.
Таблица 3.4
| Грунты и почвы | Интенсивность впитывания U*, мм/мин |
| Глины, солонцы суглинистые | 0,06 |
| Суглинки, суглинистые черноземы, сероземы глинистые | 0,08 |
| Каштановые почвы, чернозем обычный, солонцы супесчаные | 0,15 |
| Супеси с примесью гумуса в верхних слоях, задернованные, супеси, серолесные почвы | 0,20 |
| Чистые открытые супеси | 0,33 |
| Чистые открытые пески | 0,50 |
Длина склона, участвующего в стоке сечения в точке B (равная пути движения воды за время стекания; с более удалённых участков вода не доходит, так как впитывается в грунт),
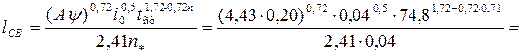 509 м.
509 м.
Из точек D и C вода приходит в точку B одновременно. Поскольку длина стока lDA определяется как путь движения воды за время 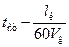 , то длина lDA оказывается зависимой от скорости течения воды по канаве Vк, которая в свою очередь зависит от геометрических размеров канавы и глубины потока
, то длина lDA оказывается зависимой от скорости течения воды по канаве Vк, которая в свою очередь зависит от геометрических размеров канавы и глубины потока 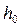 . Кроме того, от глубины потека
. Кроме того, от глубины потека 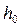 существенно зависит пропускная способность канавы Q0 которая в идеальном случае должна быть равна расчетному расходу Qр, зависящему от площади одновременного стока Fст, т.е. и от величины lDA. Поэтому величину lDA и связанную с ней глубину потока
существенно зависит пропускная способность канавы Q0 которая в идеальном случае должна быть равна расчетному расходу Qр, зависящему от площади одновременного стока Fст, т.е. и от величины lDA. Поэтому величину lDA и связанную с ней глубину потока 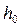 целесообразно определять методом подбора. Будем считать ширину канавы по дну величиной постоянной, равной b = 0,4 м, а глубину потока будем подбирать такой, чтобы пропускная способность канавы Q0 равнялась расчетному расходу Q.
целесообразно определять методом подбора. Будем считать ширину канавы по дну величиной постоянной, равной b = 0,4 м, а глубину потока будем подбирать такой, чтобы пропускная способность канавы Q0 равнялась расчетному расходу Q.
Скорость течения воды определяется по формуле
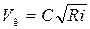 ,
,
где
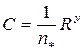 ;
; 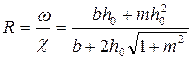 ;
; 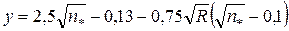 .
.
Результаты расчётов приведены в табл. 3.5.
Таблица 3.5
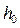 , м , м
| 0,40 | 0,50 | 0,424 |
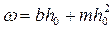 , м2 , м2
| 0,40 | 0,58 | 0,44 |
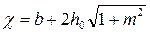 , м , м
| 1,84 | 2,20 | 1,93 |
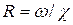 , м , м
| 0,22 | 0,26 | 0,23 |
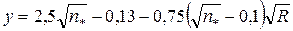
| 0,34 | 0,52 | 0,46 |
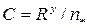 , м1/2/с , м1/2/с
| 15,0 | 16,0 | 15,2 |
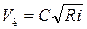 , м/с , м/с
| 0,44 | 0,52 | 0,46 |
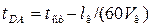 , мин , мин
| 52,9 | 59,5 | 54,7 |
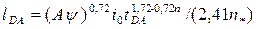 , м , м
| 47,4 | 54,8 | 49,4 |
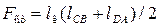 , га , га
| 33,4 | 33,8 | 33,5 |
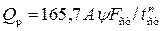 , л/с , л/с
| |||
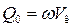 , л/с , л/с
|
Таким образом, расход Q = 202 л/с, глубина потока 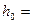 0,424 м, ширина канавы по дну b = 0,4 м, длина канавы lк = 1200 м; уклон канавы по дну i = 0,004; коэффициент заложения откосов m = 1,5, скорость потока в канаве Vк = 0,46 м/с.
0,424 м, ширина канавы по дну b = 0,4 м, длина канавы lк = 1200 м; уклон канавы по дну i = 0,004; коэффициент заложения откосов m = 1,5, скорость потока в канаве Vк = 0,46 м/с.
Полная глубина канавы с учётом превышения бровки канала над расчётным уровнем воды (рис. 3.3) hк = h0 + 0,25 = 0,42 + 0,25 ≈ 0,67 м.
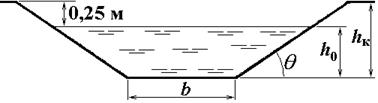
Рис. 3.3
Так как согласно табл. 3.6 допустимая скорость для глины составляет 1,2·0,85 = 1,02 м/с, что больше Vк = 0,46 м/с, то укрепления откосов и дна канавы не требуется.
Таблица 3.6
| Грунт лотка | Максимальная скорость, м/с | Вид укрепления откосов канав | Максимальная скорость, м/с |
| Мелкозернистый и среднезернистый песок, супеси | 0,4 | Одерновка плашмя | 1,0 |
| Одерновка в стенку | 1,6 | ||
| Крупнозернистый песок | 0,8 | Мощение одиночное | 2,0 |
| Суглинок | 0,7 | Мощение двойное | 3,5 |
| Суглинок тяжелый | 1,0 | Грунт, обработанный вяжущими | 5,0 |
| Глина | 1,2 | Бетонные плиты | 8,0 |
Примечание: Значения скоростей даны для глубины потока от 0,4 до 1,0 м. При глубине потока менее 0,4 м табличные значения скоростей принимаются с поправочным коэффициентом 0,85, а при глубине более 1 м – с коэффициентом 1,25.
4. Гидравлический расчёт нагорной канавы на сток талых вод
Величины исходных данных определяются по предпоследней y и последней z цифрам номера зачётной книжки.
Исходные данные: район Донецка; водосборная площадь F = (90 + 10y) га (задернованный суглинок). Озёра и болота отсутствуют, лес отсутствует Продольный уклон канавы i = 0,005 + z.
Решение. Максимальная интенсивность снеготаяния, определяемая по карте рис. 4.1, A = 1,3 мм/ч.
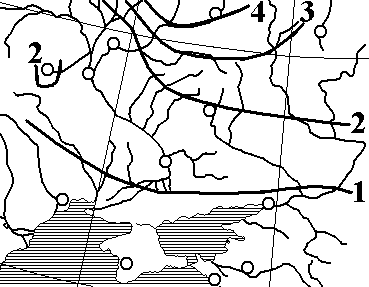
Рис. 4.1
С увеличением площади меняется интенсивность снеготаяния на отдельных участках бассейна, возрастает неодновременность добегания воды к расчётному створу со всей площади водосбора. Коэффициент редукции (уменьшения) максимального стока талых вод
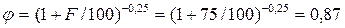 .
.
Коэффициент снижения расходов за счёт аккумуляции воды в болотах и озёрах на водосборе
δ' = 1 − 0,6∙lg(Fo + 0,2Fб + 1) = 1 − 0,6∙lg(0 + 0,2∙0 +1) = 1,
где Fo и Fб − доля в общей площади водосбора озёр и болот соответственно.
Коэффициент снижения расходов при наличии леса на водосборе
δ'' = 1 − γlg(1 + Fл) = 1 − 0,25∙lg(1 + 0) = 1,
где Fл − доля лесов в общей площади водосбора, γ – коэффициент, равный для лесов на песчаных и супесчаных почвах 0,35 – 0,40 и для лесов на суглинистых почвах – 0,25 – 0,30.
Расчётный расход талых вод, поступающих в канаву:
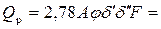 2,78·1,3∙0,87∙1,0∙1,0∙75 = 236 л/с,
2,78·1,3∙0,87∙1,0∙1,0∙75 = 236 л/с,
В расчётном сечении (в точке B рис. 3.1) задаёмся параметрами канавы: b = 0,4 м; коэффициент заложения откосов m = 1,5. Из табл. 3.1 коэффициент шероховатости грунтовой поверхности без дернового покрова 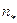 = 0,025. Решаем задачу методом подбора. Подбираем такое значение глубины потока в канаве, при котором расход воды в канаве равен расчётному расходу талых вод, поступающих в канаву. Площадь живого сечения
= 0,025. Решаем задачу методом подбора. Подбираем такое значение глубины потока в канаве, при котором расход воды в канаве равен расчётному расходу талых вод, поступающих в канаву. Площадь живого сечения 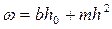 , смоченный периметр
, смоченный периметр 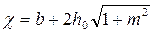 , гидравлический радиус
, гидравлический радиус 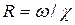 . Показатель степени
. Показатель степени 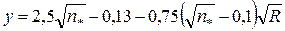 . Коэффициент Шези
. Коэффициент Шези 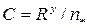 . Скорость воды в канаве
. Скорость воды в канаве 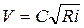 . Пропускная способность канавы в расчётном сечении
. Пропускная способность канавы в расчётном сечении 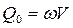 .
.
Результаты расчётов приведены в табл. 4.1.
Таблица 4.1
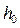 , м , м
| 0,30 | 0,40 | 0,346 |
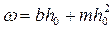 , м2 , м2
| 0,26 | 0,40 | 0,32 |
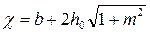 , м , м
| 1,48 | 1,84 | 1,65 |
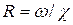 , м , м
| 0,17 | 0,22 | 0,19 |
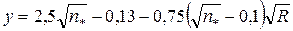
| 0,25 | 0,24 | 0,25 |
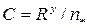 , м1/2/с , м1/2/с
| 25,9 | 27,5 | 26,7 |
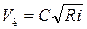 , м/с , м/с
| 0,68 | 0,81 | 0,74 |
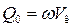 , л/с , л/с
|
Полная глубина канавы с учётом запаса глубины 0,25 м равна
hк = h0+ 0,25 = 0,35 + 0,25 = 0,60 м.
Так как согласно табл. 3.6 допустимая скорость для суглинка составляет 0,7·0,85 = 0,60 м/с, что меньше Vк = 0,74 м/с, то требуется укрепления откосов и дна канавы одерновкой плашмя. При этом максимально допустимая (неразмывающая) скорость движения воды возрастает до 1,0·0,85 = 0,85 м/с.
Дата добавления: 2016-02-04; просмотров: 1224;
