Уравнение Бернулли для потока реальной жидкости
При массовом расходе в живом сечении элементарной струйки . 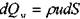 кинети-
кинети-
ческая энергия жидкости проходящей через это сечение в единицу времени будет равна:
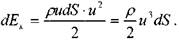
Суммируя величины кинетической энергии всех элементарных струек проходящих через живое сечение потока жидкости, найдём полную кинетическую энергию для всего
д
живого сечения потока
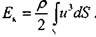
С другой стороны, полагая, что скорости во всех элементарных струйках одинаковы и равны средней скорости движения жидкости в живом сечении потока, таким же образом вычислим полную кинетическую энергию в этом же живом сечении потока. ' '
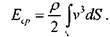
Вполне очевидно, что величины этих энергий не равны, т.е.
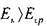
Тогда коэффициент, учитывающий неравномерность распределения скоростей по сечению (коэффициент Кориолиса) можно определить как соотношение кинетических энергий:
т? 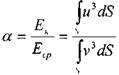
Внося эту поправку в уравнение для элементарной струйки жидкости, получим уравнение для потока конечных размеров. Практически а= 1.0- 2,0.
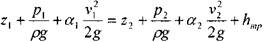
Кроме коэффициента Кориолиса, учитывающего неравномерность распределения кинетической энергии по живому сечкнию потока, существует аналогичный показатель для величины количества движения, коэффициент Буссинэ 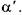
Секундное количество движения для потока жидкости можно определить как интегральную сумму количества движения элементарных масс жидкости, протекающих через бесконечно малые площадки ds в пределах площади всего живого сечения S, т.е.
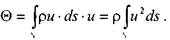
Аналогичным образом, величина количества движения жидкости в живом сечении при условии равномерного распределения сколостей по сечению потока будет:
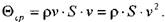
Отсюда коэффициент Буссинэ определится следующим образом:
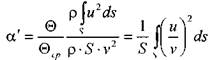
В связи с тем, что величина коэффициента количества движения (коэффициент Буссинэ) невелика и не превышает 1,05, поправкой в расчётах обычно пренебрегают,
Дата добавления: 2016-02-04; просмотров: 508;
