Экспериментальное изучение движения жидкости
При проведении многочисленных экспериментов с потоками движущейся жидкости было неоднократно подмечено, что на величину гидравлических сопротивлений кроме физических свойств самой жидкости, формы и размеров каналов, состояния их стенок, существенное влияние 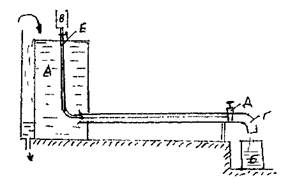 оказывает особенности движения частиц жидкости в потоке. Впервые дал теоретическое обоснование этой зависимости английский физик Осборн Рейнольде. Суть его эксперимента заключалась в следующем.
оказывает особенности движения частиц жидкости в потоке. Впервые дал теоретическое обоснование этой зависимости английский физик Осборн Рейнольде. Суть его эксперимента заключалась в следующем.
В ёмкость А достаточного большого объёма была вставлена длинная (не менее 20 диаметров) стеклянная трубка Г. На конце этой трубки устанавливался кран Д для регулирования расхода жидкости. Измерение расхода жидкости осуществлялось с помощью мерной ёмкости Б, расположенной в конце трубки. Из малого бачка В с помощью тонкой изогнутой трубки Е по центру основной трубки вводилась подкрашенная жидкость. Её расход также регулировался с помощью краника. Уровень жидкости в основном баке А поддерживался постоянным. Плавно меняя расход жидкости в трубке, Рейнольде отметил, что при малых скоростях движения жидкости подкрашенная струйка жидкости текла по центру потока жидкости, не смешиваясь с остальной жидкостью потока. Однако при определённой скорости жидкости подкрашенная струйка жидкости теряла свою устойчивость и, в конечном итоге, частицы окрашенной жидкости перемешивались с остальной жидкостью. При снижении скорости движения жидкости положение восстанавливалось: хаотичное движение частиц жидкости снова становилось упорядоченным. Рейнольде менял длину и диаметр трубки, вязкость жидкости, количество подкрашенных струек жидкости и установил, что эффект перемешивания (смена режима течения жидкости) зависит от скорости движения жидкости, её вязкости и от диаметра трубки, причём при увеличении вязкости жидкости для смены режима течения жидкости требовалась большая скорость. Отсюда Рейнольде сделал вывод, что смена режима движения жидкости зависит от целого комплекса параметров потока, а именно от соотношения:
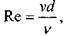
которое получило название числа Рейнольдса. Число Рейнольдса оказалось безразмерной величиной, представлявшей собой отношение сил инерции к силам вязкостного
трения. Была установлена и критическая величина числа Рейнольдса, при котором происходила смена режима движения жидкости R.eKp, она оказалась равной 2320.
Режим движения жидкости, при котором наблюдалось плавное, слоистое движение жидкости был назван ламинарным (слоистым) режимом движения жидкости. Режим движения жидкости сопровождавшийся хаотическим движением частиц жидкости в потоке был назван турбулентным (беспо 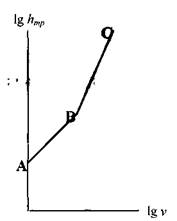 рядочным). Важным оказалось то обстоятельство, что при смене режима движения существенно менялась зависимость величины гидравлических сопротивлений от скорости движения жидкости. Этот факт можно проиллюстрировать на графике зависимости потерь напора от скорости, построенных в билогарифмической системе координат.
рядочным). Важным оказалось то обстоятельство, что при смене режима движения существенно менялась зависимость величины гидравлических сопротивлений от скорости движения жидкости. Этот факт можно проиллюстрировать на графике зависимости потерь напора от скорости, построенных в билогарифмической системе координат.
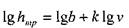
Зависимость состоит из двух участков: ламинарного (АВ) и турбулентного (ВС} режимов движения жидкости. Каждому из участков соответствует уравнение:
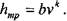
Для ламинарного участка (АВ) наклон линии к оси абсцисс k = tg45° = 1, для турбулентного участка (ВС) наклон линии превышает 1 и изменяется в пределах 1,75 - 2,0. 6.2. Ламинарное движение жидкости
Касательные напряжения. Рассмотрим правила определения величины касательных
напряжений на примере потока жидкости в круглой цилиндрической трубе. Двумя сечениями выделим в потоке жидкости отсек длиной /. На данный отсек жидкости будут действовать силы давления, приложенные к площадям жи 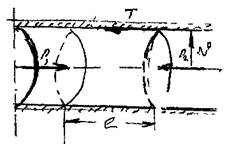 вых сечений потока жидкости слева и справа и сила трения, направленная в сторону обратную движению жидкости. Поскольку движение жидкости установившееся, то все действующие на отсек жидкости силы должны быть уравновешены. < • -
вых сечений потока жидкости слева и справа и сила трения, направленная в сторону обратную движению жидкости. Поскольку движение жидкости установившееся, то все действующие на отсек жидкости силы должны быть уравновешены. < • -
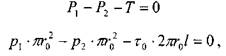
где: г0 - касательные напряжения на боковой поверхности отсека жидкости.
Касательные напряжения на периферии отсека жидкости (у стенки трубы) будут равны:
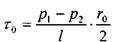
Очевидно, это будут максимальная величина касательных напряжений в отсеке жидкости. Вычислим величину касательных напряжений на расстоянии г от оси трубы.
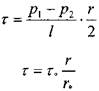
Таким образом, касательные напряжения по сечению трубы изменяются по линейному закону; в центре потока (на оси трубы) г=0 касательные напряжения т= 0.
Распределение скоростей в ламинарном потоке. Поскольку ламинарный поток жидкости в круглой цилиндрической трубе является осе симметричным, рассмотрим, как и ранее, лишь одно (вертикальное сечение трубы). Тогда, согласно гипотезе Ньютона:
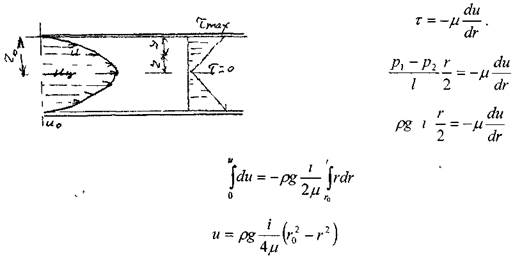
Отсюда видно, что распределение скоростей в круглой цилиндрической трубе соответствует параболическому закону. Максимальная величина скорости будет в центре трубы, где 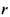 = О
= О
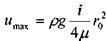
Средняя скорость движения жидкости в ламинарном потоке. Для определения величины средней скорости рассмотрим живое сечение потока жидкости в трубе Затем проведём в сечении потока две концентрические окружности, отстоящие друг от друга на бесконечно малое расстояние dr. Между этими окружностями мы, таким образом, выделили
малую кольцевую зону, малую часть живого сечения потока жидкости. Расход жидкости через выделенную кольцевую зону:
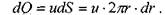
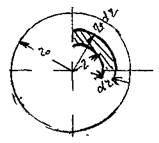 Расход жидкости
Расход жидкости  через полное живое сечение трубы:
через полное живое сечение трубы:
величина средней скорости в сечении:
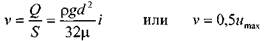
Потери напора в ламинарном потоке жидкости. Для ламинарного потока жидкости в круглой трубе можно определить коэффициент трения через число Рейнольдса. Вычислим величину гидравлического уклона из средней скорости жидкости.
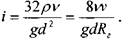
Отсюда:
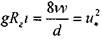
Тогда:
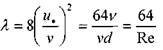
Окончательно потери напора при ламинарном движении жидкости в трубе:
j 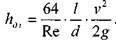
Несколько преобразовав формулу для определения потерь напора, получим формулу Пуазейля:
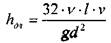
Дата добавления: 2016-02-04; просмотров: 645;
