Линии и трубки тока. Неразрывность струи

5.1 Линии и трубки тока

Гидродинамика – раздел физики жидкости, в котором изучается движение несжимаемых жидкостей и их взаимодействие с твёрдыми телами.

Существуют два метода описания движения жидкостей:

- метод Лагранжа, который связан с описанием каждой частицы жидкости с помощью функций времени;

- метод Эйлера, который связан с наблюдением отдельных точек пространства, заполненных жидкостью и фиксацией скорости прохождения через данные точки пространства отдельных частиц жидкости.

Состояние жидкости можно определить, указав для каждой точки пространства вектор скорости 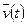. Совокупность этих векторов образуют поле вектора 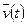. Касательная, проведённая из точек начала векторов и совпадающая с вектором, называется линией тока (рисунок 5.1).

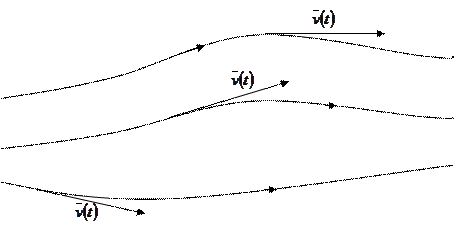
Рисунок 5.1 – Трубка тока с линиями тока

Количеством линий 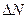, проходящих через площадку 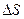, определяется густота линий тока. Будем считать, что густота линий тока пропорциональна величине скорости течения 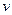, т.е. там, где скорость течения жидкости больше, там больше густота линий тока. При условии 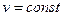течение называется установившемся или стационарным.

Часть жидкости, ограниченная линиями тока называется трубкой тока.

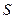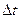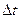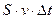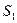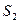Пусть через сечение течёт жидкость в течение времени . Тогда за время через данное сечение проходит объём жидкости равный . Если взять два разных сечения, имеющие площади и , будет наблюдаться следующее. Поскольку жидкость несжимаема и её плотность 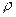постоянна во всех точках, то в единицу времени через оба сечения пройдёт одинаковое количество жидкости по объёму, т.е.

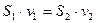. (5.1)

Таким образом, для несжимаемой жидкости выполняется условие:

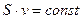. (5.2)

Выражение (5.2) является аналитической записью теоремы о неразрывности струи (рисунок 5.2).

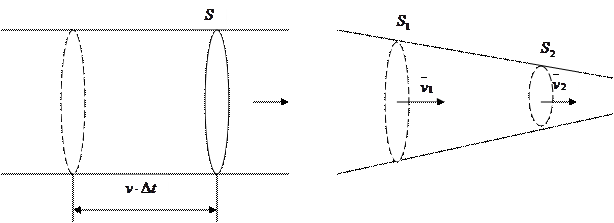а) б)

Рисунок 5.2 – Прохождение жидкости через а) сечение 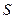за время 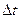; б) разные сечения 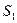и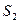

При изменении площади сечения 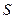частицы несжимаемой жидкости движутся с ускорением. Если взять трубку тока, то данное ускорение вызвано только непостоянством давления вдоль оси трубки. Там где скорость частиц меньше, давление должно быть больше и наоборот.

5.2 Уравнение Бернулли

Жидкость, в которой нет внутреннего трения, называется идеальной.

Рассмотрим трубку тока, изображенную на рисунке 5.3.

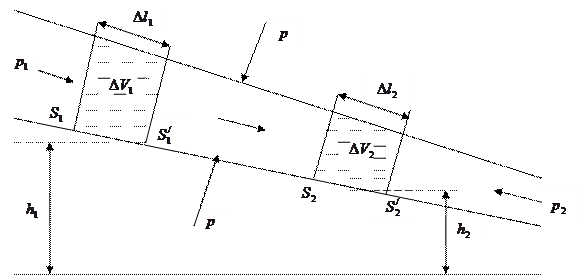Рисунок 5.3 – Трубка тока с разными поперечными сечениями

В силу неразрывности струи, заштрихованные объёмы 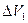и 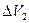будут равны 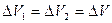. Если выполняются условия 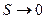и 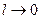, то выражение для приращения энергии струи будет иметь вид:

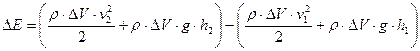. (5.3)

Приращение энергии 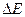должно быть равно только работе, совершаемой силами давления, т.к. трение отсутствует. Силы давления на боковую поверхность направлены перпендикулярно струе, поэтому их работа равна нулю. Работа сил давления, приложенных к сечениям 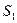и 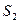, равна

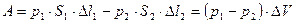. (5.4)

Приравниваем правые части выражений (5.3) и (5.4) и, сокращая на 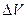, получаем

.

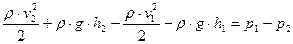После преобразований получаем окончательный вид выражения:

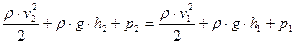. (5.5)

Таким образом, в стационарно текущей идеальной жидкости вдоль любой линии тока выполняется условие

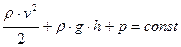. (5.6)

Выражение (5.6) является уравнением Бернулли.

Для горизонтальной линии тока, где выполняется условие 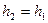, выражение (5.5) приобретает упрощённый вид

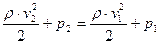, (5.7)

а уравнение Бернулли записывается:

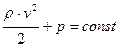. (5.8)

Таким образом, давление оказывается меньше там, где выше скорость течения.

5.3 Истечение жидкости из отверстия

В случае истечения жидкости из небольшого отверстия в широком открытом сосуде (рисунок 5.4) уравнение Бернулли запишется в следующем виде:

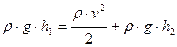. (5.9)

В выражении (5.9) величина 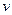означает скорость истечения жидкости из отверстия.

Пусть высота жидкости над отверстием определяется как

,

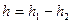тогда

.

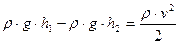Выразим скорость 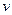, получим формулу Торричелли:

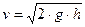. (5.10)

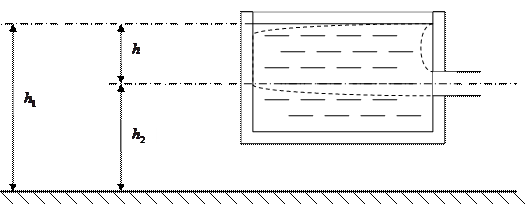Рисунок 5.4 – Истечение жидкости из отверстия в широком открытом сосуде

Как показано на рисунке 5.5, струя жидкости, вытекающая из отверстия в сосуде, уносит с собой за время 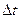импульс величиной

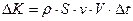, (5.11)

В выражении (5.11):

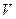- – скорость истечения струи из отверстия;

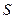- – площадь отверстия.

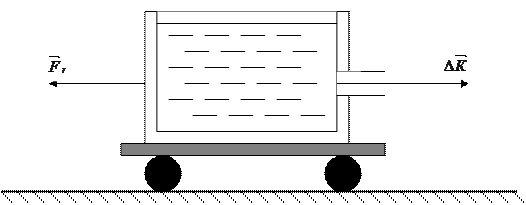Рисунок 5.5 – Реакция вытекающей струи

Тогда сила реакции вытекающей струи 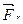определяется по формуле:

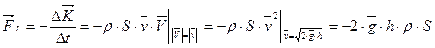. (5.12)

На реакции вытекающей струи основано реактивное движение.