Электрические свойства жидкостей
Вещества, в которых при прохождении через них электрического тока происходят химические реакции, называются электролитами или проводниками второго рода.
В качестве примеров можно привести:
- водные растворы солей;
- водные растворы кислот и щелочей;
- расплавы солей, которые в твёрдом состоянии являются ионными кристаллами.
Носители тока в электролитах – ионы, на которые расщепляются (диссоциируют) молекулы растворённого в воде вещества.
В растворе каждая молекула растворённого вещества находится в окружении молекул вещества растворителя. Поскольку молекулы растворителя и растворённого вещества являются полярными, то они распределяются в растворе как показано на рисунке 8.1.

Рисунок 8.1 – Взаимное расположение в растворе молекул растворителя и растворённого вещества.
Из-за ослабления связей между катионами и анионами, вызванного силами электрических взаимодействий, молекулы веществ могут диссоциировать. Иногда при встрече катиона и аниона молекулы исходного вещества снова соединяются – рекомбинируют. Таким образом, в растворе одновременно протекают два физических процесса:
- диссоциация молекул веществ;
- рекомбинация молекул веществ.
Если количество диссоциирующих молекул 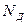 равно количеству рекомбинирующих
равно количеству рекомбинирующих 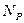 , то устанавливается равновесное состояние раствора. Этому состоянию характерна степень диссоциации, называемая коэффициентом диссоциации
, то устанавливается равновесное состояние раствора. Этому состоянию характерна степень диссоциации, называемая коэффициентом диссоциации 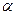 .
.
Пусть 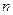 – это число молекул растворённого вещества в единице объёма раствора, тогда:
– это число молекул растворённого вещества в единице объёма раствора, тогда:
- 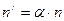 – число диссоциировавших молекул данного вещества в этой же единице объёма раствора;
– число диссоциировавших молекул данного вещества в этой же единице объёма раствора;
- 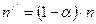 – оставшееся число молекул вещества.
– оставшееся число молекул вещества.
Таким образом, количество молекул растворённого вещества в единице объёма раствора определяется выражением 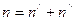 .
.
Пусть в единицу времени диссоциировало 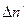 , а рекомбинировало
, а рекомбинировало 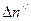 молекул растворённого вещества. Тогда:
молекул растворённого вещества. Тогда:
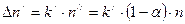 , (8.1)
, (8.1)
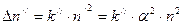 . (8.2)
. (8.2)
В выражениях (8.1), (8.2) коэффициенты 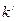 и
и 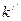 – это коэффициенты пропорциональности, зависящие от природы растворённого вещества и растворителя. При увеличении значения величины диэлектрической проницаемости растворителя
– это коэффициенты пропорциональности, зависящие от природы растворённого вещества и растворителя. При увеличении значения величины диэлектрической проницаемости растворителя 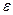 , значения коэффициентов пропорциональности
, значения коэффициентов пропорциональности 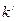 и
и 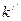 возрастают.
возрастают.
Известно, что в равновесном состоянии раствора обязательно выполнение условия 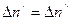 , а это значит, что и правые части выражений (8.1), (8.2) можно приравнять
, а это значит, что и правые части выражений (8.1), (8.2) можно приравнять
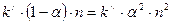 ,
,
или
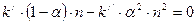 . (8.3)
. (8.3)
Если, раскрыв скобки, левую и правую части выражения (8.3) разделить на величину 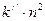 , то получится квадратное уравнение вида (8.4):
, то получится квадратное уравнение вида (8.4):
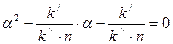 . (8.4)
. (8.4)
Квадратное уравнение (8.4) имеет два решения:
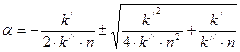 . (8.5)
. (8.5)
Поскольку, по определению, 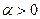 , вариант решения со знаком «–» не учитывается. Тогда второе слагаемое (8.5) преобразовывается к виду:
, вариант решения со знаком «–» не учитывается. Тогда второе слагаемое (8.5) преобразовывается к виду:
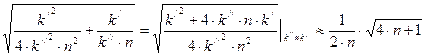 ,
,
а выражение (8.5) с учётом 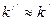 примет вид (8.6)
примет вид (8.6)
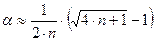 . (8.6)
. (8.6)
Из (8.6) следует, что при условии 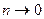 значение коэффициента
значение коэффициента 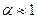 . Это говорит о том, что в слабых или сильноразбавленных растворах все молекулы растворённого вещества оказываются диссоциированными. При увеличении
. Это говорит о том, что в слабых или сильноразбавленных растворах все молекулы растворённого вещества оказываются диссоциированными. При увеличении 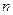 коэффициент
коэффициент 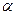 пропорционален отношению
пропорционален отношению 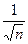 .
.
При невысоких температурах ионы бывают окружены молекулами растворителя (рисунок 8.2).
Рисунок 8.2 – Ион растворённого вещества, окружённый молекулами растворителя
Это явление носит название сольвация. Если раствор является водным, то явление носит название гидратация. При повышении температуры раствора размеры сольвата начинают уменьшаться.
Дата добавления: 2016-02-04; просмотров: 1946;
