Тормозное рентгеновское излучение. Фотоэффект. Формула Эйнштейна. Фотоны.

Тормозное рентгеновское излучение.

В предыдущей лекции мы говорили, что для объяснения свойств теплового излучения пришлось ввести представление об испу­скании электромагнитного излучения порциями ћw. Квантовая природа излучения подтверждается также рядом других явлений. Одним из них является существование так называемой коротко­волновой границы тормозного рентгеновского излучения.

Рентгеновские лучи возникают при бомбардировке Рис.3.11.1

быстрыми электрона­ми твердых мишеней.

Рентгеновская трубка (рис.3.11.1) представляет собой эвакуированный баллон с несколькими электродами. Нагревае­мый током катод K служит источником свободных электронов, испускаемых вследствие термоэлектронной эмиссии. Цилиндрический электрод Ц предназначен для фокусировки электронного пучка. Мишенью является анод A, который называют также антикатодом. Его делают из тяжелых металлов (W, Сu, Pt и т.д.). Ускорение электронов осуще­ствляется высоким напряжением, создаваемым между като­дом и антикатодом. Почти вся энергия электронов выделяется на антикатоде в виде тепла (в излучение превращается лишь 1—3 % энергии). Поэтому в мощных трубках антикатод прихо­дится интенсивно охлаждать. С этой целью в теле антикатода делаются каналы, по которым циркулирует охлаждающая жид­кость (вода или масло).

Если между катодом и антикатодом приложено напряжение U,электроны разгоняются до энергии eU. Попав в вещество антикатода, электроны испытывают сильное торможение и ста­новятся источником электромагнитных волн. Мощность излуче­ния Ρ пропорциональна квадрату заряда электрона е и квадрату его ускорения а: ~ .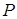

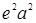Предположим, что ускорение электрона остается постоян­ным в течение всего времени торможения τ. Тогда мощность излучения также будет постоянной, и за время торможения электрон излучит энергию ~ ,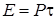

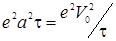где V₀ — начальная скорость электрона.

Полученный результат показывает, что заметное излучение может наблюдаться лишь при резком торможении быстрых электронов. На рентгеновские трубки подается напряжение до 50 кB. Пройдя такую разность потенциалов, электрон приобре­тает скорость, равную 0,4c (с – скорость света). Электроны могут быть ускорены также в бетатроне. В бетатроне электроны могут быть ускорены до энергии в 50 МэВ. Скорость электронов при такой энергии составляет 0,99995 с.Направив ускоренный в бетатроне пучок электронов на твердую мишень, получают рентгеновские лучи весьма малой длины волны. Чем меньше длина волны, тем меньше поглощаются лучи в веществе. Поэтому рентгеновские лучи, получаемые на бетатроне, обла­дают особенно большой проникающей способностью.

При достаточно большой скорости электронов, кроме тор­мозного излучения (т. е. излучения, обусловленного тор­можением электронов), возбуждается также характеристи­ческое излучение (вызванное возбуждением внутренних электронных оболочек атомов анти­катода). Сейчас нас будет ин­тересовать лишь тормозное излуче­ние. Согласно классической элек­тродинамике при торможении элек­трона должны возникать волны всех длин — от нуля до бесконечности. Длина волны, на которую прихо­дится максимум мощности излуче­ния, должна уменьшаться по мере увеличения скорости электронов, т. е. напряжения на трубке U. На рис.3.11.2 даны экспериментальные кривые распределения мощности тормозного рентгеновского излуче­ния по длинам волн, полученные для разных значений U. Как видно из Рис.3.11.2.

рисунка, выводы теории в основном подтверждаются на опыте.

Однако имеется одно принципиальное отступление от требований классической электродинамики. Оно заключается в том, что кривые распределения мощности не идут к началу коорди­нат, а обрываются при конечных значениях длины волны λ_min.

Экспериментально установлено, что коротковолновая граница тормозного рентгеновского спектра λ_min связана с ускоряющим напряжением U соотношением λ_min=12390/U, (3.11.1)

где λ_min выражена в ангстремах (1 ангстрем (Å) составляет 10 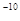м), a U — в вольтах.

Существование коротковолновой границы непосредственно вытекает из квантовой природы излучения. Действительно, если излучение возникает за счет энергии, теряемой электроном при торможении, то величина излученного кванта ħωне может превысить энер­гию электрона eU

ħω≤eU.

Отсюда получается, что частота излучения не может превысить значения ω_max=eU/ħ, аследовательно, длина волны не может быть меньше значения

λ_min =2πc /ω_max=(2πħ c/e)/U. (3.11.2)

Таким образом, мы пришли к эмпирическому соотношению (3.11.1). Найденное из сопоставления формул (3.11.1) и (3.11.2) значе­ние ħ хорошо согласуется со значениями, определенными иными способами. Из всех методов определения ħ метод, основанный на измерении коротковолновой границы тормозного рентгенов­ского спектра, считается самым точным.

Фотоэффект. Формула Эйнштейна.

Фотоэлектрическим эффектом или фотоэффектом назы­вается испускание электронов веществом под действием света. Это явление было открыто Г. Герцем в 1887 г. Он заметил, что проскакивание искры между шариками разрядника значительно облегчается, если один из шариков осветить ультрафиолетовыми лучами.

В 1888—1889 гг. А. Г. Столетов подверг фотоэффект систе­матическому исследованию с помощью установки, схема кото­рой показана на рис.3.11.3. Конденсатор, образованный проволоч­ной сеткой и сплошной пластиной, был включен последовательно с гальванометром G в цепь батареи. Свет, проходя через сетку, падал на сплошную пластину. В результате в цепи возникал ток, регистрировавшийся гальванометром. На основании своих опы­тов Столетов пришел к следующим выводам:

1) наибольшее действие оказывают ультрафиолетовые лучи; Рис.3.11.3.

2) сила тока воз­растает с увеличением освещенности пластины;

3) испускаемые под действием света заряды имеют отрицательный знак.

Спустя 10 лет (в 1898 г,) Ленард и Томсон, измерив удель­ный заряд испускаемых под действием света частиц, установили, что эти частицы являются электронами.

Ленард и другие исследователи усовершенствовали прибор Столетова, поместив электроды в эвакуированный баллон (рис3.11.4). Свет, проникающий через кварцевое окошко Кв, освещает катод К, изготовленный из исследуемого материала. Электроны, испущенные вследствие фотоэффекта, перемещаются под действием электрического поля к аноду А. Рис.3.11.4.

В результате в цепи прибора течет фототок, измеряемый

гальванометром G. На­пряжение между анодом и катодом можно изменять с помощью потенциометра П.

Полученная на таком приборе вольтамперная характери­стика (т. е. кривая зависимости фототока I от напряжения между электродами U)приведена на рис.3.11.5. Естественно, что характеристика снимается при неизменном потоке света Ф. Из этой кривой видно, что при некотором не очень большом напряжении фототок достигает насыщения — все электроны, испущен­ные катодом, попадают на анод.

Рис.3.11.5.

Следовательно, сила тока на­сыщения I_н определяется количеством электронов, испускаемых катодом в единицу времени под действием света.

Пологий ход кривой указывает на то, что электроны выле­тают из катода сразличными по величине скоростями. Доля электронов, отвечающая силе тока при U = 0, обладает скоро­стями, достаточными для того, чтобы долететь до анода «само­стоятельно», без помощи ускоряющего поля. Для обращения силы тока в нуль нужно приложить задерживающее напряжение U₃ (потенциал катода выше потенциала анода). При таком напряжении ни одному из элек­тронов, даже обладающему при вылете из катода наибольшим значением скорости V_m, не удается преодолеть задерживающее поле и достигнуть анода. Поэтому можно написать, что

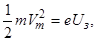(3.11.3)

где m – масса электрона. Таким образом, измерив задерживающее напряжение U_з, можно определить максимальное значение скорости фотоэлектронов.

К 1905 г. было выяснено, что максимальная скорость фото­электронов не зависит от интенсивности света, а зависит только от его частоты — увеличение частоты приводит к возрастанию скорости. Установленные экспериментально зависимости не укладываются в рамки классических представлений. Например,

1.скорость фотоэлектронов по классическим понятиям должна воз­растать с амплитудой, а, следовательно, и с интенсивностью электромагнитной волны;

2.максимальное значение скорости должно наблюдаться при некотором значении частоты 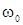; уменьшение или увеличение частоты подаваемого излучения должно приводить к уменьшению скорости электронов.

В 1905 г. А. Эйнштейн показал, что все закономерности фото­эффекта легко объясняются, если предположить, что свет погло­щается такими же порциями ћω (квантами), какими он, по пред­положению Планка, испускается. По мысли Эйнштейна, энер­гия, полученная электроном, доставляется ему в виде кванта ћω, который усваивается им целиком. Часть этой энергии, рав­ная работе выхода A, затрачивается на то, чтобы электрон мог покинуть тело (энергия электрона в веществе меньше его энергии снаружи). Если электрон освобождается светом не у самой поверхности, а на некоторой глубине, то часть энергии, равная E’, может быть потеряна вследствие случайных столк­новений в веществе. Остаток энергии образует кинетическую энергию E_к электрона, покинувшего вещество. Энергия E_к бу­дет максимальна, если E’ = 0. В этом случае должно выпол­няться соотношение

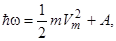(3.11.4)

которое называется формулой Эйнштейна для фотоэффекта .

Фотоэффект и работа выхода в сильной степени зависят от состояния поверхности металла (в частности, от находящихся на ней окислов и адсорбированных веществ). Поэтому долгое время не удавалось проверить формулу Эйнштейна с достаточ­ной точностью. В 1916 г. Милликен создал прибор, в котором исследуемые поверхности подвергались очистке в вакууме, после чего измерялась работа выхода и исследовалась зависимость максимальной кинетической энергии фотоэлектронов от частоты света (эта энергия определялась путем измерения задерживаю­щего потенциала U_З). Результаты оказались в полном согласии с формулой (3.11.4).

Подставив в формулу (3.11.4) измеренные значения A и ½mV_m² (при данной ω), Милликен определил значение постоянной Планка ћ, которое оказалось совпадающим со значениями, най­денными из спектрального распределения равновесного тепло­вого излучения и из коротковолновой границы тормозного рент­геновского спектра.

Из формулы (3.11.4) вытекает, что в случае, когда работа выхода А превышает энергию кванта ћω, электроны не могут покинуть металл. Следовательно, для возникновения фотоэф­фекта необходимо выполнение условия ћω≥ A, или

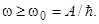(3.11.5)

Соответственно для длины волны получается условие:

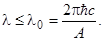(3.11.6)

Частота ω₀ или длина волны λο называется красной грани­цей фотоэффекта.

Число высвобождаемых вследствие фотоэффекта электронов должно быть пропорционально числу падающих на поверхность квантов света. Вместе с тем световой поток Φ определяется ко­личеством квантов света, падающих на поверхность в единицу времени. В соответствии с этим ток насыщения I_н должен быть пропорционален падающему световому потоку:

I_н ~ Ф.

Эта зависимость также подтверждается экспериментально. За­метим, что лишь малая часть квантов передает свою энергию фотоэлектронам. Энергия остальных квантов затрачивается на нагревание вещества, поглощающего свет.

В рассмотренном выше явлении фотоэффекта электрон полу­чает энергию от одного лишь фотона.

Кроме рассмотренного нами в внешнего фотоэффекта (называемого обычно просто фотоэффектом), существует также внутренний фотоэффект, наблюдае­мый в диэлектриках и полупроводниках. В этих веществах отсутствуют свободные электроны. Поэтому электрону, чтобы покинуть вещество, необходимо затратить больше энергии. Кроме работы выхода из вещества 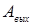ему нужно еще совершить работу для отрыва от атома 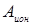. Поэтому, если энергия фотона 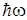лежит в интервале 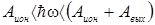, то в веществе образуется большое количество свободных электронов. Этот эффект используется в ряде приборов, получивших разнообразное применение в науке и технике. В частности, в применяемых для питания аппаратуры солнечных батареях.

Фотоны.

Чтобы объяснить распределение энергии в спектре равновес­ного теплового излучения, достаточно, как показал Планк, до­пустить, что свет только испускается порциями ћω. Для объяс­нения фотоэффекта достаточно предположить, что свет погло­щается такими же порциями. Однако Эйнштейн пошел значи­тельно дальше. Он выдвинул гипотезу, что свет и распростра­няется в виде дискретных частиц, названных первоначально световыми квантами. Впослед­ствии эти частицы получили название фотонов.

Наиболее непосредственное под­тверждение гипотезы Эйнштейна дал опыт Боте. Тонкая металлическая фольга Φ (рис.3.11.6) помещалась между двумя газоразрядными счетчи­ками Сч. Фольга освещалась слабым пучком рентгенов­ских лучей, под действием которых она сама становилась источником рентгеновских лучей (это явление на­зывается рентгеновской флуо­ресценцией). Вследствие малой интенсивности первичного пучка количество квантов, испускае­мых фольгой, было невелико. При попадании в него рентгеновских лучей счетчик срабатывал и приводил в действие особый механизм М, делавший отметку на Рис.3.11.6.

движущейся ленте Л. Если бы излучаемая энергия

распространялась равномерно во все стороны, как это следует из волновых представлений, оба счетчика должны были бы срабатывать одновременно и отметки на ленте приходились бы одна против другой. В действитель­ности же наблюдалось совершенно беспорядочное расположение отметок. Это можно объяснить лишь тем, что в отдельных актах испускания возникают световые частицы, летящие то в одном, то в другом направлении.

Итак, было экспериментально доказано существование осо­бых световых частиц – фотонов. Энергия фотона опреде­ляется его частотой:

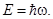(3.11.7)

Электромагнитная волна обладает импульсом. Соответственно должен обладать импульсом и фо­тон. Чтобы определить импульс фотона, воспользуемся соотно­шениями теории относительности. Рассмотрим две системы от­счета К. и К.', движущиеся друг относительно друга со скоростью V 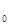. Оси x и x' направим вдоль V₀. Пусть в направлении этих осей летит фотон. Энергия фотона в системах К и К’ равна соответ­ственно ћω и ћω’, Частоты ω и ω' связаны соотношением

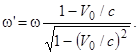
Следовательно,

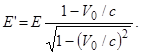(3.11.8)

Обозначим импульс фотона в системе К символом 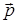, в систе­ме К' — символом 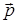'. Из соображений симметрии следует, что импульс фотона должен быть направлен вдоль оси x. Поэтому р_х = p, p_x’=p'· При переходе от одной системы отсчета к дру­гой энергия и импульс преобразуются по формуле

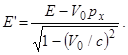(3.11.9)

В рассматриваемом нами случае можно заменить в (3.11.9) р_x через р.

Из сопоставления формул (3.11.9) и (3.11.8) следует, что

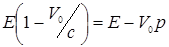
(мы написали p вместо р_x)· Отсюда

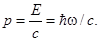(3.11.10)

Такое соотношение между импульсом и энергией возможно только для частиц с нулевой массой покоя, движущихся со скоростью с. Таким образом, из квантового соотношения Ε = ћωи общих принципов теории относительности вытекает, что

1) масса покоя фотона равна нулю,

2) фотон всегда движется со скоростью с.

Сказанное означает, что фотон представляет собой частицу особого рода, отличную от таких частиц, как электрон, протон и т. п., которые могут существовать, двигаясь со скоростями, меньшими c, и даже покоясь.

Заменив в формуле (3.11.10) частоту ω через длину волны λ, получим для импульса фотона выражение

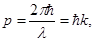(3.11.11)

(k — волновое число). Фотон летит в направлении распростране­ния электромагнитной волны. Поэтому направления импульса p и волнового вектора k совпадают. Следовательно, формулу (3.11.11) можно написать в векторном виде:

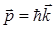. (3.11.12)

Пусть на поглощающую свет поверхность падает поток фото­нов, летящих по нормали к поверхности. Если плотность фото­нов равна n, на единицу поверхности падает в единицу времени nc фотонов. При поглощении каждый фотон сообщает стенке импульс p = Ε/с. Умножив p на nc, получим импульс, сооб­щаемый в единицу времени единице поверхности, т. е. давление P света на стенку:

P=(E/c)nc=En.

Произведение En равно энергии фотонов, заключенных в еди­нице объема, т.е. плотности электромагнитной энергии w. Таким образом, мы пришли к формуле P=w, которая совпадает с выражением для давления, получающимся из электромагнитной теории. Отражаясь от стенки, фотон сообщает ей импульс 2р. Поэтому для отражающей по­верхности давление будет равно 2w.

В данной лекции мы рассмотрели ряд явлений, в которых свет ведет себя как поток частиц (фотонов). Однако не надо забы­вать, что такие явления, как интерференция и дифракция света, могут быть объяснены только на основе волновых представле­ний. Таким образом, свет обнаруживает корпускулярно-волновой дуализм (двойственность): в одних явлениях проявляется его волновая природа, и он ведет себя как электро­магнитная волна, в других явлениях проявляется корпускуляр­ная природа света, и он ведет себя как поток фотонов. В дальнейшем мы увидим, что корпускулярно-волновой дуализм присущ не только световым частицам, но и частицам вещества (электро­нам, протонам, атомам и т. д.).

Лекция 3.12