Дифракционная решетка как спектральный прибор.

Дифракционная решетка является важнейшим спектральным прибором, предназначенным для разложения света в спектр и измерения длин волн. Из формулы (3.9.4), определяющей направления на главные фраунгоферовы максимумы, видно, что эти направления 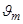зависят от длины световой волны l (за исключением максимума нулевого порядка, m = 0). Поэтому решетка в каждом порядке m ¹ 0 разложит падающий на нее свет в спектр различных порядков. Причем наибольшее отклонение в каждом порядке испытывает красная часть спектра (более длинноволновая).

Основными характеристиками любого спектрального прибора являются угловая дисперсия, разрешающая способность и область дисперсии.

1.Угловая дисперсия D характеризует степень пространственного (углового) разделения волн с различными длинами l. По определению,

(3.9.10)

где 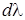- разность длин волн, дающих максимум данного порядка, - разность углов под которыми эти максимумы наблюдаются.

Дифференцируя формулу (3.9.4) при данном m находим для решетки 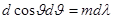, откуда

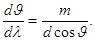(3.9.11)

Видно, что для заданного порядка m спектра угловая дисперсия тем больше, чем меньше период d решетки. Кроме того, 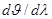растет с увеличением угла дифракции .

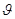2. Разрешающая способность R. По определению,

(3.9.12)

где 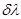— наименьшая разность длин волн спектральных линий, при которой эти линии воспринимаются еще раздельно, т. е. разрешаются. Величина R не может быть по ряду причин определена точно, а лишь ориентировочно (условно). Такой условный критерий был предложен Рэлеем.

Согласно критерию Рэлея, спектральные линии с разными длинами волн, но одинаковой интенсивности, Рис.3.9.8.

считаются разрешенными, если главный максимум одной спектральной линии совпадает с первым минимумом другой (рис.3.9.8). В этом случае между двумя максимумами возникает провал, составляющий около 20% от интенсивности в максимумах, и линии еще воспринимаются раздельно.

Итак, согласно критерию Рэлея и формуле (3.9.9), необходимо, чтобы максимум m-го порядка (m’ = mN) линии с длиной волны l + dl (рис.3.9.8) совпадал по направлению с первым минимумом линии l (m’ = mN + 1), т. е.

Отсюда следует, что

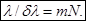(3.9.13)

Это и есть искомая формула для разрешающей способности дифракционной решетки. Данная формула дает верхний предел разрешающей способности. Она справедлива при выполнении следующих условий:

1. Интенсивность обоих максимумов должна быть одинаковой.

2. Расширение линий должно быть обусловлено только дифракцией.

3. Необходимо, чтобы падающий на решетку свет имел ширину когерентности, превышающую размер решетки. Только в этом случае все N штрихов решетки будут “работать” согласованно (когерентно), и мы достигнем желаемого результата.

Для повышения разрешающей способности спектральных приборов можно, как показывает формула (3.9.13), либо увеличивать число N когерентных пучков, либо повышать порядок интерференции m. Первое используется в дифракционных решетках (число N доходит до 200 000), второе — в интерференционных спектральных приборах (например, в интерферометре Фабри—Перо число N интерферирующих волн невелико, порядка нескольких десятков, а порядки интерференции m ~ 10⁶ и более).

3. Область дисперсииDl — это ширина спектрального интервала, при которой еще нет перекрытия спектров соседних порядков. Если спектры соседних порядков перекрываются, то спектральный аппарат становится непригодным для исследования соответствующего участка спектра.

Длинноволновый конец спектра m-го порядка совпадает с коротковолновым концом спектра (m + 1)-го порядка, если m(l + Dl) = (m + 1) l, откуда следует, что область дисперсии

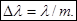(3.9.14)

Значит, область дисперсии Dl обратно пропорциональна порядку спектра т. При работе со спектрами низких порядков (обычно второго или третьего) дифракционная решетка пригодна для исследования излучения, занимающего достаточно широкий спектральный интервал.

Дифракция на двумерных и трехмерных решетках.

Двумерной решеткой называется структура, свойства которой периодически меняются в двух направлениях. Примером могут служить две скрещенные одномерные решетки, т.е. наложенные одна на другую под некоторым углом. Дифракционная картина от такой структуры может быть получена путем наложения дифракционных картин от соответствующих одномерных решеток.

Трехмерные, пространственные решетки обладают периодичностью в трех различных направлениях. Они играют важную роль в физике рентгеновских лучей. Дифракцию рентгеновских лучей на оптических дифракционных решетках получить нельзя, так как длина волны рентгеновского излучения имеет порядок 0,1нм, т.е. значительно меньше ширины щели оптической решетки. Дифракцию рентгеновских лучей можно наблюдать, если использовать кристаллическую структуру, как естественную периодическую пространственную решетку. В этом случае картина получается весьма сложной. Однако, ее можно использовать как для изучения спектрального состава излучения (если известны параметры кристалла), так и для определения характеристик кристалла (если известна длина волны излучения.

Голография.

Голография (от греческого холос – полный, графо – пишу) – способ получения объемных изображений предметов на фотопластинке при помощи когерентного излучения.

При освещении предмета от него распространяется рассеянная волна. Эта волна несет полную информацию о форме и других свойствах предмета. Попадая в глаз или объектив фотоаппарата, она образует на сетчатке или фотопластинке изображение. По степени почернения фотопластинки можно судить об амплитуде рассеянной волны. Таким образом, пластинка в этом случае сохраняет информацию только об амплитуде волны. Мы получаем плоское изображение. Для восстановления волнового поля в полном объеме (объемного изображения) этой информации недостаточно. Нужна еще информация о фазе, которую пластинка не содержит.

В 1947году английский физик и инженер Д.Габор показал, что необходимую информацию о фазе можно получить и записать на той же фотопластинке, если осветить ее вторым пучком от того же когерентного источника и заставить его интерферировать с пучком, рассеянным предметом.

Голограмма фиксирует не само изображение предмета, а структуру отраженной от него световой волны (амплитуду и фазу). Для получения голограммы необходимо, чтобы на фотопластинку одновременно попали два когерентных световых пучка: предметный, отраженный от снимаемого объекта, и опорный – приходящий непосредственно от источника. Свет обоих пучков интерферирует, создавая на пластинке чередование темных и светлых интерференционных полос. Рис.3.9.9.

Принципиальная схема устройства для записи голограммы приведена на рис.3.9.9. В этой схеме луч лазера делится специальным устройством на два. После этого лучи с помощью линз расширяются и с помощью зеркал направляются на объект и фотопластинку. Свет обоих пучков интерферирует, создавая на пластинке чередование темных и светлых полос. На экспонированной таким образом и проявленной пластинке отсутствует какое-либо изображение. Однако его в зашифрованном виде содержит система интерференционных полос. Если голограмму просветить, как диапозитив, лазерным светом той же частоты, что была использована при записи, возникнет «восстановленная голограмма» - объемное изображение предмета, словно висящее в пространстве. Меняя точку наблюдения, можно заглянуть за предметы на первом плане и увидеть детали, ранее скрытые от взгляда. Свет, проходя сквозь систему полос голограммы, дифрагирует и воспроизводит волновой фронт, исходивший от снятого предмета. Аналогичным образом лазерный луч, пропущенный через маленькое отверстие, дает на фотопластинке, поставленной за отверстием систему колец (дифракция Френеля). А световой пучок, проходящий сквозь такую пластинку, сойдется в точку. Таким образом, система колец, полученная при дифракции Френеля представляет собой простейшую голограмму – голограмму точки.

ЭЛЕМЕНТЫ КВАНТОВОЙ ФИЗИКИ.

Лекция 3.10.

Тепловое излучение. Формула Планка.

Тепловое излучение и люминесценция

Излучение телами электромагнитных волн (свечение тел) может осуществляться за счет различных видов энергии. Самым распространенным является тепловое излучение, т. е. испускание электромагнитных волн за счет внутренней энергии тел. Все остальные виды свечения, возбуждаемые за счет любого вида энергии, кроме внутренней (тепловой), объединяются под общим названием «люминесценция».

Окисляющийся на воздухе фосфор светится за счет энергии, выделяемой при химическом превращении. Такой вид свечения называется хемилюминесценцией. Свечение, возникающее в газах и твердых телах под воздействием электрического поля, называется электролюминесценцией. Свечение твердых тел, вызванное бомбардировкой их электронами, называют катодолюминесценцией. Свечение, возбуждаемое поглощаемым телом электромагнитным излучением, называется фотолюминесценцией.

Тепловое излучение имеет место при любой температуре, однако при невысоких температурах излучаются практически лишь длинные (инфракрасные) электромагнитные волны.

Окружим излучающее тело оболочкой с идеально отражающей поверхностью (рис. 3.10.1). Воздух из оболочки удалим. Отраженное оболочкой излучение, упав на тело, поглотится им (частично или полностью). Следовательно, будет происходить непрерывный обмен энергией между телом и заполняющим оболочку излучением. Если распределение энергии между телом и излучением остается неизменным для каждой длины волны, состояние системы тело — излучение будет равновесным. Опыт показывает, что единственным видом излучения, которое может находиться Рис.3.10.1.

в равновесии с излучающими телами, является тепловое

излучение. Все остальные виды излучения оказываются неравновесными.

Способность теплового излучения находиться в равновесии с излучающими телами обусловлена тем, что его интенсивность возрастает при повышении температуры. Допустим, что равновесие между телом и излучением нарушено и тело излучает энергии больше, чем поглощает. Тогда внутренняя энергия тела будет убывать, что приведет к понижению температуры. Это в свою очередь обусловит уменьшение количества излучаемой телом энергии. Температура тела будет понижаться до тех пор, пока количество излучаемой телом энергии не станет равным количеству поглощаемой энергии. Если равновесие нарушится в другую сторону, т. е. количество излучаемой энергии окажется меньше, чем поглощаемой, температура тела будет возрастать до тех пор, пока снова не установится равновесие. Таким образом, нарушение равновесия в системе тело — излучение вызывает возникновение процессов, восстанавливающих равновесие.

Иначе обстоит дело в случае люминесценции. Покажем это на примере хемилюминесценции. Пока протекает обусловливающая излучение химическая реакция, излучающее тело все больше и больше удаляется от первоначального состояния. Поглощение телом излучения не изменит направления реакции, а наоборот, приведет к более быстрому (вследствие нагревания) протеканию реакции в первоначальном направлении. Равновесие установится лишь тогда, когда будет израсходован весь запас реагирующих веществ и свечение, обусловленное химическими процессами, заменится тепловым излучением.

Итак, из всех видов излучения равновесным может быть только тепловое излучение. К равновесным состояниям и процессам применимы законы термодинамики. Поэтому тепловое излучение должно подчиняться некоторым общим закономерностям, вытекающим из принципов термодинамики. К рассмотрению этих закономерностей мы и перейдем.

Характеристики излучения и излучающего тела.

Обозначим через u плотность энергии излучения, т.е. количество энергии в единице объема. Излучение представляет собой совокупность волн различных частот (бегущих или стоячих). Поскольку плотность энергии излучения разной частоты различна, обозначим объемную плотность лучистой энергии, приходящийся на интервал частот . Очевидно, что

. (3.10.1)

Интенсивность теплового излучения мы будем характеризовать величиной потока энергии, измеряемой в ваттах. Энергия излучения связана с излучающим телом. Поток энергии, испускаемый единицей поверхности излучающего тела по всем направлениям (в пределах телесного угла 2π), называют энергетической светимостью тела. Мы будем обозначать эту величину буквой R. Энергетическая светимость является функцией температуры.

Излучение состоит из волн различных частот ω (или длин 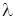). Обозначим поток энергии, испускаемый единицей поверхности тела в интервале частот dω, через dR_ω. При малом интервале dω поток dR_ω будет пропорционален dω:

. (3.10.2)

Величина r_ω называется испускательной способностью тела. Как и энергетическая светимость, испускательная способность сильно зависит от температуры тела. Таким образом, r_ω есть функция частоты и температуры. Испускательная способность это поток энергии, излучаемый единицей поверхности тела во всех направлениях в единичном интервале частот вблизи .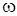

Энергетическая светимость связана с испускательной способностью формулой

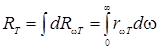(3.10.3)

(чтобы подчеркнуть, что энергетическая светимость и испускательная способность зависят от температуры, мы их снабдили индексом Т).

Излучение можно характеризовать вместо частоты ω длиной волны. Участку спектра dω будет соответствовать интервал длин волн dλ. Определяющие один и тот же участок величины dω и dλ связаны простым соотношением, вытекающим из формулы λ=2πc/ω. Дифференцирование дает:

. (3.10.4)

Знак минус в этом выражении не имеет существенного значения, он лишь указывает на то, что с возрастанием одной из величин, ω или λ, другая величина убывает. Поэтому минус в дальнейшем мы не будем писать.

Доля энергетической светимости, приходящаяся на интервал dλ, может быть по аналогии с (3.10.2) представлена в виде:

. (3.10.5)

Если интервалы dω и dλ, входящие в выражения (3.10.2) и (3.10.5), связаны соотношением (3.10.4), т. е. относятся к одному и тому же участку спектра, то величины dR_ω и dR_λ должны совпадать:

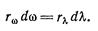
Заменив в последнем равенстве dλ согласно (3.10.4), получим

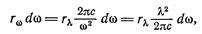
откуда

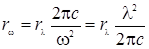. (3.10.6)

С помощью формулы (3.10.6) можно перейти от r_λ к r_ω и наоборот.

Пусть на элементарную площадку поверхности тела падает поток лучистой энергии dФ_ω, обусловленный электромагнитными волнами, частота которых заключена в интервале dω. Часть этого потока dФ’_ω будет поглощена телом, Безразмерная величина

(3.10.7)

называется поглощательной способностью тела. Поглощательная способность тела есть функция частоты и температуры. Поглощательная способность это доля энергии, поглощенная телом из падающего на него потока.

По определению a_ωT не может быть больше единицы. Для тела, полностью поглощающего упавшее на него излучение всех частот, a_ωT = 1. Такое тело называется абсолютно черным. Будем в дальнейшем обозначать испускательную и поглощательную способность абсолютно черного тела и . Тело, для которого a_ωT ≡ a_T =const<1, называют серым. Если 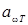= 0, это или абсолютно прозрачное тело или абсолютно зеркальное.

Закон Кирхгофа.

Между испускательной и поглощательной способностями любого тела имеется связь. В этом можно убедиться, рассмотрев следующий эксперимент. Пусть внутри замкнутой оболочки, поддерживаемой при постоянной температуре Т, помещены несколько тел (рис.3.10.2). Полость внутри оболочки эвакуирована

(там отсутствуют молекулы какого-либо вещества), так что тела могут обмениваться энергией между собой и с оболочкой лишь путем испускания и поглощения электромагнитных волн. Опыт показывает, что такая система через некоторое время придет в состояние теплового равновесия — все тела примут одну и ту же температуру, равную температуре оболочки Т. В Рис.3.10.2.

таком состоянии тело, обладающее бóльшей испускательной

способностью r_ωT, теряет в единицу времени с единицы поверхности больше энергии, чем тело, обладающее меньшей r_ωT. Поскольку температура (а, следовательно, и энергия) тел не меняется, то тело, испускающее больше энергии, должно и больше поглощать, т. е. обладать большей a_ωT. Таким образом, чем больше испускательная способность тела r_ωT, тем больше и его поглощательная способность a_ωT. Отсюда вытекает соотношение

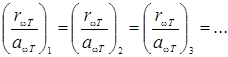, (3.10.8)

где индексы 1, 2, 3 и т. д. относятся к разным телам.

Соотношение (3.10.8) выражает установленный Кирхгофом закон, который формулируется следующим образом: отношение испускательной и поглощательной способностей не зависит от природы тела, оно является для всех тел одной и той же (универсальной) функцией частоты (длины волны) и температуры:

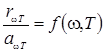. (3.10.9)

Сами величины r_ωT и a_ωT могут меняться чрезвычайно сильно при переходе от одного тела к другому. Отношение же их оказывается одинаковым для всех тел. Это означает, что тело, сильнее поглощающее какие-либо лучи, будет эти лучи сильнее и испускать (не следует смешивать испускание лучей с их отражением). Функция называется функцией Кирхгофа.

Для абсолютно черного тела по определению a_ωT = 1. Следовательно, из формулы (3.10.9) вытекает, что r_ωT для такого тела равна f(ω, Т). Таким образом, универсальная функция Кирхгофа f(ω, Т) есть не что иное, как испускательная способность абсолютно черного тела

При теоретических исследованиях для характеристики спектрального состава равновесного теплового излучения удобнее пользоваться функцией частоты f(ω,Т). В экспериментальных работах удобнее пользоваться функцией длины волны φ(λ, Т). Обе функции связаны друг с другом формулой

(3.10.10)

аналогичной формуле (3.10.6). Согласно (3.10.10) для того, чтобы по известной функции f(ω, Т) найти φ(λ, Т), нужно заменить в f(ω, Т) частоту ω через 2πс/λ и получившееся выражение умножить на 2πс/λ²:

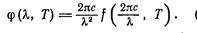(3.10.11)

Для нахождения f(ω, Т) по известной φ(λ, Т) нужно воспользоваться соотношением

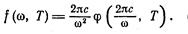(3.10.12)

Абсолютно черных тел в природе не существует. Сажа или платиновая чернь имеют поглощательную способность a_ωT, близкую к единице, лишь в ограниченном интервале частот; в далекой инфракрасной области их поглощательная способность заметно меньше единицы. Однако можно создать устройство, сколь угодно близкое по своим свойствам к абсолютно черному телу. Такое устройство представляет собой почти замкнутую полость, снабженную малым отверстием (рис. 3.10.3). Излучение, проникшее внутрь через отверстие, прежде чем выйти обратно из отверстия, претерпевает многократные отражения. При каждом отражении часть энергии поглощается, в результате Рис.3.10.3.

чего практически все излучение любой частоты поглощается

такой полостью. Согласно закону Кирхгофа испускательная способность такого устройства очень близка к f(ω, Т), причем Т означает температуру стенок полости. Таким образом, если стенки полости поддерживать при некоторой температуре Т, то из отверстия выходит излучение, весьма близкое по спектральному составу к излучению абсолютно черного тела при той же температуре. Проводя эксперимент и разлагая это излучение в спектр с помощью дифракционной решетки можно измерить интенсивность различных участков спектра.Такой эксперимент дает можно вид функции f(ω,Т) или φ(λ, Т). Результаты таких опытов приведены на рис.3.10.4. Разные кривые относятся к различным значениям температуры Т абсолютно черного тела. Площадь, охватываемая кривой, дает энергетическую светимость абсолютно черного тела при соответствующей температуре.

Из рис.3.10.4 следует, что энергетическая светимость абсолютно черного тела сильно возрастает с температурой. Максимум испускательной способности с увеличением темпера- Рис.3.10.4.

туры сдвигается в сторону более коротких волн.

Равновесная плотность энергии излучения

Рассмотрим излучение, находящееся в равновесии с веществом. Для этого представим себе эвакуированную полость, стенки которой поддерживаются при постоянной температуре Т. В равновесном состоянии энергия излучения будет распределена в объеме полости с определенной плотностью u = u(T). Спектральное распределение этой энергии можно охарактеризовать функцией u(ω,T), определяемой условием du_ω= u(ω,T) d 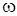, где du_ω — доля плотности энергии, приходящаяся на интервал частот dω. Полная плотность энергии u(T) связана с функцией u(ω,T) формулой (3.10.1).

Из термодинамических соображений следует, что равновесная плотность энергии излучения u(T) зависит только от температуры и не зависит от свойств стенок полости. Рассмотрим две полости, стенки которых изготовлены из разных материалов и имеют первоначально одинаковую температуру. Допустим, что равновесная плотность энергии в обеих полостях различна и, скажем, u₁(T)>u₂(T). Соединим полости с помощью небольшого отверстия (рис.3.10.5) и тем самым позволим стенкам полостей вступить в теплообмен через излучение. Так как по предположению u₁>u₂, поток энергии из первой полости во вторую должен быть больше, чем поток, текущий во встречном Рис.3.10.5

направлении. В результате стенки второй полости станут

поглощать больше энергии, чем излучать, и температура их начнет повышаться. Стенки же первой полости станут поглощать меньше энергии, чем излучать, так что они будут охлаждаться. Однако два тела с первоначально одинаковой температурой не могут вследствие теплообмена друг с другом приобрести различные температуры — это запрещено вторым началом термодинамики. Поэтому наше допущение о неодинаковости u₁ и u₂ должно быть признано неправомерным. Вывод о равенстве u₁(T) и u₂(T) распространяется на каждую спектральную составляющую u(ω, T).

Независимость равновесного излучения от природы стенок полости можно пояснить следующими соображениями. Абсолютно черные стенки поглощали бы всю упавшую на них энергию Ф_э и испускали бы такой же поток энергии Ф_э. Стенки с поглощательной способностью а поглотят долю aФ_э упавшего на них потока Ф_э и отразят поток, равный (1-a)Ф_э. Кроме того, они излучат поток aФ_э (равный поглощенному потоку). В итоге стенки полости вернут излучению такой же поток энергии Ф_э = (1-a)Ф_э + aФ_э, какой возвращали бы излучению абсолютно черные стенки.

Равновесная плотность энергии излучения u связана с энергетической светимостью абсолютно черного тела R* простым соотношением, которое мы сейчас выведем.

Рассмотрим эвакуированную полость с абсолютно черными стенками. В случае равновесия через каждую точку внутри полости будет проходить в любом направлении поток излучения одинаковой плотности. Если бы излучение распространялось Рис.3.10.6.

в одном заданном направлении (т. е. через данную точку проходил только один луч), плотность потока энергии в рассматриваемой точке была бы равна произведению плотности энергии u на скорость электромагнитной волны c. Однако через каждую точку проходит множество лучей, направления которых равномерно распределены в пределах телесного угла 4π. Поток энергии равномерно распределен в пределах этого телесного угла. Следовательно, в каждой точке в пределах телесного угла 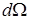будет течь поток энергии, плотность которого равна

Возьмем на поверхности полости элементарную площадку ΔS (рис.3.10.6). Эта площадка посылает в пределах телесного угла dΩ=sinυdυdφ в направлении, образующем с нормалью угол υ, поток энергии

По всем направлениям, заключенным в пределах телесного угла 2π, площадка ΔS посылает поток энергии

(3.10.13)

Вместе с тем поток энергии, испускаемый площадкой, можно найти, умножив энергетическую светимость R* на ΔS: ΔФ_э=R*ΔS. Сравнение с (3.10.13) дает, что

(3.10.14)

Равенство (3.10.14) должно выполняться для каждой спектральной составляющей излучения. Отсюда вытекает, что

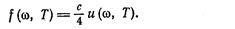(3.10.15)

Эта формула связывает испускательную способность абсолютно черного тела с равновесной плотностью энергии теплового излучения.

Закон Стефана — Больцмана и закон Вина.

Теоретическое объяснение законов излучения абсолютно черного тела имело огромное значение в истории физики – оно привело к понятию квантов энергии.

Долгое время попытки получить теоретически вид функции f(ω, Т) не давали общего решения задачи. Стефан (1879), анализируя экспериментальные данные, пришел к выводу, что энергетическая светимость R любого тела пропорциональна четвертой степени абсолютной температуры. Однако последующие более точные измерения показали ошибочность его выводов. Больцман (1884), исходя из термодинамических соображений, получил теоретически для энергетической светимости абсолютно черного тела следующее значение:

(3.10.16)

где σ – постоянная величина, Т – абсолютная температура. Таким образом, заключение, к которому Стефан пришел для нечерных тел (с абсолютно черными телами он не экспериментировал), оказалось справедливым лишь для абсолютно черных тел.

Соотношение (3.10.16) между энергетической светимостью абсолютно черного тела и его абсолютной температурой получило название закона Стефана – Больцмана. Константу σ называют постоянной Стефана – Больцмана. Ее экспериментальное значение равно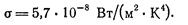

Вин (1893), воспользовавшись, кроме термодинамики, электромагнитной теорией, показал, что функция спектрального распределения должна иметь вид

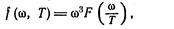(3.10.17)

где F — некоторая функция отношения частоты к температуре.

Согласно формуле (3.10.11) для функции φ(λ, Т) получается выражение

(3.10.17)

где ψ(λ, Т) некоторая функция произведения λТ.

Соотношение (3.10.17) позволяет установить зависимость между длиной волны λ_m, на которую приходится максимум функции φ(λ, Т) и температурой. Продифференцируем это соотношение по λ:

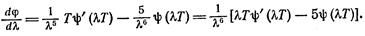(3.10.18)

Выражение в квадратных скобках представляет собой некоторую функцию Ψ(λ, Т). При длине волны λ_m, соответствующей максимуму функции φ(λ, Т), выражение (3.10.18) должно обращаться в нуль:

Из опыта известно, что λ_m конечно (λ_m ≠ ∞). Поэтому должно выполняться условие: Ψ(λ_mТ) = 0. Решение последнего уравнения относительно неизвестного λ_mТ дает для этого неизвестного некоторое число, которое мы обозначим буквой b. Таким образом, получается соотношение

которое носит название закона смещения Вина: длина волны, на которую приходится максимум излучательной способности абсолютно черного тела, обратно пропорциональна его абсолютной температуре

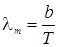. (3.10.19)

Экспериментальное значение константы b равно

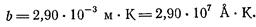
Формула Рэлея — Джинса.

Рэлей и Джинс сделали попытку определить равновесную плотность излучения u(ω, Т), исходя из теоремы классической статистики о равнораспределении энергии по степеням свободы. Они предположили, что на каждое электромагнитное колебание приходится в среднем энергия, равная двум половинкам kT – одна половинка на электрическую, вторая — на магнитную энергию волны (напомним, что по классическим представлениям на каждую колебательную степень свободы приходится в среднем энергия, равная двум половинкам kТ).

Равновесное излучение в полости представляет собой систему стоячих волн. С учетом возможных видов поляризации количество стоячих волн, отнесенное к единице объема полости, определяется формулой

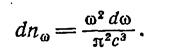(3.10.20)

Как мы уже отмечали, Рэлей и Джинс, исходя из закона равнораспределения энергии по степеням свободы, приписали каждому колебанию энергию ‹ε›, равную kT. Умножив (3.10.20) на ‹ε›, получим плотность энергии, приходящуюся на интервал частот dω:

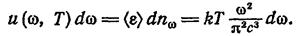
Отсюда

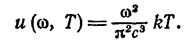(3.10.21)

Перейдя от u(ω, Т) к f(ω, Т), получим выражение для испускательной способности абсолютно черного тела:

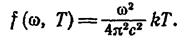(3.10.22)

Выражения (3.10.21) и (3.10.22) называются формулой Рэлея — Джинса. Эта формула удовлетворительно согласуется с экспериментальными данными лишь при больших длинах волн и резко расходится с опытом для малых длин волн (см. рис.3.10.7, на котором сплошной линией изображена экспериментальная кривая, пунктиром кривая, построенная по формуле Рэлея — Джинса).

Интегрирование выражения (3.10.22) по ω в пределах от 0 до ∞ дает для равновесной плотности энергии u(Т) бесконечно большое значение. Этот результат, получивший название ультрафиолетовой катастрофы, также находится в противоречии с опытом. Равновесие между излучением и излучающим Рис.3.10.7.

телом устанавливается при конечных значениях u(Т).

Формула Планка.

С классической точки зрения вывод формулы Рэлея—Джинса является безупречным. Поэтому расхождение этой формулы с опытом указывало на существование каких-то закономерностей, несовместимых с представлениями классической физики.

В 1900 г. Планку удалось найти вид функции u(ω, Т), в точности соответствующий опытным данным:

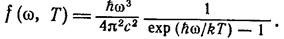(3.10.23)

Для этого ему пришлось сделать предположение совершенно чуждое классическим представлениям, а именно допустить, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых пропорциональна частоте излучения:

(3.10.24)

Коэффициент пропорциональности получил впоследствии название постоянная Планка.

Исходя из выдвинутого предположения, Планк получил значение средней энергии излучения частоты :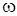

, (3.10.25)

откуда с учетом (3.10.20) и следует формула Планка.

Заметим в конце, что для малых частот, когда 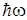« kT , выражение (3.10.25) дает классическое .

Лекция 3.11.