Явление дифракции. Зоны дифракции. Дифракция Френеля.

Под дифракцией понимают явления, наблюдаемые при распространении волн в среде с резкими неоднородностями (края экранов, отверстия и др.), что связано с отклонениями от их прямолинейного распространения. Это приводит, в частности для световых волн, к огибанию волнами препятствий и проникновению света в область геометрической тени.

Отметим, что явление дифракции наблюдается для любых волн. Мы постоянно наблюдаем дифракцию звуковых волн, волн на поверхности воды, радиоволн. Для наблюдения же дифракции световых волн необходимы специальные условия, обусловленные малостью их длин волн l.

Наблюдение дифракции света проводят обычно по такой схеме. На пути световой волны помещают непрозрачную преграду, закрывающую часть световой волны. За преградой располагают экран, на котором при определенных условиях возникает дифракционная картина в виде той или иной системы полос и пятен — максимумов и минимумов освещенности. Исследование распределения интенсивности света на экране и будет являться основной нашей задачей.

Вообще говоря, для описания дифракционных явлений не требуется вводить никаких новых принципов. В рамках электромагнитной теории света задача сводится к нахождению решения уравнений Максвелла при определенных граничных условиях. Однако решение такой задачи представляет большие математические трудности. Поэтому в большинстве случаев, представляющих практический интерес, вполне достаточным оказывается приближенный метод решения задачи о распределении интенсивности света, основанный на принципе Гюйгенса-Френеля. Именно этот принцип и основанные на нем простые и наглядные методы расчета мы и возьмем за основу дальнейшего изложения.

Принцип Гюйгенса - Френеля.

Первое объяснение дифракции света принадлежит Френелю (1818 г.). Он показал, что количественное описание дифракционных явлений возможно на основе построения Гюйгенса, если его дополнить принципом интерференции вторичных волн.

Принцип Гюйгенса устанавливает способ построения фронта волны в момент времени 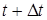по известному положению фронта в момент времени t. Согласно этому принципу каждая точка, до которой доходит волновой фронт, служит вторичным источником волн. Огибающая этих вторичных волн и дает положение волнового фронта в следующий момент времени. Френель дополнил этот принцип положением о когерентности вторичных источников. Тогда вторичные волны, придя в точку наблюдения, дадут интерференционную картину. Учет амплитуд и фаз вторичных волн позволит найти результирующую амплитуду.

Рассмотрим для примера экран Э с некоторым отверстием, через которое проходит свет от точечного монохроматического источника Р₀ (рис.3.8.1). Задача состоит в определении напряженности Е в любой точке Р за экраном.

В методе Френеля предполагается, что напряженность Е в точках отверстия такая же, как и при

отсутствии экрана, и что в точках непосредственно Рис.3.8.1.

за экраном Е = 0. Т. е. считается, что существенна

только форма отверстия экрана, но не сам экран.

Это предположение, как показал опыт, справедливо, когда размеры отверстия и его расстояния до источника и точки наблюдения Р значительно больше длины волны l, т. е. когда отклонения от геометрической оптики довольно малы. Оно нарушается для отверстия, например, щели, ширина которой значительно меньше l.

Закроем мысленно отверстие в экране произвольной поверхностью S. Разобьем эту поверхность на элементарные участки dS. По предположению Френеля каждый из этих участков становится источником вторичной сферической волны. Амплитуда вторичной световой волны, достигающей точки наблюдения Р, должна быть пропорциональна амплитуде Е первичной волны, приходящей к элементу dS, а также площади самого элемента dS, и обратно пропорциональна расстоянию r от элемента dS до точки Р.

Для определения результирующей амплитуды колебаний в точке Р, т. е. суммы элементарных амплитуд, необходимо еще учесть, что колебания от разных элементов dS достигают точки Р с разными фазами. Это приводит к появлению в выражении для результирующей амплитуды множителя cos(kr + a), где k = 2π/l, а a — дополнительная фаза, равная фазе первичной волны в элементе dS (для разных элементов она в общем случае не одинакова).

Таким образом, результирующая амплитуда напряженности Е в точке Р может быть представлена как суперпозиция элементарных амплитуд с учетом их взаимных фазовых соотношений:

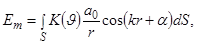(3.8.1)

где интегрирование проводится по выбранной нами поверхности S.

В интеграле (3.8.1) a₀ величина, определяемая амплитудой световой волны в месте нахождения элемента dS; К( 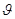) — некоторый коэффициент, зависящий от угла между первоначальным направлением световой волны в данной точке (волновым вектором 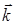) и направлением на точку Р. Естественно предположить, что коэффициент К монотонно убывает с ростом угла. Многие практически важные дифракционные задачи можно, как мы увидим далее, решить при весьма общих предположениях относительно К( 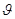), не уточняя конкретного вида зависимости его от угла .

В дальнейшем мы будем рассматривать ситуации, позволяющие в качестве поверхности S брать волновую поверхность падающей волны, что значительно упрощает расчеты. В этом случае угол в коэффициенте К( 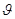) представляет собой угол между нормалью 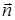к элементу поверхности dS и направлением от dS к точке Р, а дополнительную фазу a в (3.8.1) можно считать равной нулю (a = 0).

Расчет, базирующийся на принципе Гюйгенса—Френеля можно представить в простой и наглядной форме с помощью векторной (фазовой) диаграммы (рис.3.8.2)Использование подобных диаграмм в дальнейшем позволит значительно упростить многие рассуждения Рис.3.8.2.

и расчеты. На этой диаграмме результирующая амплитуда

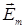представлена как векторная сумма амплитуд d 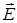колебаний в точке Р от различных элементов dS поверхности S с учетом их фаз. Разность фаз между различными векторами 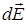на диаграмме определяет угол между этими векторами.

Полуволновые зоны. Зоны Френеля.

Суммирование (интегрирование) амплитуд элементарных колебаний, приходящих в точку Р, вообще говоря, весьма сложно. Но в простейших случаях, обладающих определенной симметрией, интегрирование может быть заменено простым алгебраическим или графическим сложением (последнее особенно наглядно).

Суммирование амплитуд колебаний, приходящих от различных элементов волновой поверхности S, Френель предложил делать с помощью разбиения поверхности S на зоны, конфигурация которых зависит от симметрии рассматриваемой задачи.

Суть метода состоит в том, чтобы разбить волновую поверхность на участки (зоны), так чтобы расстояния до точки наблюдения от краев каждой зоны отличались на половину длины волны - 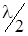. Конфигурация самих зон зависит от симметрии задачи. Эти зоны называются полуволновыми зонами. Смысл такого разбиения в том, что в этом случае волны Рис.3.8.3.

от вторичных источников приходят в точку наблюдения

со сдвигом по фазе на 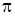и при интерференции гасят друг друга. Это, как мы убедимся в дальнейшем, существенно упрощает расчет.

Частным случаем полуволновых зон являются зоны Френеля. В этом случае зоны представляют собой кольца, которые симметричны относительно линии 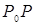, где 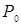- источник, а Р – точка наблюдения (рис.3.8.3). Эти зоны выбираем так, чтобы расстояния от краев каждой зоны до точки Р отличались друг от друга на половину длины волны. Рис.3.8.4.

Найдем внешний радиус m-й зоны Френеля, r_m.

С этой целью воспользуемся рисунком 3.8.4. Из него видно, что

,

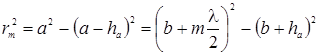где а – радиус волновой поверхности, отрезок ВО равен 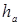. Раскрыв это выражение и учитывая, что при на очень больших т членами, которые входит 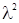можно пренебречь, получим

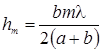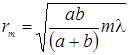; . (3.8.2)

Заметим, что если падающая нормально на данное отверстие волна плоская (а®µ), то

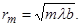(3.8.4)

Используя формулу площади сферическогосегмента, получим площадь т-ой зоны 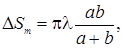(3.8.5)

т. е. практически одинаковы для всех зон. Однако, амплитуды колебаний, приходящих в точку Р от вторичных источников этих зон, монотонно и слабо убывают из-за увеличения расстояния r до точки Р от каждой следующей зоны и роста угла между нормалью к элементам зоны и направлением на точку Р.

Спираль Френеля.

Рассмотрим графический метод сложения амплитуд. В этом простом и наглядном методе каждую полуволновую зону Френеля дополнительно мысленно разбивают на весьма узкие кольцевые зоны. Амплитуду колебаний, создаваемых вторичными источниками каждой из таких зон, изобразим вектором d 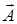. Вследствие увеличения расстояния r и уменьшения коэффициента К амплитуда колебаний, создаваемых каждой следующей узкой кольцевой зоной, будет убывать по модулю и отставать по фазе от колебаний, создаваемых предыдущей зоной. Изобразив отставание по фазе поворотом каждого вектора d 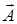против часовой стрелки на соответствующий угол, получим цепочку векторов, векторная сумма которых и есть результирующая амплитуда колебаний в точке Р.

На рис.3.8.5a показан результат действия 1-й зоны Френеля. Здесь амплитуда колебаний dA_N от узкого кольца, прилегающего к границе 1-й зоны Френеля, отстает по фазе на π от амплитуды колебаний, приходящих в точку Р из центра 1-й зоны — от точки

Рис.3.8.5.

О - поэтому соответствующие этим амплитудам векторы взаимно противоположны по направлению.

Продолжая построение, получим векторную диаграмму для результирующей амплитуды колебаний в точке Р от действия первых двух зон Френеля (рис.3.8.5б), затем от первых трех зон Френеля (рис.3.8.5в) и т. д. Цепочка по мере увеличения числа узких кольцевых зон будет “закручиваться” в спираль, и в результате амплитуда от действия

всех зон (всей волновой поверхности) будет равна А_µ (рис.3.8.6). Эту спираль называют спиралью Френеля. Квадрат этой величины Рис.3.8.6.

характеризует интенсивность в точке Р, если волна

распространяется в отсутствие всяких преград (полностью открытый волновой фронт).

При построении векторной диаграммы мы получаем спираль (а не окружность), так как амплитуды, создаваемые отдельными зонами, как уже говорилось, монотонно слабо убывают.

Дифракция Френеля от круглого отверстия и круглого диска.

Используя разобранный метод, можно достаточно легко решить задачу о дифракции от простейших преград.

1.Дифракция от круглого отверстия.

Пусть на пути сферической волны расположен непрозрачный экран с круглым отверстием радиуса r, расположенный так, чтобы перпендикуляр, опущенный из источника, попал в центр отверстия (рис.3.8.3). На продолжении этого перпендикуляра расположена точка наблюдения Р. Число зон m в отверстии мы можем изменять. Например, для увеличения числа зон надо или расширить отверстие, или приблизить экран к нему, или то и другое вместе. Как видно из рис.3.8.5, результирующая амплитуда, а значит и интенсивность, зависит от того, четное или нечетное число m зон Френеля умещается в отверстии — для точки наблюдения Р. Если число зон нечетное, в точке Р наблюдается максимум, если же число зон четное, то — минимум.

Таким образом, амплитуда колебаний и интенсивность света в точке Р по мере увеличения радиуса отверстия в экране изменяется не монотонно. Пока открывается первая зона Френеля, амплитуда в точке Р увеличивается и достигает максимума при полностью открытой зоне. Но по мере открывания второй зоны Френеля амплитуда колебаний в точке Р убывает, и при полностью открытых двух первых зонах уменьшается почти до нуля. Затем амплитуда увеличивается снова и т. д.

То же самое будет наблюдаться, если вместо увеличения отверстия приближать к нему точку наблюдения Р вдоль прямой Р₀Р. Это легко понять из рисунка: при этом число открываемых зон Френеля в отверстии экрана Э будет увеличиваться.

На первый взгляд эти результаты, предсказанные на основе принципа Гюйгенса-Френеля, выглядят парадоксальными. Однако они хорошо подтверждаются опытом. В то же время согласно геометрической оптике интенсивность света в точке Р не должна зависеть от радиуса отверстия.

Итак, амплитуда колебаний в точке Р от полностью открытой волновой поверхности, согласно представлениям Френеля, равна А_µ = А₁/2, т. е. интенсивность (I ~ А²) в четыре раза меньше, чем при наличии экрана с круглым отверстием, открывающем только 1-ю зону Френеля.

Особенно неожиданным в методе Френеля представляется тот удивительный вывод, что при отверстии в экране, открывающем для точки Р две зоны Френеля, интенсивность в этой точке падает практически до нуля, хотя световой поток через отверстие оказывается вдвое больше.

Нужно однако заметить, что такое чередование ярких максимумов и почти нулевых минимумов будет наблюдаться лишь в случае, когда отверстие оставляет открытым лишь небольшое число зон Френеля. Если же число открытых зон очень велико, то, как видно из рис.3.8.6, разница в интенсивности при четном и нечетном числе зон становится очень маленькой. Практически в этом случае в точке Р всегда наблюдается максимум и интенсивность такова, как будто никакой преграды нет. Такая ситуация называется геометрической оптикой.

Метод зон Френеля позволяет сравнительно просто найти интенсивность света только в точке Р, лежащей на оси круглого отверстия в экране. Расчет же распределения интенсивности для всей дифракционной картины значительно сложнее. Вся картина обладает круговой симметрией и представляет собой чередующиеся светлые и темные кольца, плавно переходящие друг в друга.

Если в отверстии экрана укладывается 1-я зона Френеля или ее часть, то интенсивность максимальна в центре картины (т. е. в точке Р) и монотонно убывает при удалении от точки Р. Если отверстие в экране открывает две первые зоны Френеля, то в окрестности Рис.3.8.7.

точки Р возникает темное круглое пятно, а вокруг него – светлое кольцо. С увеличением числа m открытых зон в отверстии экрана увеличивается и число светлых и темных колец. На рис.3.8.7 показано распределение интенсивности I от расстояния r до центра дифракционной картины при различном числе m открытых зон Френеля. Когда же в отверстии укладывается большое число зон Френеля, интенсивность вблизи точки Р оказывается почти равномерной и лишь у краев геометрической тени отверстия наблюдается чередование весьма узких светлых и темных кольцевых полос.

2.Дифракция от круглого экрана (преграды). Пусть теперь на пути волны расположен непрозрачный круглый диск. В центре его геометрической тени интенсивность не равна нулю. Если диск перекрывает лишь несколько зон Френеля, то интенсивность в центре геометрической тени почти такая же, как при отсутствии диска. Это непосредственно следует из спирали Френеля (рис.3.8.8), поскольку если диск закрывает, скажем, 1,5 зоны Френеля, то результирующий вектор 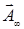при полностью открытой волновой поверхности можно представить как сумму Рис.3.8.8.

двух векторов: 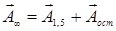Так как первые полторы зоны

закрыты, то остается только вектор 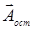‑ от всех остальных зон. Этот вектор по модулю лишь немного меньше вектора .

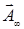Это светлое пятно в центре геометрической тени называют пятном Пуассона. Рассматривая в свое время метод Френеля, Пуассон пришел к выводу, что в центре тени от диска должно быть светлое пятно, но счел этот вывод столь абсурдным, что выдвинул его как убедительное возражение против волновой теории, развиваемой Френелем. Однако это “абсурдное” предсказание было экспериментально подтверждено Арагоном. Волновая теория Френеля восторжествовала.

Приведенный вывод также справедлив при небольшом числе закрытых зон Френеля. Если число закрытых зон очень велико, в центре картины будет наблюдаться минимум близкий к нулю (геометрическая оптика).

Зонная пластинка.

Если в экране открыть только нечетные зоны Френеля (1-ю, 3-ю,...), то векторы-амплитуды от этих зон будут сонаправлены и в сумме дадут в центре картины вектор, во много раз превосходящий по модулю векторы А_µ и А₁. Такой экран называют амплитудной зонной пластинкой. Аналогично можно изготовить зонную пластинку, где открыты только четные зоны Френеля.

Зонная пластинка, содержащая n открытых зон, создает в точке Р интенсивность приблизительно в n² раз большую, чем отверстие в первую зону Френеля.

Еще большего эффекта можно достичь, не закрывая четные (или нечетные) зоны, а изменяя фазу колебаний волн, пришедших от этих зон, на 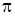. Это можно осуществить с помощью прозрачной пластинки, толщина которой в местах, соответствующих четным (или нечетным) зонам отличается на должным образом подобранную величину, так чтобы ход волны в местах соответствующих четным и нечетным зонам отличался на 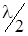. Такая пластинка называется фазовой зонной пластинкой. Такая пластинка дает увеличение амплитуды еще в два раза, а интенсивности в четыре. Примером такой пластинки является собирающая линза. Усиление интенсивности света фазовой зонной пластинкой эквивалентно фокусирующему действию линзы.

Дополнительные замечания.

Вычисления, выполненные на основе принципа Гюйгенса‑Френеля, дают, как показывает опыт, правильное распределение интенсивности при дифракции, т.е. позволяют найти правильное значение амплитуды результирующей волны в любой точке экрана, если размеры отверстий или препятствий соизмеримы с длиной волны l, другими словами, при не очень больших углах дифракции.

При этом, однако, в методе расчета Френеля есть принципиальные неясности. Главные из них заключаются в следующем.

1.При вычислении результатов интерференции элементарных волн приходится считать, что амплитуда колебаний от элементов dS волновой поверхности зависит от угла 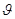между нормалью к элементу dS и направлением на точку Р, для которой ведется расчет. Амплитуда максимальна при 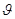= 0 и монотонно убывает до нуля при стремлении 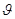к π/2, т. е. нет обратной волны. Это обстоятельство остается не обоснованным в теории Френеля.

2. Расчет по методу Френеля дает неправильное значение фазы результирующего колебания. Для полностью открытой волновой поверхности она отличается на π/2 от действительной. Это видно из рисунка спирали Френеля. Направление спирали Френеля в ее начале дает в точке наблюдения фазу колебаний от центрального элемента первой зоны. Это и есть то значение фазы, которое соответствует действительности. Результирующий же вектор от полностью открытой волновой поверхности повернут на π/2 против часовой стрелки, т. е. отстает по фазе на π/2. Таким образом, постулат Френеля, правильно задавая амплитуды вспомогательных источников, неудачно определяет их фазы.

Однако, для большинства задач вопрос о фазе не имеет значения, ибо нас интересует интенсивность результирующей волны, которая пропорциональна квадрату амплитуды. Значение же интенсивности метод Френеля дает правильное.

Итак, несмотря на некоторые недостатки, метод Френеля в вопросах расчета интенсивности волн для многих случаев является весьма плодотворным.

Зоны дифракции.

Как уже указывалось, характер дифракционной картины зависит от размеров препятствия. Рассмотренная нами ранее картина, которая носит название дифракции Френеля, наблюдается, когда отверстие оставляет открытыми лишь несколько зон Френеля. Напомним, что тогда в центре картины наблюдается чередование максимумов и минимумов в зависимости от числа открытых зон.

Также ранее отмечалось, что если число открытых зон очень велико, то разница в интенсивности при четном или нечетном числе открытых зон мала и лишь у краев геометрической тени отверстия наблюдается чередование весьма узких светлых и темных полос. В этом случае оказывается применимым приближение геометрической оптики.

И, наконец, если отверстие оставляет открытой лишь малую часть первой зоны Френеля, то лучи от вторичных источников идут в точку наблюдения практически параллельно и в центре картины никогда не будет минимума. Такой случай носит название дифракции Фраунгофера.

Количество «работающих» зон Френеля можно оценить из формулы (3.8.4). Тогда мы получаем параметр, по значению которого можно определить к какой зоне дифракции относится рассматриваемая в данной задаче ситуация. Тогда можно записать:

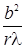« 1 - дифракция Фраунгофера,

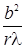~ 1 - дифракция Френеля, (3.8.6)

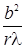» 1 - геометрическая оптика,

где b - расстояние от преграды до точки наблюдения картины, r - размер преграды (неоднородности), 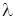- длина волны.

Лекция 3.9