Интерференция. Условия максимума и минимума интерференции.
Интерференция - это явление наложения двух или нескольких волн, при котором результирующая интенсивность не равна сумме интенсивностей складываемых волн. Интерферировать могут волны любой физической природы. Мы рассмотрим это явление на примере электромагнитных волн.
Пусть в некоторую точку пространства приходят две плоские электромагнитные волны
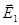 =
= 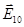 cos(
cos( 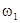 t─
t─ 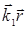 +
+ 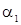 ),
),
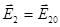 cos (
cos ( 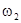 t─
t─ 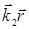 +
+ 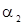 ). (3.6.1) Они возбуждают в этой точке колебания напряженности электрического поля
). (3.6.1) Они возбуждают в этой точке колебания напряженности электрического поля
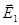 =
= 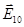 cos(
cos( 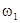 t +
t + 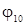 ),
),
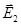 =
= 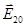 cos(
cos( 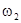 t +
t + 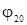 ), (3.6.2) где
), (3.6.2) где 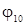 и
и 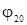 - соответствующие начальные фазы. Результирующая напряженность, в соответствии с принципом суперпозиции,
- соответствующие начальные фазы. Результирующая напряженность, в соответствии с принципом суперпозиции,
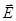 =
= 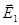 +
+ 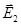 .
.
Интенсивность волны пропорциональна среднему по времени квадрату напряженности электрического поля:
I ~ < 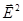 > = < (
> = < ( 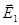 +
+ 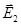 )
) 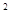 > = <
> = < 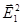 > + <
> + < 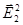 > + 2 < (
> + 2 < ( 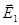 ·
· 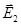 )> (3.6.3)
)> (3.6.3)
Здесь усреднение проводится за время наблюдения. Фактически всякий прибор, с помощью которого наблюдают интерференционную картину, обладает некоторой инерционностью, т.е. регистрирует не мгновенную картину, а усредненную за промежуток времени 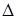 t, необходимый для «срабатывания» прибора. Это и есть время усреднения в (3.6.3).
t, необходимый для «срабатывания» прибора. Это и есть время усреднения в (3.6.3).
Первые два слагаемых в правой части (3.6.3) определяют (с учетом коэффициента пропорциональности) интенсивности волн I 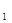 и I
и I 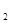 . Интерференция будет наблюдаться, если третье слагаемое будет отличаться от нуля. Для этого вектора
. Интерференция будет наблюдаться, если третье слагаемое будет отличаться от нуля. Для этого вектора 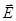
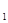 и
и 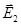 не должны быть взаимно перпендикулярны. В дальнейшем будем полагать, что
не должны быть взаимно перпендикулярны. В дальнейшем будем полагать, что 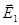 и
и 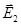 параллельны. Рассмотрим идеализированный случай монохроматических плоских волн, т.е. амплитуды, частоты и волновые векторы (
параллельны. Рассмотрим идеализированный случай монохроматических плоских волн, т.е. амплитуды, частоты и волновые векторы ( 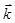 ) будем полагать константами, причем
) будем полагать константами, причем
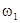 =
= 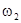 =
= 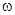 , |
, | 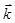
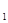 | = |
| = | 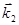 | = k.
| = k.
Однако параллельность векторов 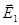 и
и 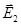 еще не гарантирует отличие от нуля последнего слагаемого в (3.6.3). Для выполнения этого условия необходимо, чтобы модуль амплитуды результирующего колебания в данной точке не ме
еще не гарантирует отличие от нуля последнего слагаемого в (3.6.3). Для выполнения этого условия необходимо, чтобы модуль амплитуды результирующего колебания в данной точке не ме 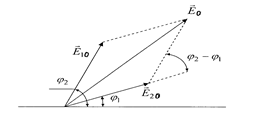 нялся за время наблюдения. Это возможно лишь в случае, если разность фаз складываемых в этой точке колебаний
нялся за время наблюдения. Это возможно лишь в случае, если разность фаз складываемых в этой точке колебаний  (
( 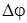 =
= 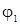 —
— 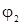 ) не зависит от времени. Рис.3.6.1.
) не зависит от времени. Рис.3.6.1.
Условия максимума и минимума интерференции.
Модуль амплитуды результирующего колебания Е 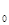 в случае параллельности складываемых колебаний можно определить с помощью векторной диаграммы (рис. 3.6.1)
в случае параллельности складываемых колебаний можно определить с помощью векторной диаграммы (рис. 3.6.1)
Е 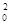 = Е
= Е 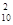 + Е
+ Е 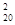 + 2 Е
+ 2 Е 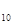 Е
Е 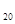 cos (
cos ( 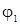 —
— 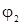 ) . (3.6.4)
) . (3.6.4)
Тогда результирующая интенсивность
I = I 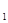 + I
+ I 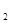 + 2
+ 2 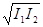 <cos (
<cos ( 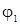 —
— 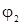 ) >. (3.6.5)
) >. (3.6.5)
В реальных источниках излучателями являются отдельные атомы, не связанные друг с другом ( 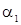 и
и 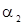 меняются независимо). Поэтому разность фаз (
меняются независимо). Поэтому разность фаз ( 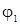 —
— 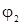 ) непрерывно изменяется, принимая с равной вероятностью любые значения, так что среднее по времени значение <cos(
) непрерывно изменяется, принимая с равной вероятностью любые значения, так что среднее по времени значение <cos( 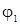 ─
─ 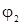 )> равно нулю.
)> равно нулю.
Тогда суммарная интенсивность равна сумме интенсивностей складываемых волн – интерференция отсутствует.
Если же добиться, чтобы разность фаз в каждой точке пространства оставалась неизменной с течением времени, то значение интенсивности в разных точках пространства будет отличным от суммы интенсивностей складываемых волн и различным в разных точках в зависимости от величины cos ( 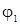 —
— 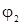 ). В частности, при cos (
). В частности, при cos ( 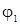 —
— 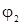 ) = 1 интенсивность будет принимать максимальное значение:
) = 1 интенсивность будет принимать максимальное значение:
I 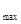 =I
=I 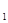 +I
+I 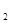 +2
+2 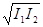 =
= 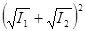 . (3.6.6) Как нетрудно видеть, такая интенсивность будет осуществляться при
. (3.6.6) Как нетрудно видеть, такая интенсивность будет осуществляться при 
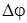 =
= 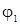 —
— 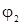 =2m
=2m 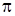 , (3.6.7) где целое число m = 0, 1, 2, …называется порядком максимума интерференции. Если cos (
, (3.6.7) где целое число m = 0, 1, 2, …называется порядком максимума интерференции. Если cos ( 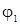 —
— 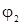 ) = —1, интенсивность будет минимальна:
) = —1, интенсивность будет минимальна:
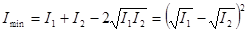 . (3.6.8) Такая интенсивность наблюдается в точках, где
. (3.6.8) Такая интенсивность наблюдается в точках, где
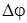 =
= 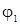 ─
─ 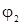 = ( 2m + 1)
= ( 2m + 1) 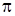 . (3.6.9) Условия (3.6.7) и (3.6.9) называют условиями соответственно максимума и минимума интерференции.
. (3.6.9) Условия (3.6.7) и (3.6.9) называют условиями соответственно максимума и минимума интерференции.
Волны, в которых вектора 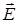 образуют угол не равный
образуют угол не равный 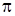 /2 и разность фаз колебаний в каждой точке не меняется с течением времени, называются когерентными. Интерференционную картину могут дать только такие волны.
/2 и разность фаз колебаний в каждой точке не меняется с течением времени, называются когерентными. Интерференционную картину могут дать только такие волны.
Фаза колебаний, возбуждаемых волной в некоторой точке пространства, зависит от расстояния, пройденного волной (x) и показателя преломления среды, в которой она распространяется (n).Фаза волны (для плоской волны)
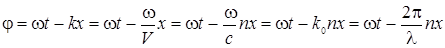 .
.
Величина s = nx называется оптическим ходом волны, а 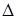 =(s
=(s 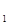 –s
–s 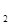 )─ оптической разностью хода волн. Разность фаз колебаний в данной точке, которую будем в дальнейшем обозначать
)─ оптической разностью хода волн. Разность фаз колебаний в данной точке, которую будем в дальнейшем обозначать 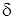 и оптическая разность хода волн связаны соотношением
и оптическая разность хода волн связаны соотношением
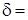
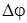 =
= 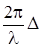 , (3.6.10)
, (3.6.10)
где 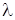 – длина волны в вакууме,
– длина волны в вакууме, 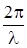 = k
= k 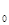 – волновое число в вакууме. Тогда условия возникновения максимумов и минимумов интенсивности можно записать:
– волновое число в вакууме. Тогда условия возникновения максимумов и минимумов интенсивности можно записать:
I = I 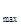 , если
, если 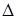 = m
= m 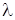 ; (3.6.11)
; (3.6.11)
I = I 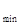 , если
, если 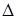 = (2т+1)
= (2т+1) 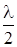 . (3.6.12)
. (3.6.12)
Однако все вышеизложенное справедливо лишь для монохроматических волн. При наложении волн от двух реальных источников или даже от разных участков одного и того же протяженного источника интерференция не наблюдается. Следовательно, независимые источники некогерентны. Причиной этого является сам механизм излучения света атомами источника. Атом, получивший избыточную энергию (перешедший в возбужденное состояние), затем в течение очень короткого промежутка времени ( ≈10 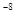 с) излучает электромагнитную волну (цуг) и возвращается в нормальное (невозбужденное) состояние. Спустя некоторое время атом может вновь возбудиться и вновь излучить короткий импульс (цуг волны), причем заметим, что атомы излучают независимо друг от друга со случайными начальными фазами, беспорядочно изменяющимися от одного акта излучения к другому. Поэтому спонтанно излучающие атомы представляют собой некогерентные источники.
с) излучает электромагнитную волну (цуг) и возвращается в нормальное (невозбужденное) состояние. Спустя некоторое время атом может вновь возбудиться и вновь излучить короткий импульс (цуг волны), причем заметим, что атомы излучают независимо друг от друга со случайными начальными фазами, беспорядочно изменяющимися от одного акта излучения к другому. Поэтому спонтанно излучающие атомы представляют собой некогерентные источники.
Для получения когерентных волн применяют метод разделения волны от одного источника на две или несколько систем волн, так чтобы в каждой из них было представлено излучение одних и тех же атомов источника. Такие волны в силу общности происхождения когерентны и могут создать интерференционную картину. Принципиально возможны два метода получения таких систем: метод деления волнового фронта (опыт Юнга, бипризма Френеля и т.д. ) и метод деления амплитуды или деление по ходу волны ( интерференция в тонких пленках). При этом чтобы новые волны были когерентны при делении волнового фронта, необходимо соблюдение некоторых условий, о которых речь пойдет далее.
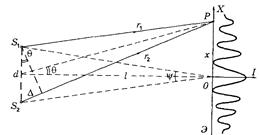 Образовавшиеся после разделения вóлны во всех интерференционных схемах можно представить как бы исходящими из двух точечных источников S1 и S2 (действительных Рис.3.6.2.
Образовавшиеся после разделения вóлны во всех интерференционных схемах можно представить как бы исходящими из двух точечных источников S1 и S2 (действительных Рис.3.6.2.
или мнимых — это не существенно). Поэтому общий подход к интерпретации получаемых результатов будет единым, с него мы и начнем.
Рассмотрим две волны, исходящие из когерентных источников S1 и S2 (рис.3.6.2). Пусть волны распространяются в вакууме. В области, где эти волны перекрываются — ее называют зоной интерференции — должна возникать система чередующихся максимумов и минимумов освещенности, которую можно наблюдать на экране Э.
Разность расстояний r2 и r1 от источников до интересующей нас точки P D = r2 ‑ r1 представляет собой разность хода волн. В точках на экране, где выполняется условие (3.6.11), наблюдается максимум интенсивности, а в точках, где выполняется (3.6.12) – минимум.
В случае, когда волны от источников распространяются не в вакууме, а в среде с показателем преломления n под D следует понимать не геометрическую, а оптическую разность хода интерферирующих волн: D = n(r2 ‑ r1). При этом l — это по-прежнему длина волны в вакууме.
Найдем координаты точек на экране, где наблюдаются интерференционные максимумы и минимумы. В практически важных случаях расстояние от источников до экрана l много больше расстояния между ними d (угол θ мал) (см. рис.3.6.2)) и разность хода D можно записать как D =d∙sin 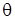 =d·θ. А так как θ » x/l, то для максимумов, согласно (3.6.11), получим d·x
=d·θ. А так как θ » x/l, то для максимумов, согласно (3.6.11), получим d·x 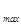 /l = ml, откуда координата максимума
/l = ml, откуда координата максимума 
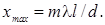 (3.6.13)
(3.6.13)
В точке x = 0 расположен максимум, соответствующий нулевой разности хода. Для него порядок интерференции m = 0. Это центр интерференционной картины. При переходе к соседнему максимуму m меняется на единицу и x — на величину Dx, которую называют шириной интерференционной полосы. Таким образом,
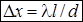 или
или 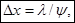 (3.6.14)
(3.6.14)
где y угол, под которым видны оба источника из центра экрана, y = d/l (см. рис.3.6.2).
Проведя аналогичные выкладки, найдем координату минимума
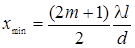 . (3.6.15)
. (3.6.15)
Ширину интерференционной полосы можно найти и как расстояние между соседними минимумами. Соответствующий расчет даст также соотношение (3.6.14)
Из этих формул видно, что для увеличения ширины полосы следует увеличивать l, или уменьшать d, или то и другое, т. е. в конечном счете — уменьшать угловое расстояние y между источниками. Полезно иметь в виду, что размер интерференционной картины обычно не превышает 1 мм, это при расстоянии от источников до экрана порядка нескольких десятков сантиметров.
Практически для получения более яркой интерференционной картины в качестве источников S1 и S2 используют две щели (или изображения исходного источника – щели S), и интерференционная картина имеет вид чередующихся светлых и темных полос, параллельных данным щелям.
Найдем распределение интенсивности на экране. Рассмотрим идеализированный случай, когда источники S1 и S2 строго монохроматические. В интересующую нас точку экрана колебания от этих источников будут приходить практически с одинаковой амплитудой, A1 = A2 = A0. Тогда, согласно (3.6.4),
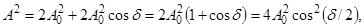 (3.6.16)
(3.6.16)
где d — разность фаз. D/l. В нашем случае d = 2π d·x/ll. Имея в виду, что интенсивность I пропорциональна квадрату амплитуды A2, получим
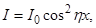 (3.6.17)
(3.6.17)
где h = πd/ll, I0 – интенсивность в максимумах (в минимумах I = 0). Полученное идеализированное распределение интенсивности I(x) несколько отличается, естественно, от реального, которому соответствует рисунок.
Способы получения интерференционной картины.
Как уже было сказано, существуют два способа разделения волны от одного источника на две части, чтобы потом они могли дать интерференционную картину. Рассмотрим примеры.
|
|
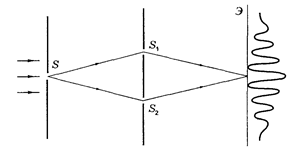 1.Разделение волны по фронту. Примером такого способа является классический опыт Юнга. Он был впервые осуществлен английским физиком Томасом Юнгом в 1807 году. В нем яркий пучок солнечного света освещал узкую щель S (рис.3.6.3). Прошедший через щель свет вследствие дифракции образует расходящуюся волну, которая падает на две узкие щели S1 и S2. Эти щели действуют как вторичные когерентные источники, и Рис.3.6.3.
1.Разделение волны по фронту. Примером такого способа является классический опыт Юнга. Он был впервые осуществлен английским физиком Томасом Юнгом в 1807 году. В нем яркий пучок солнечного света освещал узкую щель S (рис.3.6.3). Прошедший через щель свет вследствие дифракции образует расходящуюся волну, которая падает на две узкие щели S1 и S2. Эти щели действуют как вторичные когерентные источники, и Рис.3.6.3.
исходящие из них дифрагированные волны, перекрываясь, дают на экране Э систему интерференционных полос. Проведя расчет как было показано выше, можно найти координаты максимумов и минимумов на экране и ширину интерференционных полос. Однако в опыте Юнга простая картина интерференции
 осложняется еще явлениями дифракции у краев
осложняется еще явлениями дифракции у краев
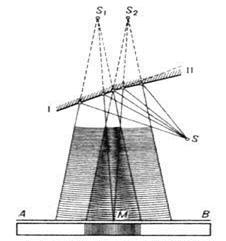
Рис 3.6.4. каждого из отверстий. Несколько позднее французский физик Френель предложил метод получения когерентных волн, при котором интерференцию можно наблюдать в более простых, физически более чистых условиях. Схема опыта приведена на рис.3.6.4. Здесь l и ll - два зеркала. Их отражающие поверхности составляют угол близкий к 180  . Перед зеркалами помещают точечный источник света S. Построив изображения точки S в зеркалах, получаем мнимые источники S
. Перед зеркалами помещают точечный источник света S. Построив изображения точки S в зеркалах, получаем мнимые источники S 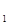 и S
и S 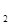 . Пучки света от этих изображений, пересекаясь под малым углом S
. Пучки света от этих изображений, пересекаясь под малым углом S 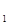 MS
MS 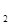 дают интерференционную картину на экране АВ. Существует и ряд других способов разделения волны по волновому фронту: бипризма Френеля, зеркало Ллойда и т.д.
дают интерференционную картину на экране АВ. Существует и ряд других способов разделения волны по волновому фронту: бипризма Френеля, зеркало Ллойда и т.д.
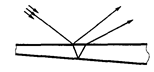
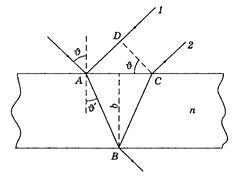 2.Разделение волны по амплитуде (по ходу волны). Примером такого способа является интерференция в тонких пленках. Пусть на прозрачную плоскопараллельную пластинку падает плоская монохроматическая световая волна, направление распространения которой показано падающим лучом на рис.3.6.5. В результате отражений от обеих поверхностей пластинки исходная волна расщепится на две, что и показано лучами 1 и 2. Амплитуды этих волн мало отличаются друг от друга — это важно для получения достаточно контрастной интерференции.
2.Разделение волны по амплитуде (по ходу волны). Примером такого способа является интерференция в тонких пленках. Пусть на прозрачную плоскопараллельную пластинку падает плоская монохроматическая световая волна, направление распространения которой показано падающим лучом на рис.3.6.5. В результате отражений от обеих поверхностей пластинки исходная волна расщепится на две, что и показано лучами 1 и 2. Амплитуды этих волн мало отличаются друг от друга — это важно для получения достаточно контрастной интерференции.
Заметим, что, кроме этих двух отраженных
волн (1 и 2), возникает еще многократное отражение. Однако их вклад практически пренебрежимо мал, и мы ограничимся только волнами, возникшими при однократном отражении.
Оптическую разность хода волн 1 и 2 Рис.3.6.5.
определим, согласно рисунку, как
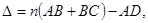 (3.6.18)
(3.6.18)
где n — показатель преломления вещества пластинки. Кроме того, видно, что AB = BC = 2b/соs 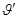 и AD = 2btg
и AD = 2btg 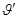 ·sin
·sin 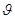 , b — толщина пластинки. В результате подстановки этих выражений в (3.6.18) получим
, b — толщина пластинки. В результате подстановки этих выражений в (3.6.18) получим
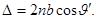 (3.6.19)
(3.6.19)
Следует также учесть, что при отражении от верхней поверхности пластинки, от среды, оптически более плотной (вокруг пластинки находится воздух, показатель преломления которого можно полагать равным единице), в соответствии с (3.3.7) происходит скачок фазы на π у отраженной волны, т. е., как говорят, “потеря” полуволны ( 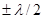 ). Учитывая еще, что по закону преломления sin
). Учитывая еще, что по закону преломления sin 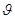 = n·sin
= n·sin 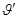 , получим
, получим
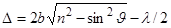 (3.6.20)
(3.6.20)
(здесь можно было написать и 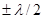 , но это не существенно).
, но это не существенно).
Если отраженные волны 1 и 2 когерентны между собой, то максимумы отражения будут наблюдаться при условии
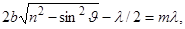 (3.6.21)
(3.6.21)
где m — целое число (порядок интерференции), а минимумы при условии
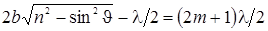 (3.6.22)
(3.6.22)
Меняя угол падения 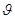 , мы будем наблюдать последовательную смену максимумов и минимумов отражения. (Заметим, что при минимуме отражения наблюдается максимум проходящего через пластинку света, и наоборот.)
, мы будем наблюдать последовательную смену максимумов и минимумов отражения. (Заметим, что при минимуме отражения наблюдается максимум проходящего через пластинку света, и наоборот.)
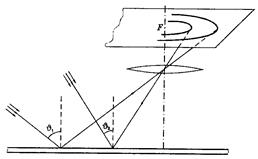 Итак, мы выяснили, что при падении плоской световой волны на плоскопараллельную тонкую пластинку интенсивность отраженного света зависит от угла падения. Изменяя этот угол, мы будем наблюдать чередование максимумов и минимумов отраженного света. Это можно использовать для получения интерференционной картины в виде привычной системы полос. Достаточно использовать в качестве падающего рассеянный монохроматический свет (он содержит волны, падающие на Рис.3.6.6.
Итак, мы выяснили, что при падении плоской световой волны на плоскопараллельную тонкую пластинку интенсивность отраженного света зависит от угла падения. Изменяя этот угол, мы будем наблюдать чередование максимумов и минимумов отраженного света. Это можно использовать для получения интерференционной картины в виде привычной системы полос. Достаточно использовать в качестве падающего рассеянный монохроматический свет (он содержит волны, падающие на Рис.3.6.6.
пластинку одновременно под разными углами),
а на пути отраженного света поставить линзу и в ее фокальной плоскости экран (рис.3.6.6).
Максимумы на экране будут располагаться в местах, соответствующих условию (3.6.21). Полоса данного порядка интерференции обусловлена светом, падающим на пластинку под одним и тем же углом 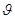 , но с разных направлений. Поэтому такие полосы называют полосами равного наклона. При расположении линзы как показано на рис.3.6.6, эти полосы имеют вид концентрических колец с центром в ее фокусе F. Порядок интерференции m растет с уменьшением угла падения
, но с разных направлений. Поэтому такие полосы называют полосами равного наклона. При расположении линзы как показано на рис.3.6.6, эти полосы имеют вид концентрических колец с центром в ее фокусе F. Порядок интерференции m растет с уменьшением угла падения  , и в центре картины он максимален.
, и в центре картины он максимален.
В белом свете интерференционные полосы окрашены, поскольку условия максимума для разных длин волн соответствуют разным углам падения света. Поэтому такое явление называют цвета тонких пластинок.
 Пусть теперь стеклянная пластинка имеет форму клина с углом раствора a << 1, и на нее падает плоская монохроматическая световая волна. Теперь отраженные от поверхностей клина световые волны будут распространяться не в одном направлении, а под некоторым углом (рис.3.6.7) Рис.3.6.7.
Пусть теперь стеклянная пластинка имеет форму клина с углом раствора a << 1, и на нее падает плоская монохроматическая световая волна. Теперь отраженные от поверхностей клина световые волны будут распространяться не в одном направлении, а под некоторым углом (рис.3.6.7) Рис.3.6.7.
Так как разность хода лучей, отразившихся от различных участков клина, неодинакова из-за различия толщины пластинки в разных местах, в области локализации интерференции появятся светлые и темные полосы, параллельные ребру клина. Каждая из таких полос возникает в результате отражений от участков клина с одинаковой толщиной, поэтому их называют полосами равной толщины.
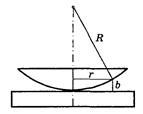 Частным случаем полс равной толщины являются кольца Ньютона. Кольца Ньютона — это кольцевые полосы равной толщины, наблюдаемые при отражении света от поверхностей зазора между стеклянной пластинкой и соприкасающейся с ней выпуклой линзой (рис.3.6.8). Волна, отраженная от верхней поверхности линзы, в силу небольшой длины когерентности обычных источников света, некогерентна с волнами, отраженными от поверхностей зазора, и участия в образовании Рис.3.6.8.
Частным случаем полс равной толщины являются кольца Ньютона. Кольца Ньютона — это кольцевые полосы равной толщины, наблюдаемые при отражении света от поверхностей зазора между стеклянной пластинкой и соприкасающейся с ней выпуклой линзой (рис.3.6.8). Волна, отраженная от верхней поверхности линзы, в силу небольшой длины когерентности обычных источников света, некогерентна с волнами, отраженными от поверхностей зазора, и участия в образовании Рис.3.6.8.
интерференционной картины не принимает. Поэтому мы ее и не будем учитывать.
При нормальном падении света кольца в отраженном свете имеют вид концентрических окружностей с центром в точке соприкосновения линзы с пластинкой. Найдем радиусы r темных колец (минимумов).
Сначала запишем условие образования темных колец. Они возникают там, где оптическая разность хода волн D, отраженных от обеих поверхностей зазора, равна нечетному числу полуволн:
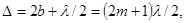
где l/2 связано с “потерей” полуволны при отражении от пластинки и m = 0, 1, 2, ... . Отсюда
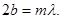 (3.6.23)
(3.6.23)
Далее, согласно теореме Пифагора r2 = R2 - (R - b)2. Учитывая, что b << R, получим 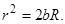 (3.6.24)
(3.6.24)
Из (3.6.23) и (3.6.24) следует, что радиус m-го темного кольца
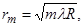 m=0, 1, 2 … (3.6.25)
m=0, 1, 2 … (3.6.25)
Заметим, что значению m = 0 соответствует минимум темного пятна (не кольца). Аналогичный расчет можно провести и для светлых колец.
Если линзу постепенно отодвигать от поверхности пластинки, то интерференционные кольца будут стягиваться к центру: это ведь кольца (полосы) равной толщины, а она при этом перемещается к центру.
С помощью колец Ньютона можно с достаточно высокой точностью контролировать качество изготовления, например, сферических поверхностей.
Просветление оптики. В ее основе лежит интерференция света при отражении от тонких пластинок, дело в том, что при прохождении света через каждую преломляющую поверхность линзы отражается примерно 4% падающего света. В сложных объективах такие отражения совершаются многократно, и суммарная потеря светового потока оказывается весьма ощутимой. Например, в призменном бинокле она оставляет свыше 50%.
В просветленной оптике на каждую поверхность линзы наносят путем напыления тонкую пленку прозрачного диэлектрика с показателем преломления 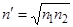 , где n1 и n2 — показатели преломления сред, между которыми находится пленка. При этом условии амплитуды отраженных от обеих поверхностей пленки волн оказываются, согласно (3.3.37), практически одинаковыми. Толщина же пленки делается такой, чтобы волны, отраженные от обеих поверхностей пленки, оказывались в противофазе, т. е. гасили друг друга.
, где n1 и n2 — показатели преломления сред, между которыми находится пленка. При этом условии амплитуды отраженных от обеих поверхностей пленки волн оказываются, согласно (3.3.37), практически одинаковыми. Толщина же пленки делается такой, чтобы волны, отраженные от обеих поверхностей пленки, оказывались в противофазе, т. е. гасили друг друга.
Обычно просветление оптики проводят для средней (желто-зеленой) области видимого спектра. Для краев же этого спектра коэффициент отражения заметно отличается от нуля, и объективы кажутся в отраженном свете пурпурными, что соответствует смешению красного и фиолетового цветов.
Лекция 3.7
Дата добавления: 2016-02-04; просмотров: 3090;