Построение дифракционной картины

Для того чтобы представить, как пойдут рентгеновские лучи после дифракции на неподвижном монокристалле, воспользуемся построением обратной решетки и сферы Эвальда (рис.4.1). Обратная решетка кристалла в данном случае неподвижна. Отражения будут давать те плоскости, одноименные узлы обратной решетки которых попадут на сферу отражения. Максимальный радиус сферы отражения будет отвечать l_min и равен R_max=1/l_min. Минимальный радиус сферы отражения будет равен R_min=1/l_max

.

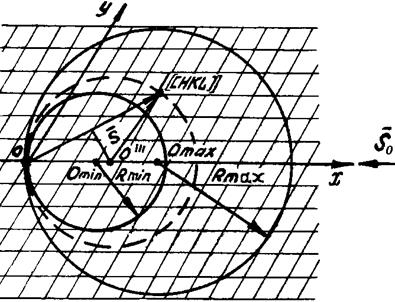
Рис.4.1. Построение дифракционной картины при съемке по Лауэ.

Между сферами с 1/l_min и 1/l_max ,будут располагаться непрерывным набором промежуточные сферы отражения, каждая из которых соответствует определенной длине волны l_min< l <l_max. Таким образом, отражения дадут все те плоскости кристалла, для которых узлы обратной решетки располагаются в промежутке между сферами с R_min и R_max или на их поверхности. Каждый такой узел попадет на какую-либо сферу отражения.

Рассмотрим, например, узел [[HKL]], находящийся в области отражений. Очевидно, соответствующая ему плоскость в кристалле дает отражение, т.к. узел [[HKL]] попадает на поверхность одной из промежуточных сфер.

Определим положение этой сферы в обратной решетке и направление отраженных от плоскости (HKL) лучей. Центр сферы легко определяетсяпри учете того обстоятельства, что на ее поверхности лежит как узел [[HKL]], так и точка 0 (начало координат обратной решетки). Для определения центра проводим вектор H_HKL и восстанавливаем к его середине перпендикуляр. Последний пересечется с направлением рентгеновского луча в точке 0¢¢¢. Эта точка и будет центром промежуточной сферы отражения, на которой находится узел [[HKL]]. Направление отраженного луча от плоскости (HKL) будет тогда определяться вектором S, проведенным из 0¢¢¢ в узел [[HKL]]. Проведя аналогичное построение для всех остальных узлов в области отражения, мы получим ряд дискретных направлений отраженных лучей. При пересечении с плоской фотопленкой они дадут на ней точки. Действительно, типичные рентгенограммы, снятые таким методом, состоят из точечных рефлексов(рис.4.2).

Рис.4.2. Схемы лауэграмм (а) и эпиграмм (б).

Как видно из рисунка, точки на рентгенограмме располагаются вдоль определенных кривых: эллипсов, парабол и гипербол. Можно показать, что каждая такая кривая объединяет точки, которые являются отражениями от плоскостей одной зоны (рис.4.3). Пусть NON¢ является осью некоторой зоны. Возьмем одну из плоскостей этой зоны (hkl). Это отражающая плоскость, S₀ – падающий луч, а S – отраженный. Проведем через S₀, S и нормаль H_hkl плоскость K, перпендикулярно к (hkl). Угол падения равен углу отражения, т.е. ÐS₀OC=ÐSOD=q (в плоскости K), а ÐСОE=ÐFOD=a(в плоскости hkl) и так как двугранный угол между плоскостями К и (hkl) прямой, то, очевидно, что ÐS₀ON=ÐSON¢=b.

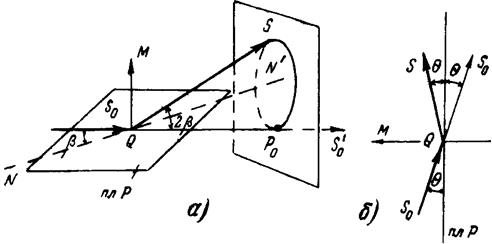
Рис.4.3. Геометрия съемки лауэграммы.

Теперь рассмотрим ход лучей, отраженных от всех плоскостей зоны. Отражение от плоскостей зоны с осью NN¢ можно заменить условно отражением от плоскости (hkl), которая вращается вокруг оси зоны. При этом как бы мы не поворачивали плоскость (hkl) ось зоны NN¢ остается на месте и угол b между падающим лучем и осью зоны остается тем же. Поскольку мы показали, что угол между отраженным лучом и осью зоны также равен b, то, следовательно, луч S, отраженный вращающейся плоскостью, сохраняет постоянный наклон к оси зоны и описывает конус с углом при вершине 2b. Как видно из рис.4.3,а, одна из образующих этого конуса является продолжением первичного пучка. Другими образующими конуса являются лучи, отраженные от плоскостей зоны. Поскольку в действительности число плоскостей зоны, имеющих возможность отражать лучи, ограничено и они повернуты на конечные углы относительно друг друга, то вместо сплошного эллипса на пленке мы имеем ряд пятен, расположенных по эллипсу.

Когда фотопластинка ставится за образцом, то на рентгеновскую пленку попадают лишь те отражения, для которых 2b<90° (рис.4.3,а). Если эллипс мал, значит ось, отвечающей ему зоны, близка к первичному лучу. Чем больше угол между осью зоны и первичным пучком, тем больше размер эллипса. Когда ось зоны образует угол в 45° с первичным пучком, угол раствора конуса равен 90° и пленка режет его параллельно одной из образующих. Линия пересечения является параболой. При углах наклона более 45°, конус пересекается с пленкой по гиперболе. Наконец, когда ось зоны перпендикулярна лучу, гипербола превращается в прямую, проходящую через центральное пятно.

Если рентгеновскую пленку поместить перед кристаллом, то мы будем фиксировать отражения для углов 2/3>90° (рис.4.4). Такие конусы пересекаются с плоскостью пленки по гиперболам (рис.4.2,б).

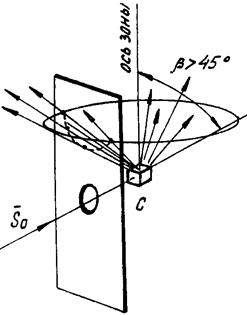
Рис.4.4. Геометрия съемки эпиграммы.

Итак, все отражения от плоскостей монокристалла при съемке его по методу Лауэ дают на плоской рентгеновской пленке, во-первых, точечные рефлексы и, во-вторых, отражения от плоскостей одной зоны в кристалле располагаются вдоль зональных кривых – эллипсов, парабол и гипербол. Схема съемки кристалла по методу Лауэ приведена на рис.4.5.

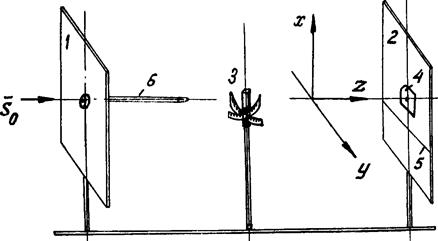
Рис.4.5. Схема камеры Лауэ.

Кристалл (3) при съемке по Лауэ устанавливается в гониометрической головке. Рентгеновский луч S₀ проходит через диафрагму (6) и при отражении от кристалла дает пучок дифракции, который может быть зафиксирован на двух плоских кассетах 1 (съемка на отражение) и 2 (съемка на просвет). В последнем случае для ослабления проходящего рентгеновского пучка фотопленка защищена в центре свинцовой пластиной (4). Нить (5) натягивается для определения положения внешней оси Y на фотопленке. X и Z – две другие ортогональные оси.