Понятие обратной решетки

В рентгеновской кристаллографии и квантовой теории металлов широко используется представление об обратной решетке. Она является математическим построением. Каждый узел обратной решетки отвечает определенной атомной плоскости пространственной решетки кристалла. Так, плоскости (hkl) прямой решетки в обратной решетке соответствует узел [[hkl]] с теми же индексами. При построении обратной решетки ее координатные оси и единичные вектора выбирают таким образом, чтобы выполнялись соотношения:

(aa*)=(bb*)=(cc*) = 1 , (1.24)

(ab*)=(ac*)=(ba*)=(bc*)=(ca*)=(cb*) = 0 , (1.25)

т.е. скалярные произведения одноименных векторов равны 1, а разноименных векторов – нулю. Здесь a, b, c – единичные вектора прямой решетки, a*, b*, c* – единичные вектора обратной решетки на координатных осях обратной решетки x*, y*, z*.

При таком построении, как будет показано ниже, обратная решетка очень наглядно характеризует расположение атомных плоскостей в прямой решетке и, кроме того, облегчает решение ряда структурных задач.

Из указанных соотношений вытекает ряд следствий, которые определяют направление координатных осей x*, y*, z* обратной решетки и величину единичных векторов a*, b*, c*.

Например, из соотношения (ba*) = 0 и (ca*) = 0 следует, что вектор a*обратной решетки перпендикулярен векторам b и с прямой и, следовательно, является нормалью к плоскости прямой решетки, в которой лежат эти вектора. Точно так же можно получить, что вектора b* и с* перпендикулярны плоскостям ac и ab прямой решетки, то есть все координатные оси обратной решетки перпендикулярны плоскостям прямой.

Величина единичных векторов обратной решетки может быть определена следующим образом. Поскольку вектор a* перпендикулярен плоскости bc, то его можно выразить через векторное произведение a*=j₁[bc], где j₁ - коэффициент пропорциональности и

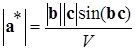
Умножим левую и правую части равенства наa, получим 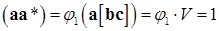, откуда .

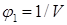Следовательно: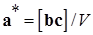

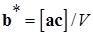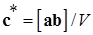и аналогично и (1.26)

Соотношение (1.26) позволяют определить величину единичных векторов обратной решетки. Обратная решетка является таким преобразованием прямой, при котором сохраняется ее сингония. Элементарная ячейка обратной решетки может иметь иное расположение узлов, чем у прямой решетки. Например, решетка обратная гранецентрированной кубической, есть кубическая объемноцентрированная.

Ориентацию плоскости (hkl) прямой решетки в пространстве определяет ориентацию вектора, соединяющего начало координат обратной решетки с ее узлом [[hkl]]. Такой вектор определяется соотношением

H = ha* + kb*+ lc* (1.27)

Докажем, что вектор H всегда перпендикулярен атомной плоскости прямой решетки с теми же индексами (hkl). Возьмем произвольную прямую решетку с осями координат x, y, z (рис.1.14). Выберем из семейства параллельных плоскостей (hkl) одну плоскость, ближайшую к началу координат. Эта плоскость отсекает отрезки на осях координат

OA=a/h; OB=b/k;OC=c/l (1.28)

Рассмотрим, что из себя представляет нормаль к плоскости (hkl). Очевидно, что направление нормали к плоскости должно быть параллельно векторному произведению двух векторов, лежащих в плоскости, например, произведению [AB×BC]. Подставим значение векторов из (1.28) и перемножим:

.

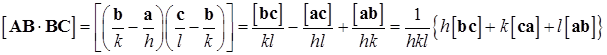Направление вектора не изменится, если умножим его на число 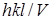, тогда

,

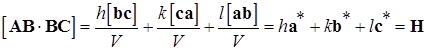т.е. векторное произведение [AB×BC] есть не что иное, как вектор Hобратной решетки, и он всегда перпендикулярен плоскости прямой решетки с теми же индексами.

Таким образом, зная направление вектора H,можно установитьориентацию в пространстве кристаллографической плоскости (hkl).

Величина вектора H. Абсолютное значение вектора H можно получить, рассматривая скалярное произведение вектора а/h и единичного вектораn вдоль оси N (рис.1.14). Последний равенn=H/|H|. Тогда скалярное произведение двух векторов можно записать, как произведение модуля одного из них |n| на алгебраическую проекцию другого вектораa/h на ось N. Поскольку алгебраическая проекция вектора a/h на ось N есть не что иное, как межплоскостное расстояние d, то имеем (n×a/ h) = 1×d или

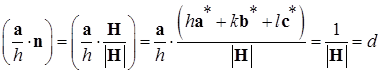(1.28)

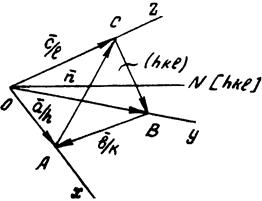
Рис. 1.14. К доказательству перпендикулярности вектора обратной решетки и плоскости прямой решетки (hkl).

Полученное соотношение (1.28) связывает величину вектора Hи межплоскостное расстояние. Используя это соотношение, можно получить квадратичные зависимости между величиной d, параметрами элементарной ячейки и индексами данной системы параллельных плоскостей. Рассмотрим несколько примеров.

Кубическая сингония. Запишем абсолютное значение H как

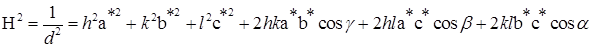(1.29)

В конечном итоге можно дать следующее определение обратной решетки: обратной решеткой называется совокупность узлов, связанных с совокупностью нормалей H_hkl к плоскостям прямой решетки. Узел обратной решетки представляет собой конец нормали, проведенной из начала координат прямой решетки и имеющий длину H, обратно пропорциональную соответствующему межплоскостному расстоянию системы плоскостей (hkl) в прямой решетке. Такая совокупность узлов образует обратную пространственную решетку.