Кристаллографические проекции

При графическом изображении кристаллов широко пользуются различными их проекциями. Проекции применяются для решения ряда задач кристаллографии и рентгеноструктурного анализа: определения ориентировки кристаллов, индицирования рентгенограмм и т.д. Обычно ими пользуются тогда, когда нет необходимости определять межплоскостные расстояния, а требуется установить лишь взаимную ориентацию атомных плоскостей, граней и ребер кристалла. Поскольку расстояния между параллельными плоскостями кристалла равны, то всю совокупность параллельных плоскостей при построении проекций заменяют одной плоскостью, а все параллельные прямые – одной прямой.

В целом весь проектируемый кристалл заменяется пучком прямых и плоскостей, проходящих через одну точку. Полученное построение называют кристаллическим комплексом.

Таким образом, кристаллический комплекс – это совокупность прямых и плоскостей, параллельных ребрам и граням кристалла, проходящих через одну точку. Эта точка называется центром комплекса.

При проектировании кристаллического комплекса на плоскость получают линейную проекцию кристалла; при проектировании на сферу – сферическую. На линейной проекции плоскость изобразится прямой, являющейся ее следом; прямая – точкой. Неудобство этой проекции состоит в том, что для изображения всех плоскостей и прямых необходима бесконечно большая плоскость проекций. Поэтому линейная проекция применяется очень редко.

При построении сферической проекции центр сферы совмещается с центром комплекса. Очевидно, на сферической поверхности все плоскости кристаллического комплекса проектируются в виде больших кругов, стягиваемых сферой, прямые – двумя диаметрально противоположными точками. Неудобством сферической проекции при большом числе проектируемых плоскостей является сложность и громоздкость построения.

В кристаллографии, при решении многих задач, пользуются преимущественно обратным кристаллографическим комплексом, в котором плоскости заменяют нормалями к ним, а прямые – перпендикулярными к ним плоскостями. Полученная совокупность прямых и плоскостей, проходящих через одну точку 0, и носит название обратного или полярного комплекса. Точка 0 – центр комплекса.

Все проекции, полученные при проектировании полярного комплекса, имеют приставку “гномо”. Проекция полярного комплекса на плоскость носит название гномонической проекции. Плоскость (hkl) в ней изобразится точкой. Недостаток этой проекции тот же, что и у линейной, а именно для построения всей совокупности проекций плоскостей требуется очень большая площадь проекций. Чтобы устранить этот недостаток, плоскость проекций заменяют сферой. В результате получаем гномосферические проекции.

Проекцией плоскости (hkl) здесь будет точка пересечения M нормали со сферой. Положение точки M на сфере описывается в кристаллографии, выраженными в градусах: полярным расстоянием r, и долготой j. Полярное расстояние или широта отсчитывается обычно от полюса и меняется в пределах от 0 до 180° градусов.

Долготу отсчитывают от некоторого начального меридиана от 0 до 360° градусов по часовой стрелке, если смотреть с верхнего полюса.

Недостаток гномосферической проекции состоит в том, что определение положения точек на сфере проекций и решение ряда задач связано с гониометрическими измерениями (на сфере). Это неудобно.

Наиболее часто в кристаллографии пользуются гномостереографическими проекциями. Они включают в себя достоинства, свойственные линейным и гномоническим проекциям, а именно: комплекс проектируется на плоскость, которая ограничена кругом проекций. Здесь так же, как и в предыдущих случаях, центр полярного комплекса совмещается с центром сферы(рис.1.16). Через центр сферы проводится плоскость проекции P, которая пересекает сферу по большому кругу. Это сечение называется основным кругом проекции.

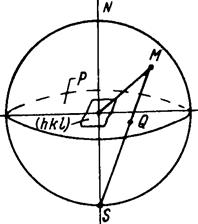
Рис.1.16. Гномостереографическая проекция.

Прямая, перпендикулярная к плоскости P и проходящая через центр О, пересекает сферу в двух точках N и S, которые называют полюсами проекций. При построении гномостереографической проекции плоскости (hkl) точку выхода ее нормали на сфере (точку M) соединяют с полюсом проекций, расположенным по другую сторону от плоскости Р. Точка пересечения прямой MS с плоскостью P (точка Q) и будет являться гномостереографической проекцией плоскости (hkl).

Легко видеть, что проекции всех плоскостей кристалла находятся в пределах большего круга. Таким образом, размеры проекции конечны и определяются радиусом сферы. В этом одно из достоинств гномостереографической проекции.

Построение гномостереографической проекции кристалла проводят, взяв только один из полюсов проекции, например S, и рассматривая нормали, направленные в одну сторону от плоскости проекций P. Тогда для каждой плоскости (hkl) получаем одну точку проекции (hkl), которую называют полюсом плоскости. Совокупность гномостереографических проекций плоскостей кристалла на большом круге проекций называется его полюсной фигурой (рис.1.17).

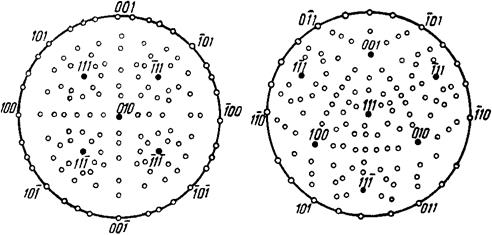
Рис. 1.17. Полюсные фигуры.

Вид полюсной фигуры зависит от симметрии кристалла, а также от его установки относительно плоскости проекций и прямой SN. При изменении установки кристалла все точки проекций на полюсной фигуре смещаются.

Плоскость или грань кристалла, перпендикулярная прямой SN, будет иметь проекцию в центре большого круга; все плоскости, параллельные прямой SN, спроектируются в виде точек на большом круге проекций. Все другие плоскости кристалла дадут точки проекций на остальной площади большего круга.

Рассмотрим, как будут располагаться на полюсной фигуре точки гномостереографической проекции какой-либо кристаллографической зоны (рис.1.18).

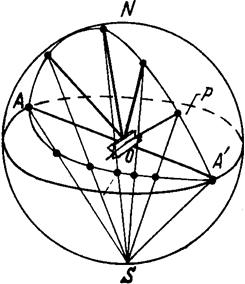
Рис. 1.18. Гномостереографическая проекция плоскостей одной зоны.

Для этого представим зону в виде полярного комплекса, выбрав за центр комплекса некоторую точку на оси зоны. В полярном комплексе зона изобразится в виде прямых – нормалей, лежащих в одной плоскости (рис.1.18), перпендикулярной оси зоны. Эта плоскость пересечет сферу по большому кругу, следовательно, выходы всех нормалей к плоскостям зоны будут также располагаться на большем круге сферы проекций.

Гномостереографической проекцией большого круга будет дуга, стягиваемая диаметром A¢A (рис.1.18). Таким образом, все точки проекций плоскостей одной кристаллографической зоны будут располагаться по дуге, стягиваемой на концах диаметром круга проекций. Если ось зоны совпадает с направлением SN, то ее проекция будет представлять собой ряд точек, расположенных по периметру большого круга проекций P. На рис.1.18 ось зоны не совпадает с направлением SN, а составляет с ней угол 90°. Индексы оси этой зоны для кубического кристалла совпадают с индексами центральной точки полюсной фигуры.