Нуль-граф и полный граф
Существуют некоторые специальные графы, встречающиеся во многих приложениях теории графов. Будем пока опять рассматривать граф как наглядную схему,иллюстрирующую ход спортивных состязаний. Доначала сезона, пока еще никакие игры не проводились, на графе нет никаких ребер. Такой граф состоит из одних изолированных вершин, т. е. извершин, не соединенных никакими ребрами. Граф такого вида называется нуль-графом. На рис. 3приведены такие графы для случаев, когда число команд, или вершин, равно 1, 2, 3, 4 и 5. Эти нуль-графы обычно обозначаются символами O1, O2,O3и т. д., такчто On – это нуль-граф с n вершинами, не имеющий ребер.
Рассмотрим другой крайний случай. Предположим,что по окончании сезона каждая команда сыграла по одному разу с каждой из остальных команд. Тогда на соответствующем графе каждая пара вершин будет соединена ребром. Такой граф называется полнымграфом. На рис. 4 изображены полные графы с числом вершин n = l, 2, 3, 4, 5.

Рис. 3. Нуль-графы для различного числа команд: 1,2,3,4 и 5
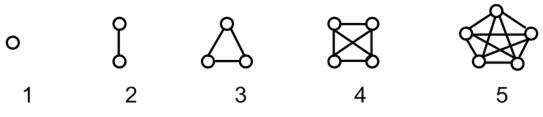
Рис. 4. Полные графы для различного числа команд: 1,2,3,4 и 5
Обозначим этиполные графы соответственно через U1, U2, U3, U4, U5, так что граф Un состоит из n вершин и ребер, соединяющих все возможные пары этих вершин. Этот граф можно представлять себе как n -угольник, в котором проведены все диагонали.
Имея некоторый граф, например граф G, изображенный на рис. 1, всегда можно превратить его в полный граф с теми же самыми вершинами, добавив недостающие ребра (т. е. ребра, соответствующие играм, которые только еще будут сыграны). На рис. 5 это сделано для графа, представленного на рис. 1 (еще не состоявшиеся игры изображены пунктиром).
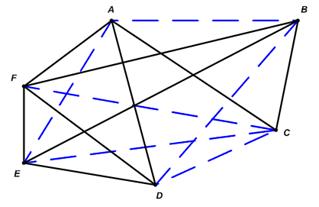
Рис. 5. Граф с рис. 1, дополненный ребрами до полного графа
Можно также отдельно начертить граф, соответствующий пока еще не сыгранным, будущим играм. Для графа G при этом получится граф, изображенный на рис. 6.
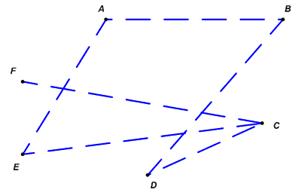
Рис. 6. Граф 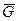 , являющийся дополнением графа G с рис. 1 до полного графа
, являющийся дополнением графа G с рис. 1 до полного графа
Этот новый граф называется дополнениемграфа G; принято обозначать его через 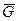 . Взяв дополнение графа
. Взяв дополнение графа 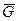 , мы снова получим граф G. Ребра обоих графов G и
, мы снова получим граф G. Ребра обоих графов G и 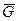 вместе составляют полный граф с теми же вершинами.
вместе составляют полный граф с теми же вершинами.
Упражнения
1. Начертите дополнение графа, изображенного на рис. 2.
2. Чему равно число ребер полного графа Un?
Изоморфные графы
Граф G (рис. 1) можно изображать по-разному. Во-первых, не обязательно изображать его ребра прямолинейными. Можно провести любые линии, соединяющие те же самые вершины, что ираньше, так что граф G можно представить в виде, изображенном на рис. 7.
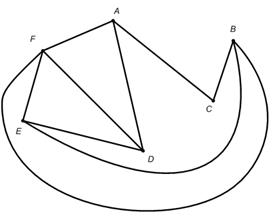
Рис. 7. Граф G1, изоморфный графу G, изображенному на рис. 1
Во-вторых, можно произвольно располагать вершины на плоскости. Например, вершины графа Gможно расположить так, как показано на рис.8.
Если рассматривать три графа, изображенные нарис. 1, 7 и 8, как графы, описывающие ход спортивного турнира, то они будут содержать в точности одну и ту же информацию относительно того, какие именно команды уже играли друг с другом; в некотором смысле это один и тот же граф. Мы будем говорить, что два графа – обозначим их G1 и G2 – изоморфны, если они отвечают одному и тому же списку проведенных игр. Иными словами, если графы G1 и G2 изоморфны, то они имеют одно и то же число вершин и для любых двух вершин графа G1 , скажем В1 и С1, соединенных ребром, соответствующие им вершины В2 и С2 графа G2 тоже соединены ребром, и обратно.
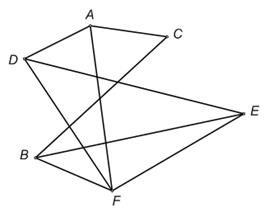
Рис. 8. Граф G2, изоморфный графу G, изображенному на рис. 1 и графу G1, изображенному на рис. 7
Согласно этому определению, три графа на рис. 1, 7 и 8 изоморфны (т. е. имеют одно и то же строение), хотя они и выглядят по-разному. (Термин «изоморфный» часто используется в математике; он состоит из греческих слов ιζωσ (isos) – равный, одинаковый и μορφε (morphē) – вид, форма).
Нередко приходится решать вопрос о том, являются ли два данных графа изоморфными. Иногда сразу ясно, что это не так. Например, графы, изображенные на рис. 9, не могут быть изоморфными, потому что они имеют неодинаковое число вершин.
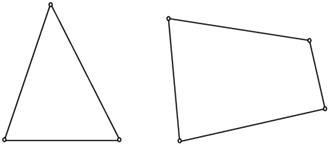
Рис. 9. Пример неизоморфных графов
Не могут быть изоморфными и графы рис. 10, так как у них неодинаковое число ребер.
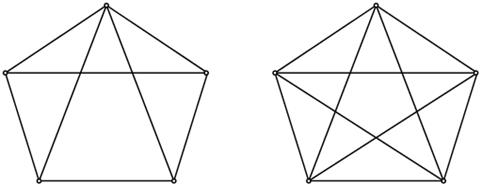
Рис. 10. Пример неизоморфных графов
Однако для того, чтобы показать, что не изоморфны графы, изображенные на рис. 11, требуется уже несколько более тонкое рассуждение.
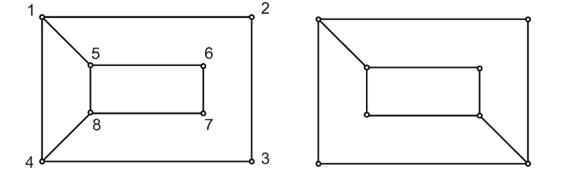
Рис. 11. Менее очевидный пример неизоморфных графов
Так, можно заметить, что на первом графе имеется последовательность из восьми смежных ребер (т. е. ребер, попарно имеющих общую вершину):
(1,2), (2,3), (3,4), (4,8), (8,7), (7,6), (6,5), (5,1),
возвращающаяся к исходной вершине, в то время как на втором графе такой последовательности нет. Значит, как бы ни были обозначены вершины второго графа, невозможно для каждой пары соединенных ребром вершин одного графа указать во втором соответствующую пару вершин, тоже соединенных ребром. (Докажите это!)
Если сразу не видно, как доказать, что два графа не изоморфны, то вопрос об их изоморфности может оказаться довольно трудным.
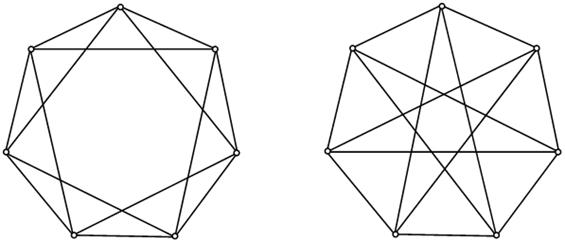
Рис. 12. Пример неочевидного изоморфизма графов
В качестве примера рассмотрим два графа, изображенных на рис. 12; эти графы на самом деле изоморфны.
Упражнения
1. Покажите, что графы, изображенные на рис. 1, 2, 6, не изоморфны между собой.
2. Укажите еще одну причину, в силу которой два графа рис. 11 не могут быть изоморфными.
3. Обозначьте вершины двухграфов рис. 12 так, чтобы изоморфность этих графов стала очевидной.
Плоские графы
Для многих целей безразлично, как именно изображен граф, т. е. изоморфные графы, доставляющие одну и ту же информацию, могут рассматриваться как один граф. Так будет, например, в том случае, с которого начато изложение, – когда граф играет роль своеобразного списка уже проведенных игр. Однако в других случаях существенно то обстоятельство, что граф может быть начерчен некоторым специальным образом. Сравним два изоморфных графа, изображенные на рис. 1 и 7. На первом из них ребра пересекаются в пяти точках, не являющихся вершинами графа, на втором все точки пересечения ребер графа служат его вершинами.
Граф, который можно начертить таким образом, чтобы его ребра пересекались только в вершинах, называется плоскимграфом. Так, граф G, изображенный на рис. 1, является плоским, потому что существует изоморфный ему граф (рис. 7), все ребра которого пересекаются только в вершинах.
Плоский граф можно рассматривать как карту дорог, соединяющих между собой различные станции или деревни. Так, на карте, изображенной на рис. 13, мы видим 7 станций: А, В, ..., G, причем некоторые из них соединены друг с другом дорогами: АG, ВС, FE и т. д., и обратно, каждую карту дорог можно рассматривать как плоский граф. План любого города тоже является плоским графом, где улицы служат ребрами, а площади и уличные перекрестки – вершинами.
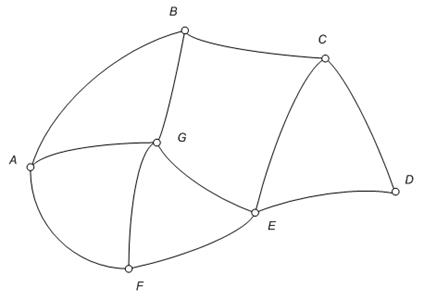
Рис. 13. Граф, соответствующий карте дорог, соединяющих семь станций
Впрочем, современная техника изменила многие наши представления, и, чтобы не отстать от современных требований, необходимо признать, что и карта дорог в настоящее время уже не всегда представляетсяплоским графом. К сети дорог теперь часто добавляются линии, проходящие на разных уровнях (дорожные развязки), так что в месте пересечения двух дорог пассажир не может перейти с одной линии на другую (рис. 14).

Рис. 14. Фотография современной многоуровневой дорожной развязки, которую невозможно представить плоским графом
Иными словами, ребра графа такой карты пересекаются в точках, которые нельзя считать вершинами графа.
Планарнымназывается граф, изоморфный плоскому графу. Иначе говоря, граф планарный, если существует возможность получения плоской укладки такого графа.
В дополнение к перечисленным выше представлениям графа укажем еще одно приложение плоских графов к важной задаче практики: его можно рассматривать как схему электрической сети, где ребрами служат провода, соединяющие различные пункты. Один из наиболее эффективных способов массового производства стандартных электрических схем для радио- и телевизионных приемников состоит в том, что схема наносится печатным способом в виде металлической фольги на бумажную или пластмассовую основу. Однако для того, чтобы это было осуществимо, граф рассматриваемой сети проводов должен иметь плоское представление; ведь пересечение двух ребер привело бы к короткому замыканию в системе.
Упражнения
1. Нарисуйте плоский граф, отвечающий сети дорог некоторой окрестности того места, где вы живете.
2. Сделайте то же самое, используя план вашего или другого города.
Число ребер графа
Когда мы ввели понятие графа как своего рода списка уже проведенных игр, мы предполагали, что каждые две команды играют друг с другом, самое большее, по одному разу. Может, однако, случиться, что каждые две команды играют между собой и по нескольку игр, как это бывает, например, в футболе. Мы можем отразить это на графе, соединяя соответствующие пары вершин несколькими ребрами (рис. 15). В этом случае говорят, что граф имеет кратные ребра.
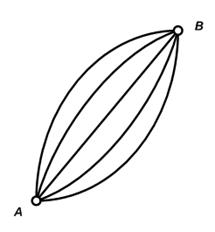
Рис. 15. Граф с 5 кратными ребрами
Вместо того чтобы на самом деле проводить несколько ребер между одними и теми же вершинами А и В, можно провести всего одно ребро, приписав ему кратность, показывающую сколько раз надо считать это ребро (рис. 16). На карте дорог, конечно, проводят каждую дорогу в отдельности.
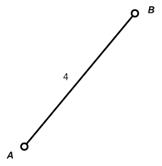
Рис. 16. Экономичное изображение графа с ребром кратности 4
В каждой неизолированной вершине А некоторого графа G имеется одно или несколько ребер, для которых А служит концом; все эти ребра называются инцидентными вершине А. Число таких ребер обычно обозначают через р(А) и называют степенью вершины А.
Так, для графа G, изображенного на рис. 1, степени вершин таковы:
p(A)=p(B)=p(D)=p(E)=3; p(F)=4, р(С)=2.
Довольно часто приходится находить число ребер графа. Их можно, конечно, пересчитать непосредственно, но проще сосчитать число ребер в каждой вершине отдельно и сложить все эти числа. При этом каждое ребро будет сосчитано дважды — соответственно двум вершинам, которые оно соединяет, поэтому общее число ребер графа будет равно половине этой суммы. Так, например, число ребер графа G с рис. 1 равно
½[р (А)+ р (В)+р (С)+ р (В)+ р(Е)+ р (Р)] = 9.
Чтобы сформулировать соответствующий результат в общем виде, предположим, что некоторый граф G имеет n вершин
А1, А2..., Аn,
степени которых соответственно равны
р(А1), р(А2), ..., р(Аn).
Тогда число N ребер графа G, как показывает наше рассуждение, равно
N =1/2[р(А1)+р(А2)+ … +р(Аn)]. (1)
Из этой формулы видно, что для любого графа сумма степеней всех его вершин
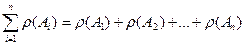 (2)
(2)
является числом четным, поскольку она равна удвоенному числу ребер.
На графе можно различать два типа вершин: нечетные вершиныА', степени р(А') которых нечетны, и четные вершиныА", имеющие четные степени р(А"). Так, в случае графа рис. 1 вершины А, В, D, Е являются нечетными, а вершины С и F четны. Если вершины расположить в алфавитном порядке, то сумма (2) будет равна
3+3+2+3+3+4=18.
Эта сумма четна, так как число ее нечетных слагаемых равно четырем. Вообще, для того чтобы узнать, будет ли сумма целых чисел четной или нечетной, мы можем не рассматривать четные слагаемые; сумма будет четной или нечетной в зависимости от четности или нечетности числа ее нечетных слагаемых. А так как сумма (2) всегда является четной, мы приходим к следующему результату.
Теорема 1. Число нечетных вершин любого графа четно.
Это утверждение справедливо и в случае, когда граф вовсе не содержит нечетных вершин, так как 0 является числом четным.
Бывают графы, у которых степени всех вершин одинаковы:
р(А1)=р(А2)= ... =р(Аn)=r.
Такой граф называется однородным графомстепени r; в силу формулы (1) число его ребер равно
N= (1/2) nr
где n – число вершин этого графа. Граф, изображенный на рис. 17 является однородным, его степень равна трем; граф, изображенный на рис. 18 также однородный, и его степень равна четырем.
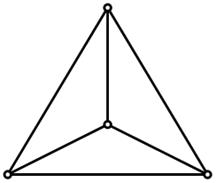
Рис. 17. Однородный граф степени r = 3
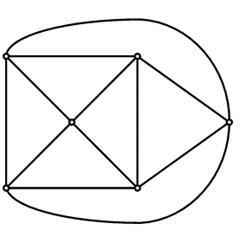
Рис. 18. Однородный граф степени r = 4
В полном графе Un с n вершинами из каждой вершины выходит n – 1 ребер, ведущих к каждой из остальных n – 1 вершин; таким образом, Un является однородным графомстепени n – 1. Нуль-граф 0 n тоже является однородным по той простой причине, что для каждой его вершины р(А)=0.
Упражнения
1. Проверьте формулу (1) для графов рис. 2 и 6.
2. Проверьте, что на каждом из этих графов число нечетных вершин четно.
Дата добавления: 2016-02-02; просмотров: 2145;
