Описание спортивных соревнований с помощью графов

Предположим, что футбольная команда вашего вуза участвует в соревнованиях и играет с командами других вузов. Пусть общее число команд равно шести. Вашу команду обозначим буквой А, а другие команды – буквами В, С, D, E и F. Через несколько недель после начала соревнований окажется, что некоторые из команд уже сыграли друг с другом, например:

А с С,D,F,

В с С, Е, F,

С с А, В,

D с А, Е,F,

Е с В,D,F,

F с А,В,D,Е.

Это можно изобразить при помощи такой геометрической схемы. Каждую команду представим точкой или маленьким кружочком и соединим отрезком те пары точек, которые соответствуют командам, уже игравшим друг с другом. Тогда для данного списка проведенных игр получим схему, изображенную на рис. 1.

Схема такого вида называется графом. Она состоит из нескольких точек А, В, С, D, Е, F, называемых вершинами, и нескольких соединяющих эти точки отрезков, таких как АС или ЕВ, называемых ребрамиграфа.

Из рис. 1 видно, что точки пересечения некоторых ребер графамогут не являться его вершинами; это происходит потому, что наш граф изображен на плоскости.

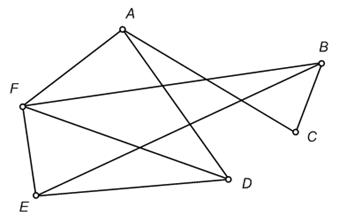
Рис. 1. Граф G сыгранных футбольных матчей в ходе соревнований

Возможно, удобнее было бы представлять себе его ребра нитями, проходящими друг над другом в пространстве. При изображении на плоскости вершины графа во избежание путаницы должны отмечаться достаточно отчетливо (например, кружочками).

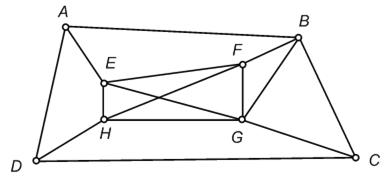
Рис. 2. Граф состязания восьми команд

Каждую совокупность игр любого турнира можно представить соответствующим графом. Наоборот, если задан некоторый граф, т. е. фигура, состоящая из точек – вершин, соединенных прямолинейными отрезками – ребрами, то его можно рассматривать как схему такого состязания. В качестве примера рассмотрим граф, изображенный на рис. 2. Его можно представлять себе как граф, соответствующий состязанию восьми команд, где команда А уже играла с командами В, Е, D, команда В играла с А, F, G, С и т. д.

Упражнения

1. Начертите граф игр, сыгранных к середине сезона вашими футбольными или волейбольными командами.

2. Дайте полный список проведенных игр, соответствующий графу рис. 2.

3. Сколько ребер и сколько вершин имеют графы рис. 1 и 2?