Функция распределения Пуассона
Функцияраспределения Пуассона задает вероятность прихода n заявок в интервале длительностью t в соответствии с выражением:
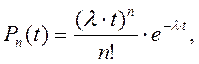
 где n ³ 0;
где n ³ 0;
λt – число заявок за время t, носит название параметра распределения.
На рис. 5.8 показаны кривые распределения Пуассона для разных значений n.
С математической точки зрения распределение Пуассона является дискретным многомерным распределением вероятностей.
Из рисунка 5.8 видно, что с увеличением интервала времени вероятность отсутствия заявки (n=0) только уменьшается, тогда как графики вероятностей прихода 1, 2, 3 и т.д. заявок (соответственно n =1,2,3 и т.д.) имеют максимумы. Это объясняется тем, что с увеличением временного интервала вначале вероятность поступления именно данного числа заявок возрастает, а затем начинает уменьшаться – за счет возрастания вероятности прихода большего (чем данное n) числа заявок.

Рис. 5.8. Функция распределения простейшего пуассоновского потока заявок
5.1.7. Характеристики обслуживания
1. Функция распределения времени обслуживания (интервала занятости) F*(t)
Характеризует процесс обслуживания заявок, поступающих в СМО. Задается конкретным выражением закона распределения, например, любого из приведенных в Приложении 3.
2. Плотность распределения времени обслуживания w*(t)
Эта характеристика (аналогично вышеупомянутой плотности из п.3) представляет собой производную по времени от функции распределения вероятности F*(t):
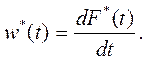

3. Среднее время обслуживания (интервала занятости):
Усредненная характеристика процесса обслуживания (аналогичная вышеупомянутому математическому ожиданию из п. 4).

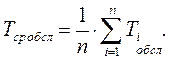
Дата добавления: 2016-02-02; просмотров: 858;
